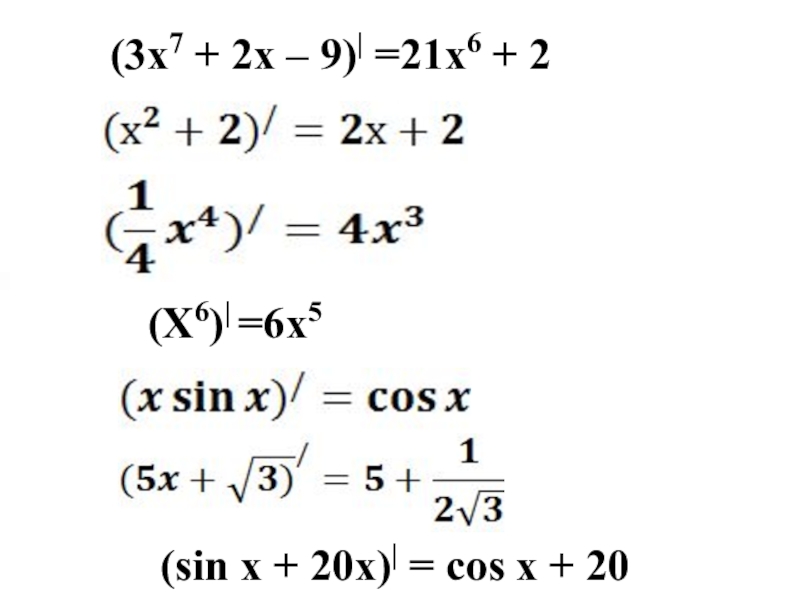- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Вычисление производной 10 класс
Содержание
- 1. Презентация Вычисление производной 10 класс
- 2. Кто? Что? Когда?
- 3. Этот математик пришел к открытию дифференциального исчисления
- 4. Готфрид Вильгельм Лейбниц(1646 – 1716)
- 5. Он пытался строить дифференциальное исчисление алгебраически, пользуясь
- 6. Жозеф Луи Лагранж(1736-1813)
- 7. Назовите ученого, который пришел к открытию дифференциального
- 8. Исаак Ньютон (1643-1727)
- 9. Лозунгом многих математиков XVII в. был: «Двигайтесь
- 10. Ответим на вопросы:Сформулировать понятие производной функции?2) Обозначение
- 11. Ответим на вопросы:4) В чем заключается геометрический
- 12. Слайд 12
- 13. Слайд 13
- 14. АКЦЕНТИРУЕМ ТЕОРИЮ ПО ТЕМЕГРАФИК1. В чем состоит
- 15. для дифференцируемых функций : 0° ≤ α
- 16. Задача 1.2. На рисунке изображен график функции
- 17. Вычисление производнойПроверь себя!Вперед!!!
- 18. Найдите производную следующей функции и выберите
- 19. Найдите производную следующей функции и выберите правильный
- 20. Найдите производную следующей функции и выберите правильный
- 21. Найдите производную следующей функции и выберите правильный
- 22. Подведем итоги: 1. с
- 23. 2. Чему равна производная в точке М
- 24. Индивидуальная работа по карточкамс взаимопроверкой
- 25. Ответы:
- 26. Электронные физминуткидля глаз
- 27. (3х7 + 2х – 9)| =21х6 +
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
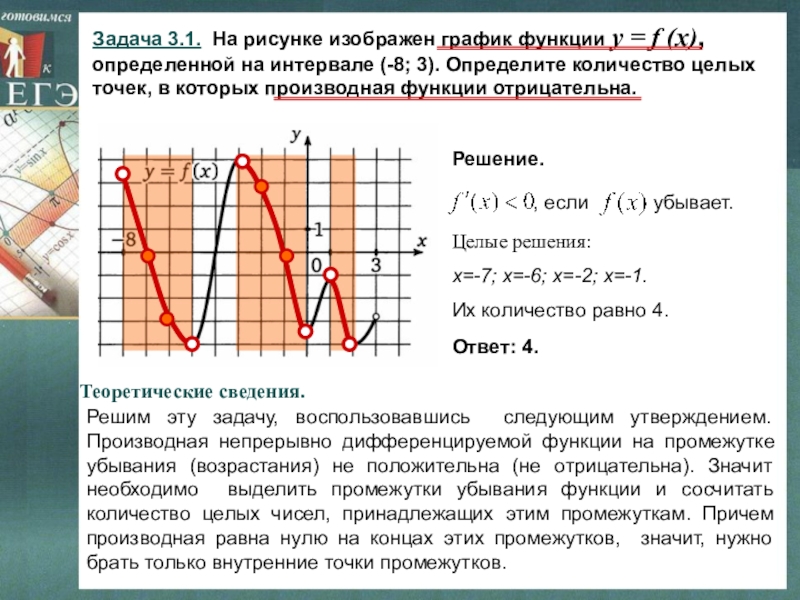
- 32. Задача 3.1. На рисунке изображен график функции
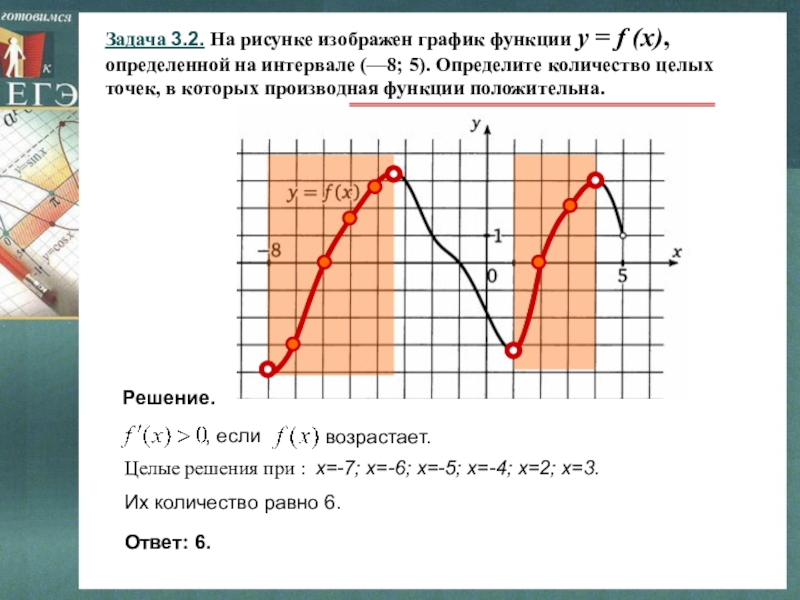
- 33. Задача 3.2. На рисунке изображен график функции
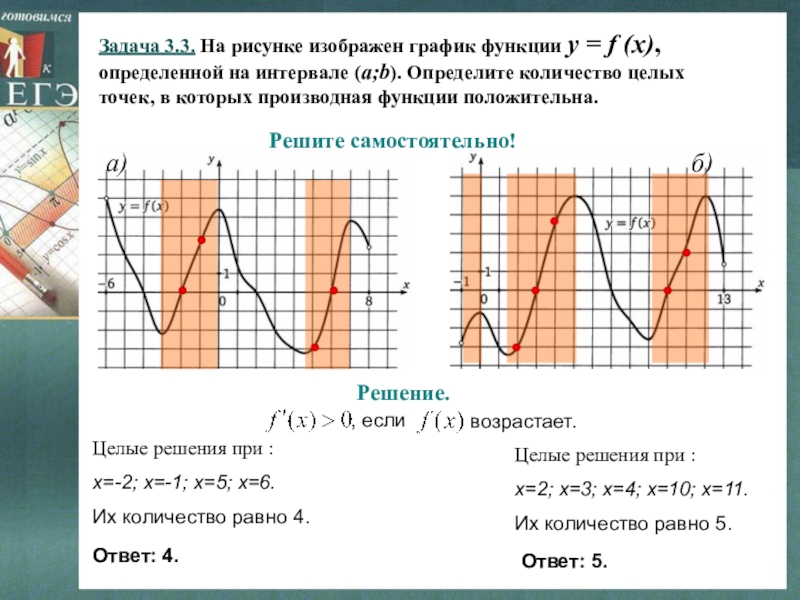
- 34. Задача 3.3. На рисунке изображен график функции
- 35. Рефлексия- Каким вопросам был посвящен урок?- Чему научились на уроке? -
- 36. Слайд 36
- 37. Найдите производные функций:Правильный ответПравильный ответПравильный ответПравильный ответПравильный ответ
- 38. Найдите производные функций:Правильный ответПравильный ответПравильный ответПравильный ответПравильный ответ
Слайд 3Этот математик пришел к открытию дифференциального исчисления при решении задач о
Слайд 5Он пытался строить дифференциальное исчисление алгебраически, пользуясь разложением функций в степенной
Слайд 7Назовите ученого, который пришел к открытию дифференциального исчисления при решении задач
Слайд 9Лозунгом многих математиков XVII в. был: «Двигайтесь вперёд, и вера в
Производная – одно из фундаментальных понятий математики, характеризующее скорость изменения функции в данной точке. Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий.
Слайд 10Ответим на вопросы:
Сформулировать понятие производной функции?
2) Обозначение производной
3) Как называется математическая
Ответ: Производной функции y = f(x) в данной точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.
Ответ: Операция нахождения производной называется дифференцированием.
Слайд 11Ответим на вопросы:
4) В чем заключается геометрический смысл производной функции?
5) В
4) Если функция непрерывна, то она дифференцированная и наоборот? Верно ли это утверждение?
Ответ: Если тело движется по прямой согласно закону s(t), то формулы для нахождения скорости и ускорения тела в момент времени t: v (t)= s‘(t) и а(t) = v’(t).
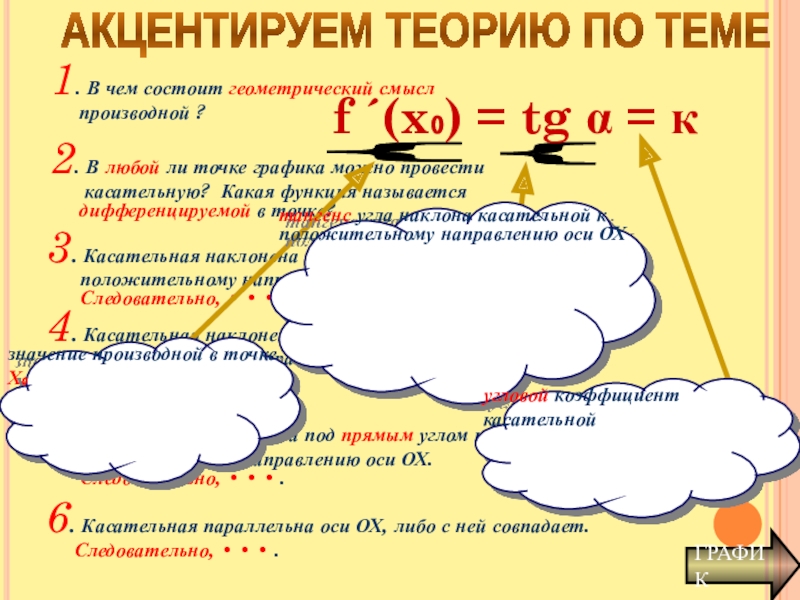
Слайд 14АКЦЕНТИРУЕМ ТЕОРИЮ ПО ТЕМЕ
ГРАФИК
1. В чем состоит геометрический смысл
2. В любой ли точке графика можно провести
касательную? Какая функция называется
дифференцируемой в точке?
3. Касательная наклонена под тупым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
4. Касательная наклонена под острым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
5. Касательная наклонена под прямым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
6. Касательная параллельна оси ОХ, либо с ней совпадает. Следовательно, • • • .
}
значение производной в точке Х₀
}
тангенс угла наклона касательной к положительному направлению оси ОХ
угловой коэффициент касательной
f ´(x₀) = tg α = к
Слайд 15для дифференцируемых функций : 0° ≤ α ˂180°, α ≠ 90°
вопросы
α
tg α < 0
f ´(x₀) < 0
α – острый
tg α >0
f ´(x₁) >0
α = 90°
tg α не сущ.
f ´(x₃) не сущ.
α = 0
tg α =0
f ´(x₂) = 0
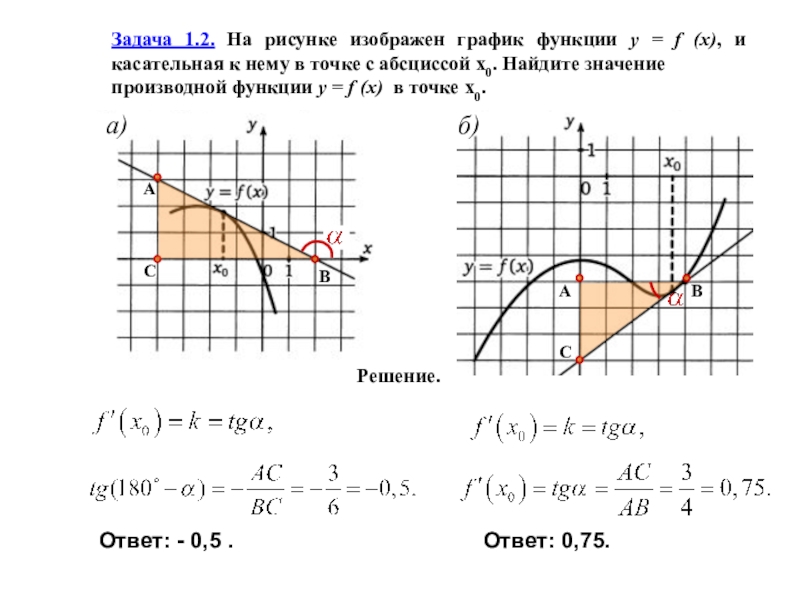
Слайд 16Задача 1.2. На рисунке изображен график функции y = f (x),
производной функции y = f (x) в точке х0.
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
С
В
А
a)
б)
Слайд 21Найдите производную следующей функции и выберите правильный ответ:
А теперь давай сравним ответы
Слайд 232. Чему равна производная
в точке М ?
М
Чему равен угловой
в точке М?
М
М
1
1
Определите по графику функции у = f (x):
подсказка
Слайд 32Задача 3.1. На рисунке изображен график функции y = f (x),
определенной на интервале (-8; 3). Определите количество целых точек, в которых производная функции отрицательна.
Решим эту задачу, воспользовавшись следующим утверждением. Производная непрерывно дифференцируемой функции на промежутке убывания (возрастания) не положительна (не отрицательна). Значит необходимо выделить промежутки убывания функции и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков.
Решение.
Целые решения:
х=-7; х=-6; х=-2; х=-1.
Их количество равно 4.
Ответ: 4.
Теоретические сведения.
Слайд 33Задача 3.2. На рисунке изображен график функции y = f (x),
Решение.
Целые решения при : х=-7; х=-6; х=-5; х=-4; х=2; х=3.
Их количество равно 6.
Ответ: 6.
Слайд 34Задача 3.3. На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых производная функции положительна.
a)
б)
Решите самостоятельно!
Решение.
Целые решения при :
х=-2; х=-1; х=5; х=6.
Их количество равно 4.
Целые решения при :
х=2; х=3; х=4; х=10; х=11.
Их количество равно 5.
Ответ: 4.
Ответ: 5.
Слайд 35Рефлексия
- Каким вопросам был посвящен урок?
- Чему научились на уроке?
- Какие теоретические факты обобщались
И, наконец, после “всяких умных вещей” немного юмора.