- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Вычисление площадей плоских фигур
Содержание
- 1. Презентация Вычисление площадей плоских фигур
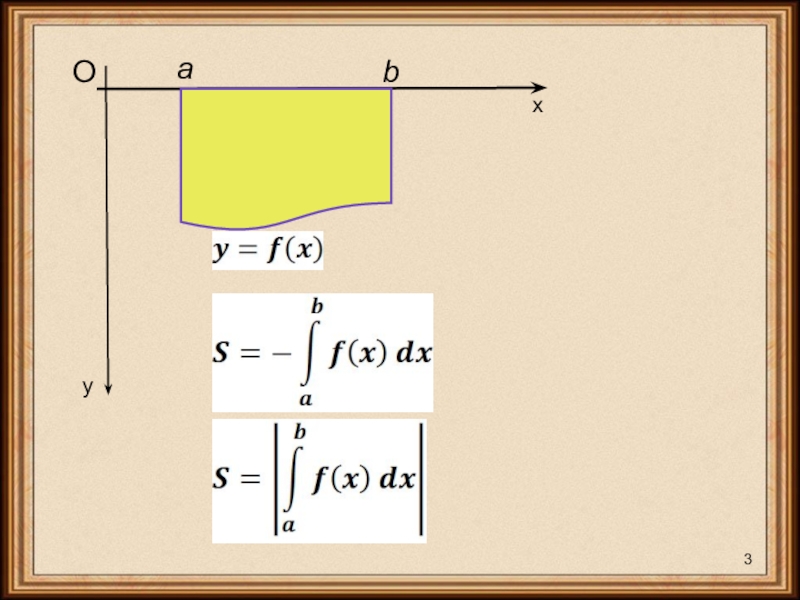
- 2. Пусть функция f(x)непрерывна и неотрицательна на отрезке [a;b]. Площадь криволинейной трапеции.S
- 3. xyOab
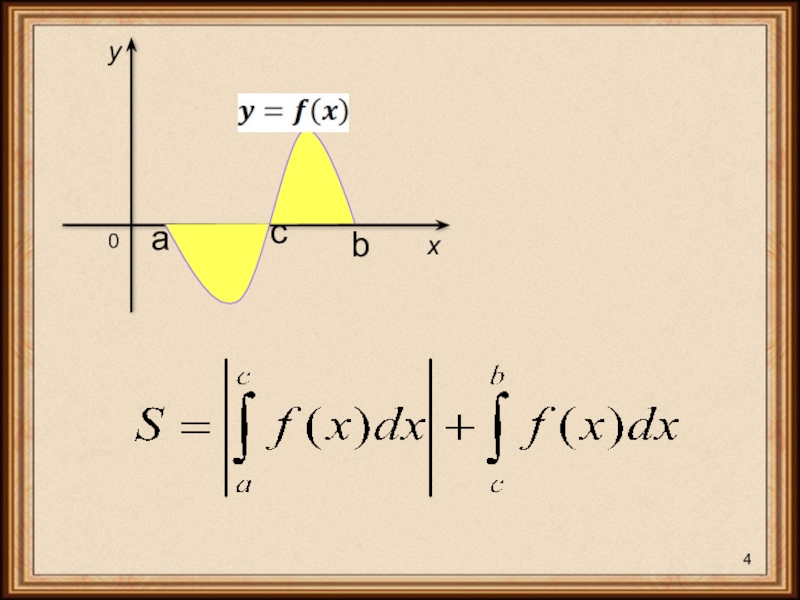
- 4. 0byxca
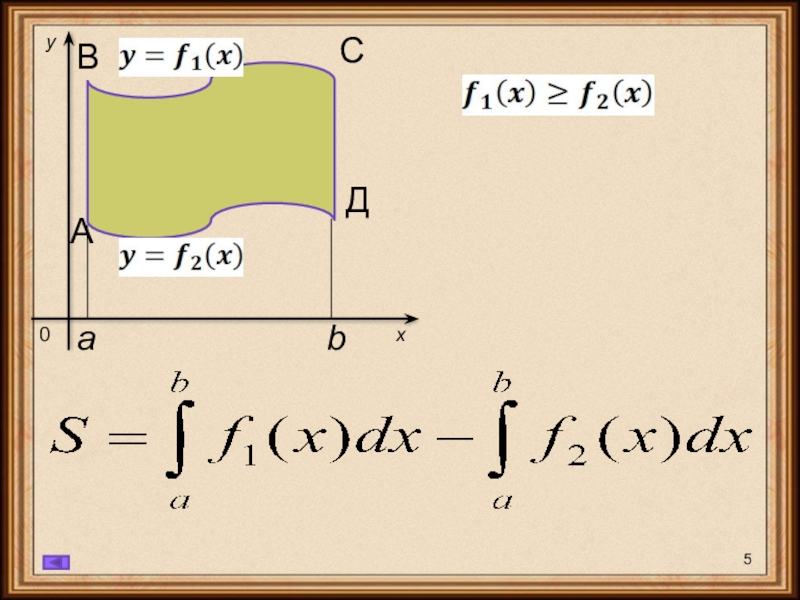
- 5. BACДху0аb
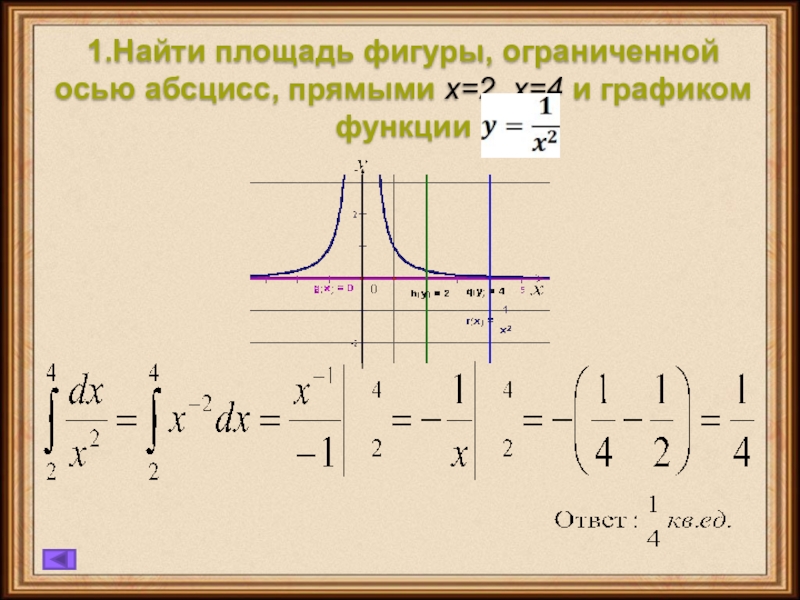
- 6. 1.Найти площадь фигуры, ограниченной осью абсцисс, прямыми х=2, х=4 и графиком функции
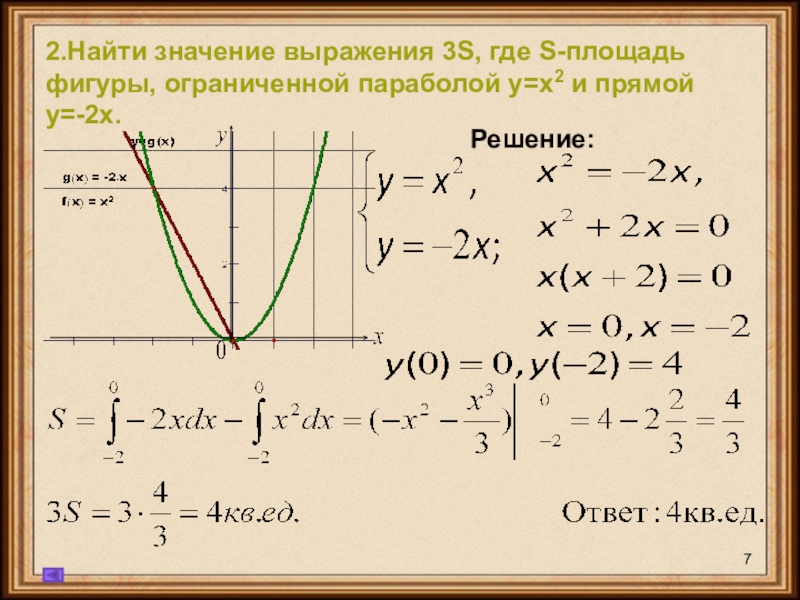
- 7. Решение:2.Найти значение выражения 3S, где S-площадь фигуры, ограниченной параболой у=х2 и прямой у=-2х.
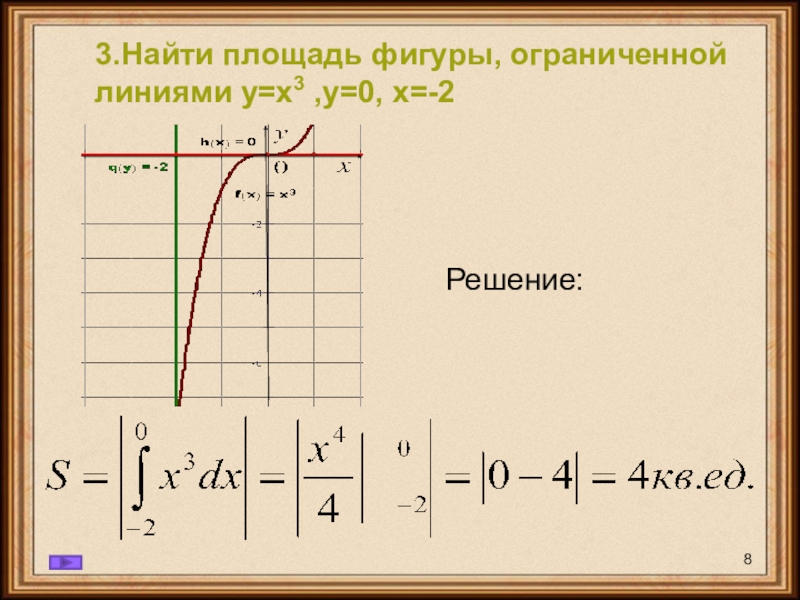
- 8. Решение:3.Найти площадь фигуры, ограниченной линиями у=х3 ,у=0, х=-2
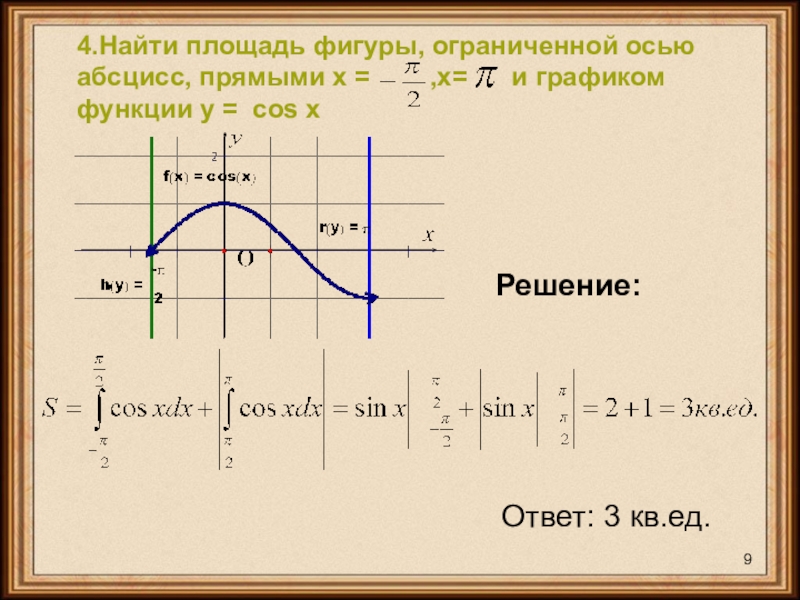
- 9. Решение:Ответ: 3 кв.ед.4.Найти площадь фигуры, ограниченной осью
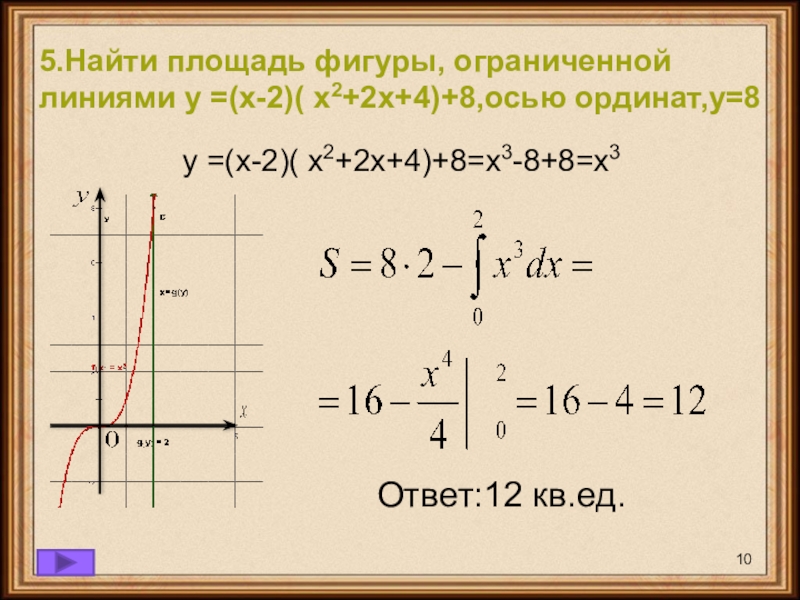
- 10. у =(х-2)( х2+2х+4)+8=х3-8+8=х3Ответ:12 кв.ед.5.Найти площадь фигуры, ограниченной линиями у =(х-2)( х2+2х+4)+8,осью ординат,у=8
- 11. Решение:Ответ: 4,5 кв.ед.6.Найти площадь фигуры, ограниченной линиями
- 12. Решение:или7.Найти площадь фигуры, ограниченной линиями у2=х2,х=0,х=3.
- 13. Домашнее задание:1.Подготовиться к контрольной работе по теме: Интегралы.2.Вычислить площадь фигуры, ограниченной линиями
- 14. Ответы к тесту
- 15. Литература:Дадаян А.А. Математика: Учебник. - М.: ФОРУМ:
Пусть функция f(x)непрерывна и неотрицательна на отрезке [a;b]. Площадь криволинейной трапеции.S
Слайд 2Пусть функция f(x)непрерывна и неотрицательна на отрезке [a;b].
Площадь криволинейной трапеции.
S
![Пусть функция f(x)непрерывна и неотрицательна на отрезке [a;b]. Площадь криволинейной трапеции.S](/img/tmb/5/477089/a1f4f9c19311d2a768cf32c9f5998394-800x.jpg "Презентация Вычисление площадей плоских фигур Пусть функция f(x)непрерывна и неотрицательна на отрезке [a;b]. Площадь криволинейной трапеции.S")
Слайд 7Решение:
2.Найти значение выражения 3S, где S-площадь фигуры, ограниченной параболой у=х2 и
прямой
у=-2х.
у=-2х.
Слайд 9Решение:
Ответ: 3 кв.ед.
4.Найти площадь фигуры, ограниченной осью абсцисс, прямыми х =
,х= и графиком функции у = cos x
Слайд 10у =(х-2)( х2+2х+4)+8=х3-8+8=х3
Ответ:12 кв.ед.
5.Найти площадь фигуры, ограниченной линиями у =(х-2)( х2+2х+4)+8,осью
ординат,у=8
Слайд 13 Домашнее задание:
1.Подготовиться к контрольной работе по теме: Интегралы.
2.Вычислить площадь фигуры,
ограниченной линиями
Слайд 15Литература:
Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2004.
Крамор В.С.Повторяем и
систематизируем школьный курс алгебры и начала анализа.-М.,Просвещение,1990
Мордкович А.Г. Алгебра и начала анализа.-М.,МНЕМОЗИНА,2007.
Мордкович А.Г. Алгебра и начала анализа.-М.,МНЕМОЗИНА,2007.
