- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Вычисление определённого интеграла
Содержание
- 1. Презентация Вычисление определённого интеграла
- 2. Цели занятия:
- 3. Этапы занятия: 1. Актуализация опорных
- 4. Актуализация опорных знаний первообразная; неопределённый интеграл; определённый интеграл; криволинейная трапеция.
- 5. Актуализация опорных знанийЕсли для любого х из
- 6. Актуализация опорных знанийСовокупность всех первообразных функций
- 7. Актуализация опорных знанийОпределённым интегралом функции f(x) называется...
- 8. Актуализация опорных знанийС помощью формулы Ньютона -Лейбница
- 9. Актуализация опорных знанийЕсли функция f(x) …………на отрезке
- 10. Актуализация опорных знанийИсправить ошибки в записи вычисления интегралов:
- 11. Закрепление материалаВычислить:
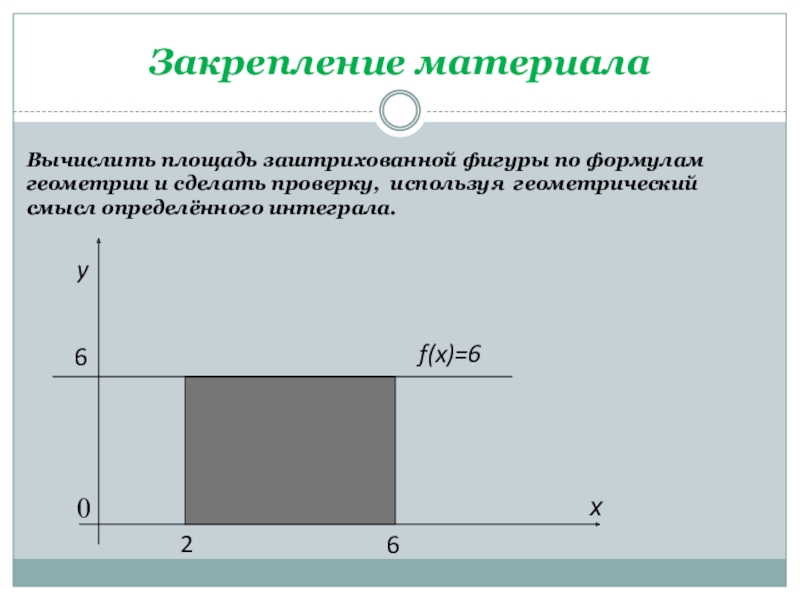
- 12. Закрепление материалаВычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку, используя геометрический смысл определённого интеграла.
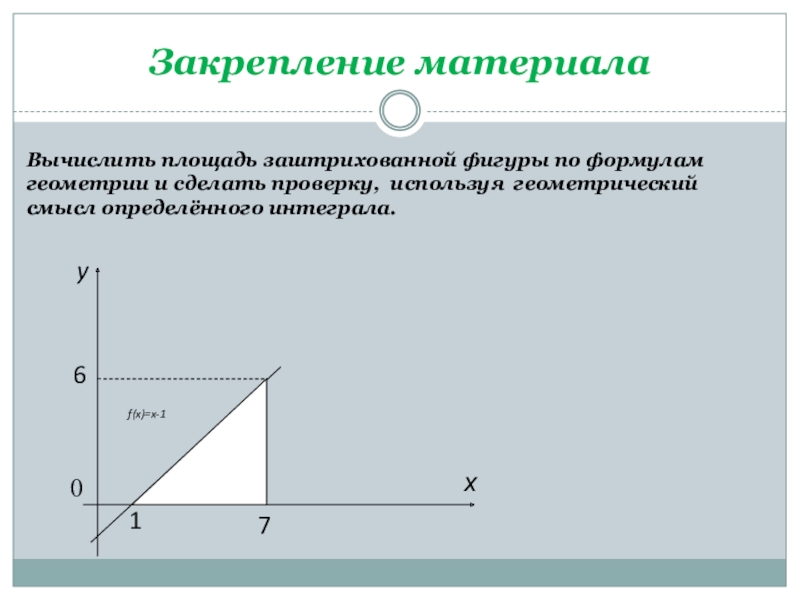
- 13. Закрепление материалаВычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку, используя геометрический смысл определённого интеграла.
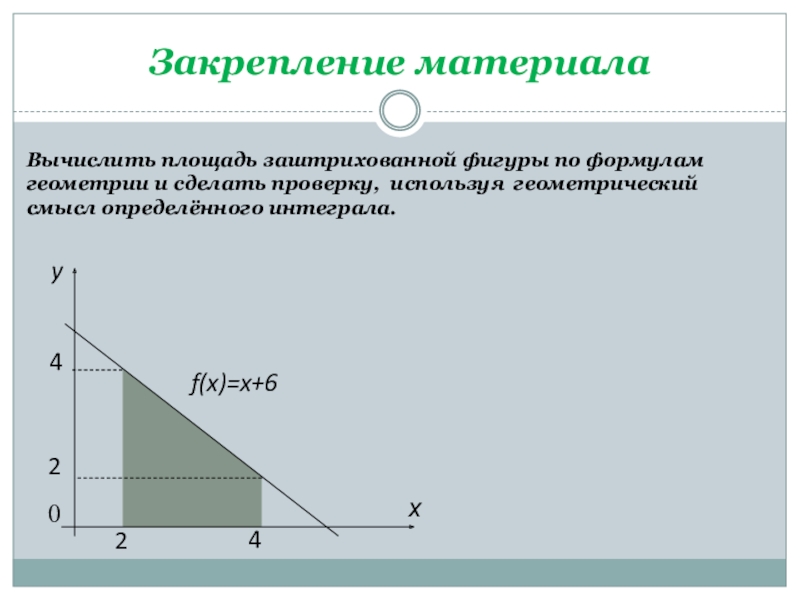
- 14. Закрепление материалаВычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку, используя геометрический смысл определённого интеграла.
- 15. Закрепление материалаВычислить определённый интеграл, используя геометрический смысл определённого интеграла.
- 16. Закрепление материалаРешение: тогда y2=16- x2 т.е.
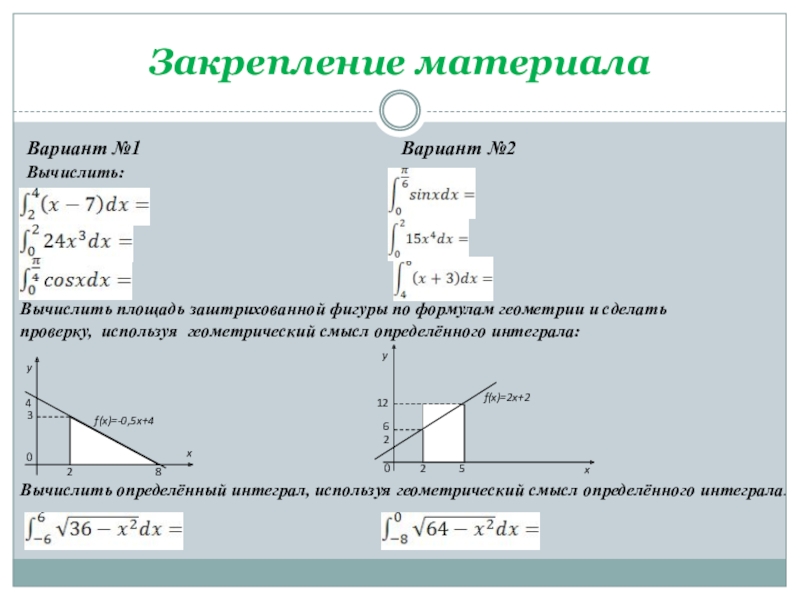
- 17. Закрепление материалаВариант №1Вариант №2Вычислить: Вычислить площадь
- 18. Домашнее задание
Цели занятия:
Слайд 3Этапы занятия:
1. Актуализация опорных знаний.
2. Закрепление материала по теме.
3. Самостоятельная работа.
4.
Домашнее задание.
Слайд 4Актуализация опорных знаний
первообразная;
неопределённый интеграл;
определённый интеграл;
криволинейная трапеция.
Слайд 5Актуализация опорных знаний
Если для любого х из множества Х выполняется равенство
F´(x) = f(x), то функцию F(x) называют … для функции f(x) на данном множестве.
А) производной;
В) первообразной;
С) обратной;
D) непрерывной.
А) производной;
В) первообразной;
С) обратной;
D) непрерывной.
Слайд 6Актуализация опорных знаний
Совокупность всех первообразных функций F(x) + С
для данной функции f(x) называется … функции f(x)
А) область определения;
В) производной;
С) область значения;
D) неопределенным интегралом.
А) область определения;
В) производной;
С) область значения;
D) неопределенным интегралом.
Слайд 7Актуализация опорных знаний
Определённым интегралом функции f(x) называется... интегральной суммы
А) преобразование;
В) предел;
С) производная;
D) остаток.
Слайд 8Актуализация опорных знаний
С помощью формулы Ньютона -Лейбница находят…
А) определенный интеграл;
В) производную;
С) обратную функцию;
D) неопределенный интеграл.
Слайд 9Актуализация опорных знаний
Если функция f(x) …………на отрезке
то справедлива формула
А)
возрастает;
В) неотрицательна;
С) имеет обратную функцию;
D) непрерывна.
В) неотрицательна;
С) имеет обратную функцию;
D) непрерывна.
,
Слайд 12Закрепление материала
Вычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку,
используя геометрический смысл определённого интеграла.
Слайд 13Закрепление материала
Вычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку,
используя геометрический смысл определённого интеграла.
Слайд 14Закрепление материала
Вычислить площадь заштрихованной фигуры по формулам геометрии и сделать проверку,
используя геометрический смысл определённого интеграла.
Слайд 15Закрепление материала
Вычислить определённый интеграл, используя геометрический смысл определённого интеграла.
Слайд 17Закрепление материала
Вариант №1
Вариант №2
Вычислить:
Вычислить площадь заштрихованной фигуры по
формулам геометрии и сделать проверку, используя геометрический смысл определённого интеграла:
Вычислить определённый интеграл, используя геометрический смысл определённого интеграла.
Слайд 18Домашнее задание
1.Башмаков М.И. Математика: учебник для начального и среднего проф. образования.– М.; «Академия», 2010.- материал стр. 196-204.
2. Башмаков М.И. Математика: задачник для начального и среднего проф. образования.– М.; «Академия», 2012.- материал стр. 277-285.
