- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл
Содержание
- 1. Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл
- 2. Проблема: найти объем мороженицы
- 3. Тема урока: Вычисление объемов тел вращения с помощью определенного интеграла
- 4. Слайд 4
- 5. Ухy=f(x)OОпределение криволинейной трапецииЕсли функция y = f(x)
- 6. Определение тела вращенияТело, полученное вращением криволинейной трапеции вокруг её основания, называется телом вращения
- 7. Ухy=f(x)OРазобьем отрезок [a;b] на n частей произвольным
- 8. Построим на каждом промежутке цилиндрическое тело, образующая
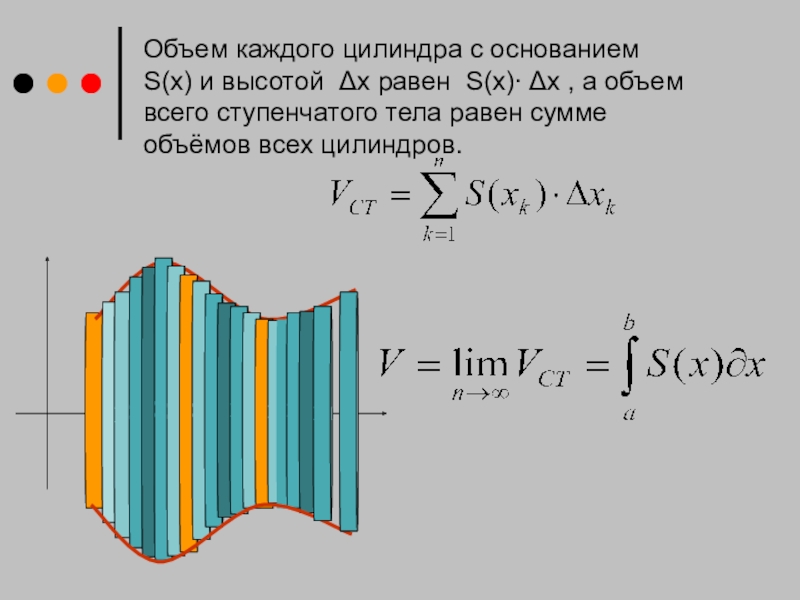
- 9. Объем каждого цилиндра с основанием S(x) и
- 10. Тогда объем тела
- 11. Замечание!Объем тела вращения вычисляется по одной из
- 12. Алгоритм решения задач:Сделать приблизительный график заданных функций,
- 13. Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ.Найдите объём тела вращения.у=х2уОх2
- 14. Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.Найдите объём тела вращения.yOx4
- 15. Теперь, давайте, рассмотрим башню для радиостанции
- 16. Задача. Пусть тело образовано вращением
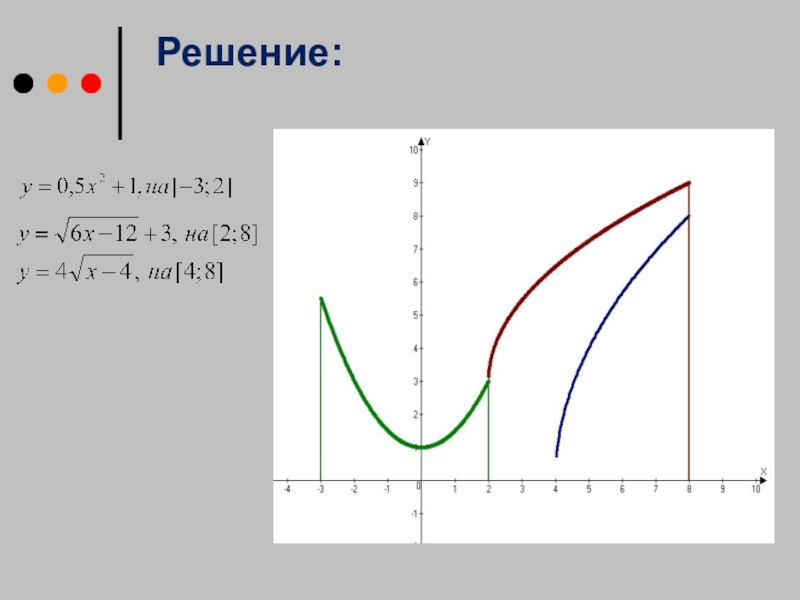
- 17. Решение проблемы: Как найти объем мороженицы?Поверхность телаполучена вращением фигуры, образованной графиками функций:
- 18. Решение:
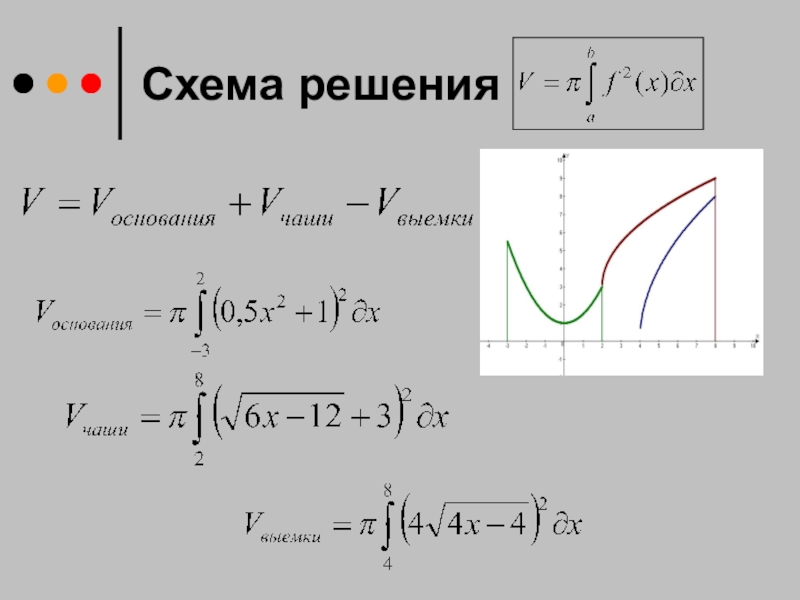
- 19. Схема решения
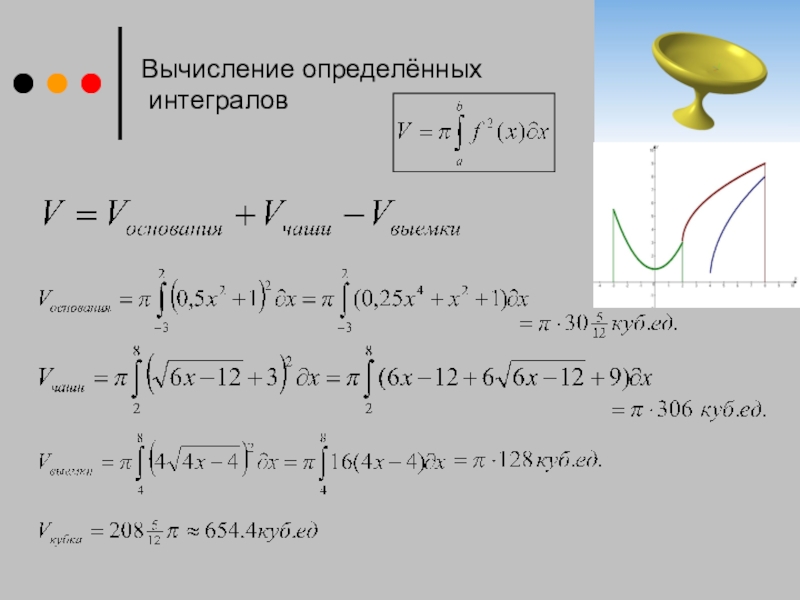
- 20. Вычисление определённых интегралов
- 21. Итог урока:Я удивился ….Я умею …Я точно знаю, что ….Я запомнил ….Я понял ….Мне было ….
- 22. Домашнее задание:п.78, выучить основные формулы;№ 674, № 675
Слайд 1УРОК №2
ВЫЧИСЛЕНИЕ ОБЪЕМОВ
ТЕЛ
Составила учитель математики
МБОУ «Красногвардейская школа №1»
Коваленко И.Н.
Слайд 4
Если функция f(x) непрерывна на промежутке числовой оси, содержащей точки х=а и х=b, то разность значений F(b)-F(a) (где F(x) - первообразная f(x) на данном промежутке называется определенным интегралом от функции f(x) от a до b.
Слайд 5У
х
y=f(x)
O
Определение криволинейной трапеции
Если функция y = f(x) определена, неотрицательна и непрерывна
Рассмотрим тело, образованное вращением этой криволинейной трапеции вокруг оси OX и найдем его объем.
a
b
Алгебра
Слайд 6Определение тела вращения
Тело, полученное вращением криволинейной трапеции вокруг её основания, называется
Слайд 7У
х
y=f(x)
O
Разобьем отрезок [a;b] на n частей произвольным образом, через каждую точку
Любое поперечное сечение тела вращения – круг.
Слайд 8
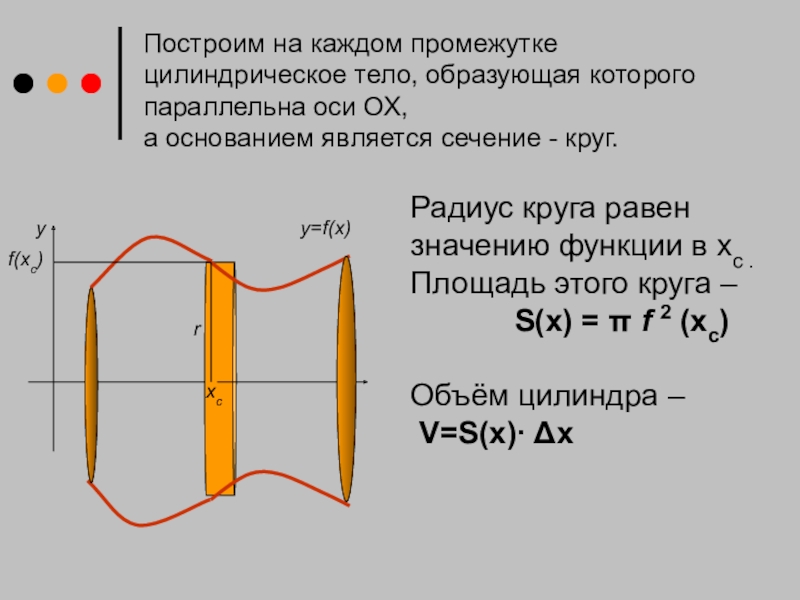
Построим на каждом промежутке цилиндрическое тело, образующая которого параллельна оси ОХ,
а
Радиус круга равен значению функции в хс .
Площадь этого круга –
S(x) = π f 2 (xс)
Объём цилиндра –
V=S(x)∙ Δx
y=f(x)
f(xс)
y
xс
r
Слайд 9
Объем каждого цилиндра с основанием S(x) и высотой Δx равен S(x)∙
Слайд 10 Тогда объем тела вращения вокруг оси ОХ:
Если
Предел полученной интегральной суммы, при n → ∞ равен определенному интегралу.
x
y=f(x)
y
Слайд 11Замечание!
Объем тела вращения вычисляется по одной из формул:
,если вращение криволинейной трапеции вокруг оси ОХ.
, если вращение криволинейной трапеции вокруг оси ОУ.
Слайд 12Алгоритм решения задач:
Сделать приблизительный график заданных функций, ограничивающих плоскую фигуру, при
Найти пределы интегрирования;
Выяснить какой формулой удобно пользоваться в данном случае;
Вычислить объем тела вращения.
Слайд 13Задача.
Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг
Найдите объём тела вращения.
у=х2
у
О
х
2
Слайд 14Задача.
Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг
Найдите объём тела вращения.
y
O
x
4
Слайд 15 Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной




![Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл Ухy=f(x)OОпределение криволинейной трапецииЕсли функция y = f(x) определена, неотрицательна и непрерывна Ухy=f(x)OОпределение криволинейной трапецииЕсли функция y = f(x) определена, неотрицательна и непрерывна на отрезке [a; b],тогда график кривой](/img/thumbs/247bb7f8b79079136d02993062a92133-800x.jpg)

![Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл Ухy=f(x)OРазобьем отрезок [a;b] на n частей произвольным образом, через каждую точку Ухy=f(x)OРазобьем отрезок [a;b] на n частей произвольным образом, через каждую точку деления проведем плоскость, перпендикулярную к оси](/img/thumbs/6d08375455849ebb4f189d09c5923f7b-800x.jpg)



![Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ.Найдите объём тела вращения.у=х2уОх2 Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ.Найдите объём тела вращения.у=х2уОх2](/img/thumbs/304cf0dcb7a74a4107a4e0a39b0a4cea-800x.jpg)
![Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.Найдите объём тела вращения.yOx4 Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.Найдите объём тела вращения.yOx4](/img/thumbs/1747787480f0474b3cc408a87d9a2616-800x.jpg)

![Презентация по геометрии в 11 классе по теме:Вычисление объемов тел вращения через интеграл Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;4] Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;4] вокруг оси ОУ. Найдите объём](/img/thumbs/1476ca491ab54dd11dc921f65833b485-800x.jpg)