- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Введение понятия комплексные числа
Содержание
- 1. Презентация Введение понятия комплексные числа
- 2. Алгебра и начала математического анализа. 11 класс.
- 3. 1Решение многих задач математики, физики и практики
- 4. Целые и дробные числа образуют множество рациональных
- 5. 2Автор предлагает рассмотреть «плюсы» и «минусы» основных
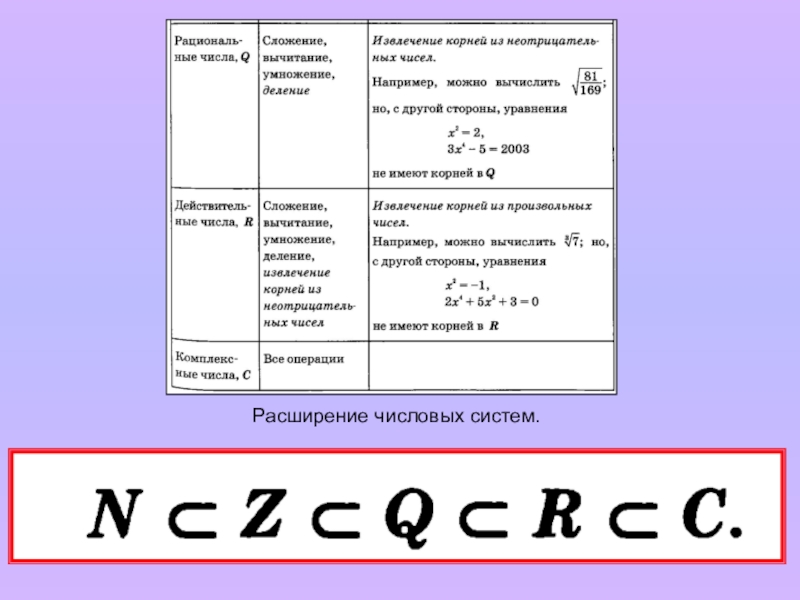
- 6. Расширение числовых систем.
- 7. Определение:Комплексным числом называют сумму действительного числа и
- 8. 3Автор учебника при введении понятия «комплексные числа»
- 9. 4Автор достаточно скупо обговаривает причину введения новых
- 10. 5«До сих пор мы рассматривали лишь действительные
- 11. «Ряд вопросов возникших при решении уравнений третьей
Слайд 2
Алгебра и начала математического анализа. 11 класс. Ю.М. Колягин;
Математика. Алгебра. Начала
Алгебра и начала математического анализа. 10 класс. А.Г. Мордкович
Алгебра и начала математического анализа. 11 класс. М.Я. Пратусевич
Алгебра и начала математического анализа. 11 класс. С.М. Никольский
1
2
3
4
5
Алгебра и начала математического анализа. 11 класс. Н.Я. Виленкин
Слайд 3
1
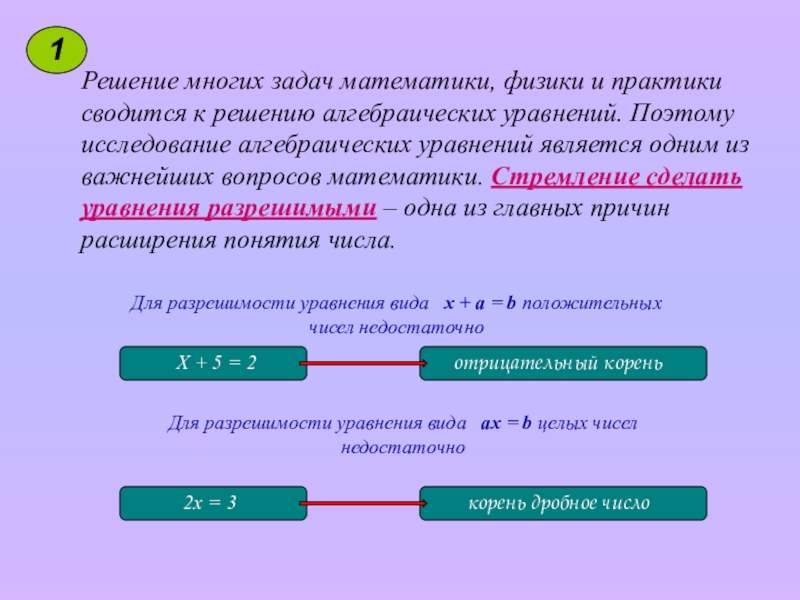
Решение многих задач математики, физики и практики сводится к решению алгебраических
Для разрешимости уравнения вида х + а = b положительных чисел недостаточно
Х + 5 = 2
Для разрешимости уравнения вида ах = b целых чисел недостаточно
2х = 3
отрицательный корень
корень дробное число
Слайд 4
Целые и дробные числа образуют множество рациональных чисел. На нем разрешимы
х 2 = 2, х3 = 5
иррациональный корень
Рациональные и иррациональные числа образуют множество действительных чисел. Но и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение.
х 2 + 1 = 0
i – комплексное число (корень уравнения)
Определение:
Комплексными числами называют выражения вида а + bi, где а и b – действительные числа, а i – некоторый символ такой, что i2 = - 1. (Ю.М. Колягин)
Комплексными числами называют упорядоченные пары (a, b) действительных чисел а и b, для которых следующим образом определены понятие равенства и опреации сложения и умножения. (М. И. Шабунин)
Слайд 5
2
Автор предлагает рассмотреть «плюсы» и «минусы» основных числовых систем. Каждая из
Слайд 7Определение:
Комплексным числом называют сумму действительного числа и чисто мнимого числа.
В записи
Слайд 8
3
Автор учебника при введении понятия «комплексные числа» опирается на исторические факты.
Учащимся
Определение:
Множеством комплексных чисел называется множество упорядоченных пар вещественных чисел (а; b) с введенными на нем двумя операциями сложения ( знак операции обозначается +) и умножения (знак операции обозначается · или ×), определенными следующим образом:
Слайд 9
4
Автор достаточно скупо обговаривает причину введения новых чисел. Появление комплексных чисел
Введение нового материала можно построить на базе материала предложенного Ю.М. Колягиным и М.И. Шабуниным.
Слайд 10
5
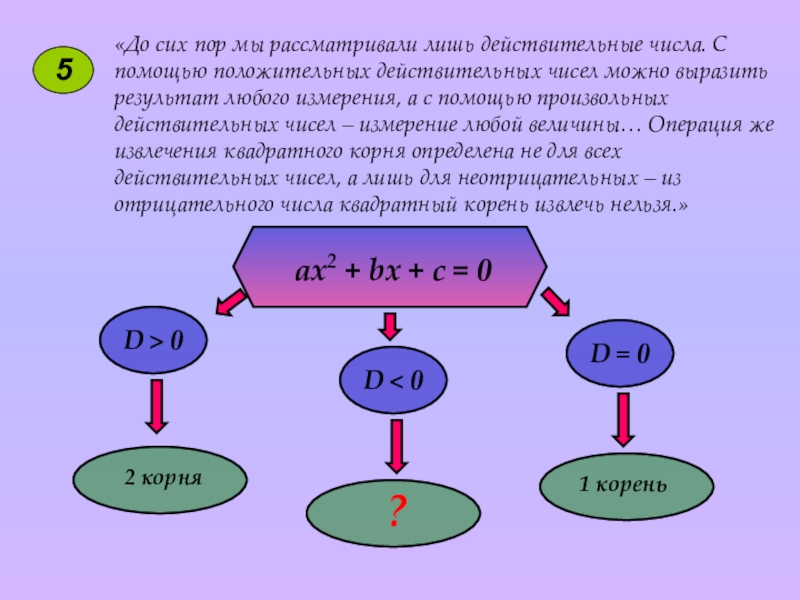
«До сих пор мы рассматривали лишь действительные числа. С помощью положительных
ax2 + bx + c = 0
D > 0
D = 0
D < 0
2 корня
1 корень
?
Слайд 11«Ряд вопросов возникших при решении уравнений третьей и четвертой степеней, привел
Определение:
Комплексным числом z называют пару (а;b) действительных чисел а и b, взятых в определенном порядке. Две пары (а;b) и (с;d) задают одно и то же комплексное число в том и только том случае, когда они совпадают, т.е. когда а = с и b = d.