- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по теме Модуль действительного числа. Уравнения и неравенства , содержащие неизвестное под знаком модуля.
Содержание
- 1. Презентация урока по теме Модуль действительного числа. Уравнения и неравенства , содержащие неизвестное под знаком модуля.
- 2. Что мы должны научиться делать?1.Использовать свойства модуля.2.Решать
- 3. Модуль действительного числа и его свойства
- 4. Свойства:│а│= │- а│.Если │а│≤ в, то -
- 5. Решение уравнений стандартными способамиРешение с использованием определения:│х
- 6. Пример: │2х - 3│= │2х +
- 7. Слайд 7
- 8. │х│ - 2 │х + 1│+ 3
- 9. 3. -1 < х
- 10. Решение уравнений нестандартными способамиЕсли │f(х)│= f(х), то
- 11. - 2х + 3 =
- 12. 2. Если │f(х)│< а,
- 13. Примеры:1). │х3 + х - 1│> х3
- 14. б) 1 ≤ х
Слайд 1Модуль действительного числа.
Уравнения и неравенства, содержащие неизвестное под знаком модуля.
Цель урока:
Слайд 2Что мы должны научиться делать?
1.Использовать свойства модуля.
2.Решать уравнения и неравенства стандартными
3.Решать уравнения и неравенства нестандартными способами.
Слайд 3Модуль действительного числа и его свойства
Модулем положительного
Модуль числа а обозначается │а│.
а, если а > 0
│а│ = -а, если а < 0
0, если а = 0.
Геометрический смысл модуля: это расстояние от начала координат до точки, которая изображает данное число на координатной прямой.
в а
--------•----------•-------•---------> х
В О А
Теорема: Модуль разности двух чисел равен расстоянию между точками, которые являются изображениями этих чисел на координатной прямой.
т.е. по рисунку АВ =│а – в │.
Пример: найти
а) │2 - √3│= 2 - √3, т.к. 2 > √3
б) │√3 - 2│= -(√3 - 2) = 2 - √3, т.к. √3 < 2.
Слайд 4Свойства:
│а│= │- а│.
Если │а│≤ в, то - в ≤ а ≤
Если │а│≥ в, то или а ≥ в, или а ≤ - в.
Модуль произведения конечного числа множителей равен произведению модулей этих множителей: │ав│ = │а│∙ │в│.
Квадрат модуля числа равен квадрату числа: │а│2 = а2.
Модуль частного равен частному от деления модуля делимого на модуль делителя:
│а/в│ = │а│ / │в│, если в ≠ 0.
Модуль суммы конечного числа действительных чисел, не превышает суммы модулей : │а + в│≤ │а│+│в│.
Модуль разности конечного числа действительных чисел не меньше модулей уменьшаемого и вычитаемого: │а - в│≥│а│-│в│.
А так же
│а + в│≥│а│-│в│.
√ а2 = │а│.
Пример: √4х2 + 12х + 9 = √ (2х + 3)2 = │2х + 3│.
Слайд 5Решение уравнений стандартными способами
Решение с использованием определения:
│х + 3│= 2.
х + 3 = 2 х + 3 = -2
х = 2 – 3 х = -2 – 3
х = -1 х = -5.
Ответ: -1; -5.
Решить уравнения: а) │2х + 1│ = 3;
б) │2х - 3│ = 9.
Решение уравнения следующих видов:
│f(х)│= │g(х)│ а) возвести левую и правую части уравнения в квадрат и
решить полученное уравнение;
б) f(х)= g(х)
Решить эту совокупность.
f(х)= - g(х)
Слайд 6
Пример: │2х - 3│= │2х + 7│ Решение:
(2х – 3)2 = (2х + 7)2
4х2 – 12х + 9 = 4х2 + 28х + 49
- 12х – 28х = 49 – 9
-40х = 40
х = -1 Ответ:-1.
2. │f(х)│= g(х). Решение данного уравнения равносильно совокупности двух систем g(х) ≥ 0
f(х) = g(х).
g(х) ≥ 0
f(х) = - g(х).
Пример: │х2 – х - 8│= - х. Решение: решим совокупность следующих систем
Слайд 7 -х ≥ 0
Решим первую систему
- х ≥ 0 х ≤ 0 х ≤ 0 х ≤ 0
х2 – х – 8 = - х, х2 – 8 = 0, х2 = 8, х = ± 2√2, х = - 2√2.
Решим вторую систему
- х ≥ 0 х ≤ 0 х ≤ 0
х2 – х – 8 = х, х2 – 2х – 8 = 0, х = 4, х = - 2, х = - 2.
Ответ: - 2, -2√2.
Метод интервалов для уравнений с неизвестным под знаком модуля.
Общие положения при решении уравнений этим методом:
Область допустимых значений;
Находим корни каждой функции;
Они делят ОДЗ на интервалы знакопостоянства функций;
На каждом интервале раскрываем модуль по определению и решаем полученное уравнение;
Проверяем принадлежность полученных корней к интервалам.
Рассмотрим применение этого метода на примере.
Слайд 8│х│ - 2 │х + 1│+ 3 │х + 2│= 0.
Х = 0, Х+ 1 = 0, Х + 2 = 0
Х = -1 Х = -2. -------------------•------•-----•-------------------->Х
-2 -1 0
Х < -2. (Раскроем модуль. Возьмем например число х = -3 и подставим в уравнение. Если выражение, стоящее под знаком модуля положительно, то знак модуля не меняется, если отрицательно – знак модуля меняется на противоположный.)
-х + 2(х + 1) – 3(х + 2) = 0,
-х + 2х + 2 – 3х – 6 = 0,
-2х – 4 = 0,
-2х = 4,
х = -2. Данное число не принадлежит рассматриваемому промежутку, а значит не является корнем уравнения.
-2 ≤ х ≤ -1. (Подставим х = -1,5.)
-х + 2(х + 1) + 3(х + 2) = 0,
-х + 2х + 2 + 3х + 6 = 0,
4х + 8 = 0,
4х = -8,
х = -2. Данное число принадлежит рассматриваемому промежутку, а значит является корнем уравнения.
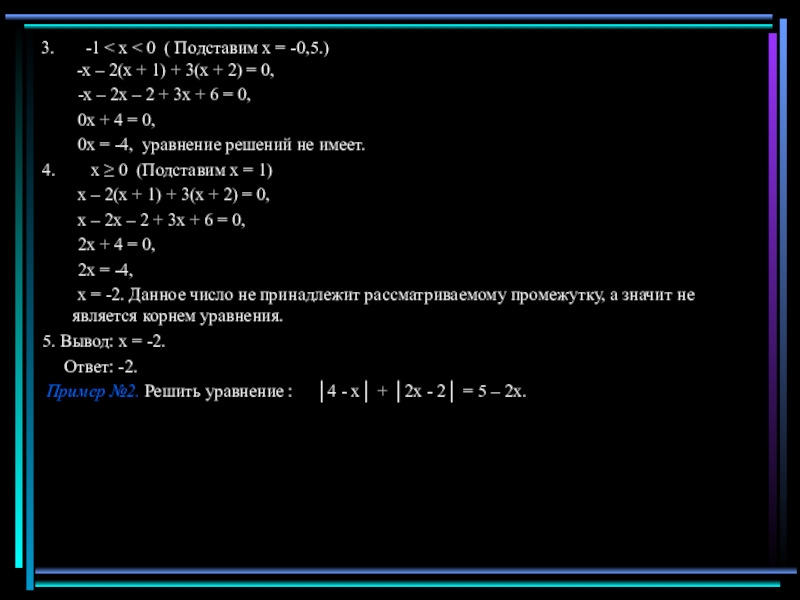
Слайд 93. -1 < х < 0 ( Подставим
-х – 2х – 2 + 3х + 6 = 0,
0х + 4 = 0,
0х = -4, уравнение решений не имеет.
4. х ≥ 0 (Подставим х = 1)
х – 2(х + 1) + 3(х + 2) = 0,
х – 2х – 2 + 3х + 6 = 0,
2х + 4 = 0,
2х = -4,
х = -2. Данное число не принадлежит рассматриваемому промежутку, а значит не является корнем уравнения.
5. Вывод: х = -2.
Ответ: -2.
Пример №2. Решить уравнение : │4 - х│ + │2х - 2│ = 5 – 2х.
Слайд 10Решение уравнений нестандартными способами
Если │f(х)│= f(х), то достаточно рассмотреть только условие
Если │f(х)│= - f(х), то рассматривается только условие f(х) ≤ 0.
Если │ f(х) │+ │g(х)│ = f(х) - g(х), то f(х) ≥ 0
g(х) ≤ 0.
Если │ f(х) │+ │g(х)│ = f(х) + g(х), то f(х) ≥ 0
g(х) ≥ 0.
Если │ f(х) │+ │g(х)│ = - f(х) + g(х), то f(х) ≤ 0
g(х) ≥ 0.
6. Если │х - а│ + │х - в│ = в – а (в > а), то а ≤ х ≤ в.
Если │х - а│ - │х - в│ = в – а (в > а), то х ≥ в.
Рассмотрим решение одного уравнения стандартным и нестандартным способами.
Пример: │х + 5│ + │х- 8│ = 13. Решение:
1. ОДЗ: хєR. х = -5, х = 8. -------•---------•------->х
-5 8
х < -5 (подставим -6) -5 ≤ х ≤ 8 (х = 0) х > 8 (х = 10)
-(х+5) – (х-8) = 13, (х+5) – (х-8) = 13, (х+5) + (х-8) = 13,
-х – 5 –х +8 = 13, х + 5 – х + 8 = 13, х + 5 + х – 8 = 13,
Слайд 11 - 2х + 3 = 13,
- 2х = 10, 0х = 0, 2х = 16,
х = - 5. х – любое число. х = 8.
число не принадлежит решением является число не принадлежит
данному промежутку, весь рассматриваемый данному промежутку,
значит не является промежуток -5 ≤ х ≤ 8 . значит не является
решением уравнения. решением уравнения
Ответ: х є [ -5 ; 8 ].
2. │х + 5│ + │х- 8│ = 13. Решение:
ОДЗ: хєR.
а = -5, в = 8, значит в – а = 8 + 5 = 13, т.о. -5 ≤ х ≤ 8.
Ответ: х є [ -5 ; 8 ].
Решить самостоятельно: │х + 3│ - │х- 2│= 5.
Решение неравенств
Рассмотрим несколько случаев решения неравенств:
Если │f(х)│> а, то а) а > 0 f(х) > а б) а ≤ 0 Решением будет ОДЗ f(х)
f(х) < -а
Слайд 12 2. Если │f(х)│< а, то а) а
3. Если │f(х)│> f(х), то f(х) < 0 ,
│f(х)│≥ f(х), то решением являются все значения из ОДЗ.
4. Если │f(х)│≤ f(х), то f(х) ≥ 0;
│f(х)│< f(х), то решения нет.
5. Если │ f(х)│> g(х), то f(х) > g(х)
f(х) < - g(х).
6. Если │f(х)│< g(х), то f(х) < g(х)
f(х) > - g(х).
7. Знак разности модулей двух выражений, совпадает со знаком разности квадратов этих выражений.
Например, в записи это будет так : │х3 + х - 1│ - │х3 – х + 1│заменим выражением
(х3 + х – 1)2 – (х3 – х + 1)2.
8. А если вы забыли все способы решения неравенств, то его можно решить, применив метод интервалов.
Слайд 13Примеры:
1). │х3 + х - 1│> х3 – х + 1
х3 + х – 1 > х3 – х + 1 2х > 2 х > 1 х > 1
х3 + х – 1 < - х3 + х – 1 , 2х3 < 0, х3 < 0, х < 0. Решением этой совокупности является
хє ( -∞; 0) U ( 1; +∞).
Ответ: ( -∞; 0) U ( 1; +∞).
2). Найти наибольшее целое решение неравенства: │х – 5│ < 4.
(Такого типа неравенства чаще всего встречаются в 1-й части тестовой тетради на ВНО)
Решим неравенство, использовав свойство №2.
- 4 < х – 5 < 4,
1 < х < 9, т.о. х є ( 1; 9) и наибольшее целое решение
х = 8.
Решение неравенства методом интервалов:
│х - 1│ + │х - 2│≥ х + 3. Решение: ОДЗ: хєR.
х = 1, х = 2 ---------------•-----------•-----------------> х
1 2
а) х < 1 //////////////////////////////
-(х – 1) – (х – 2) ≥ х + 3, ------------•----------◦------------> х
-х + 1 – х + 2 ≥ х + 3, /////////////0 1
- 3х ≥ 0,
х ≤ 0 значит хє ( -∞; 0 ].
Слайд 14 б) 1 ≤ х ≤ 2
х – 1 – х + 2 ≥ х + 3, /////////
-х ≥ 2, ------------•--------•-----•----------> х
х ≤ -2. //////////////-2 1 2
решения нет.
в) х > 2
(х – 1) + (х – 2) ≥ х + 3, //////////////////////////////////
х – 1 + х – 2 ≥ х + 3, ------------◦--------------•-------------> х
х ≥ 6. 2 6///////////////
значит хє [6; + ∞).
Т.о. хє ( -∞; 0 ] U [6; + ∞). Ответ: ( -∞; 0 ] U [6; + ∞).
Решить уравнения и неравенства.
а) │х + 1│ + │х - 2│ = 3; Домашнее задание:
б) │х - 1│ + │х - 2│ = │х - 3│ + 4; Глава 6,§ 1.
в) │х - 1│ + │х - 3│ = 2х – 4; № 2 (2,3,7), № 3 (1,8).
г) │2х - 1│ - │х - 4│ > 4;
д)│3х - 5│ > 9х + 1.