- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по алгебре в 8 классе Квадратные уравнения
Содержание
- 1. Презентация урока по алгебре в 8 классе Квадратные уравнения
- 2. Изучить теорему Виета. Закрепить тему «Квадратные уравнения».
- 3. Квадратным уравнением называется уравнение вида a x
- 4. ИсторияЗадачи на квадратные уравнения встречаются уже в
- 5. Классификация .Квадратные уравнения.неполноеполноеа х 2+ в х
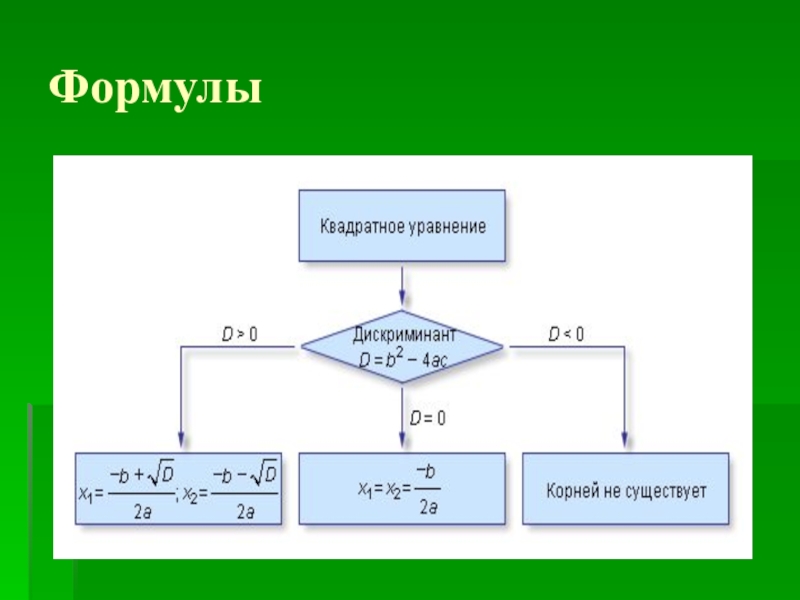
- 6. Формулы
- 7. Примеры решения квадратного уравнения по формуле2x2+4x+7=0D=b2-4aс;D=16-56=-40;D0 уравнение
- 8. Виды квадратных уравнений1) х² + 4х +3
- 9. Решить квадратное уравнение- значит найти все его
- 10. Реши квадратное уравнение по формуле 5x2- 13x +6=0 4x2- x +1=0 8x(1+2x)=-1
- 11. 1) 5x2 - 13x + 6 =0D=49;
- 12. Теорема Виета. Если х1 и х2 корни
- 13. Пример решения квадратного уравнения по теореме, обратной теореме Виетаx2-6x +8=0X1+X2=6X1X2=8Ответ: 2;4.
- 14. Для уравнения, имеющего корни х1 и х2,
- 15. Угадай!Задание 1. У какого из заданных квадратных
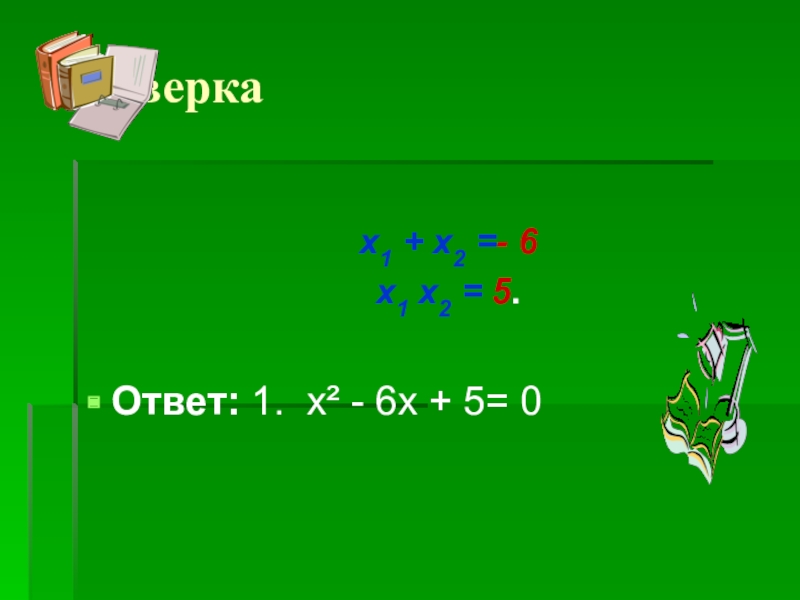
- 16. Проверка x1 + x2 =-
- 17. Подумай!Задание 2. Если х1 = -5 и
- 18. Молодец! Верный ответ:2) p = 5, q = 6
- 19. Найти подбором корни уравнения х² +
- 20. ПроверкаВ. 4 и -11;
- 21. Решите уравнение с помощью теоремы, обратной теореме Виетаx2-2x-8=0x2-7x+10=0x2-5x+6=0x2+2005x-2006=0
- 22. 1. x2 - 5x+6=0; x1+x2=5; x1x2=6Ответ:x1=2,
- 23. 3. Найдите подбором корни уравнений
- 24. Верные ответы 1. х1=3 х2=82. х1=-4 х2=-63. х1=-2 х2=7
- 25. Связь корней квадратного уравнения с коэффициентами и
- 26. Решите уравнение используя связь корней квадратного уравнения с коэффициентами и свободным членом.1) 5x2-7x+2=02) 11x2+27x+16=0
- 27. 5x2 – 7x +2=0; 5+(-7)+2=0Ответ:х1=1; х2=0,4Проверка
- 28. Оцени свою работу
- 29. Приёмы устного решения квадратных уравнений.a x 2+
- 30. Ситуации, в которых может использоваться теорема Виета.
- 31. Немного историиЕще
- 32. Франсуа ВиетФранцузский математик родился в 1540 году.
- 33. Стихотворение По праву достойна в стихах быть
- 34. Штифель (1486 – 1567) в 1544 году
- 35. Научился сам - научи другого.
Слайд 1
Квадратные уравнения.
Учитель математики МБОУ «Красноармейская СОШ»
Андреева Рена Валерьяновна
Теорема Виета
Слайд 2Изучить теорему Виета. Закрепить тему «Квадратные уравнения». Систематизировать знания, умения, навыки
Исследовать зависимость между коэффициентами и корнями квадратного уравнения.
Слайд 3Квадратным уравнением называется уравнение вида a x 2+ b x +
где х – переменная,
a, b и c – некоторые числа, причём а ≠ 0.
a x2 + b x + c = 0
Первый коэффициент
Второй коэффициент
Свободный
член
Слайд 4История
Задачи на квадратные уравнения встречаются уже в 499 г. В Древней
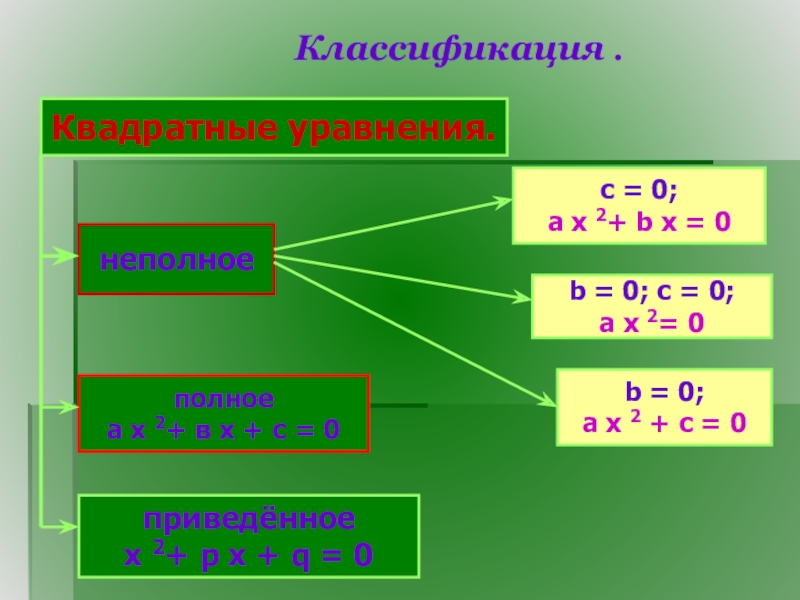
Слайд 5Классификация .
Квадратные уравнения.
неполное
полное
а х 2+ в х + с = 0
приведённое
x
c = 0;
a x 2+ b x = 0
b = 0; c = 0;
a x 2= 0
b = 0;
a x 2 + c = 0
Слайд 7Примеры решения квадратного уравнения по формуле
2x2+4x+7=0
D=b2-4aс;
D=16-56=-40;
D0 уравнение
имеет два
корня.
X1=1; X2=-11
3
Слайд 8Виды квадратных уравнений
1) х² + 4х +3 = 0
2) 2х² +
3) 7х² - 28= 0
4) х² + 5х – 1 = 0
5) х² – 13х = 0
6) 3х² - 5х + 19 = 0
Слайд 9Решить квадратное уравнение- значит найти все его корни или установить, что
Ответ:
1) -1; -3
3) -2; 2.
5) 0; 13.
Слайд 111) 5x2 - 13x + 6 =0
D=49; Ответ:x1=2 x2=0,6
2) 4x2 –x
D=-15, нет действительных корней
3) 8x(1+2x)=-1
16x2 + 8x + 1=0
D=0 Ответ: x=-0,25
Проверка
Слайд 12Теорема Виета.
Если х1 и х2 корни приведённого квадратного
уравнения
то x1 + x2 = - p, а x1 x2 = q.
Обратное утверждение:
Если числа m и n таковы, что m + n = - p, mn = q, то эти числа являются корнями уравнения х2 + px + q = 0.
Обобщённая теорема:
Числа х1 и х2 являются корнями приведённого квадратного уравнения х2 + px + q = 0 тогда и только тогда, когда x1 + x2 = - p, x1 x2 = q.
Следствие: х2 + px + q = (х – х1)(х – х2)
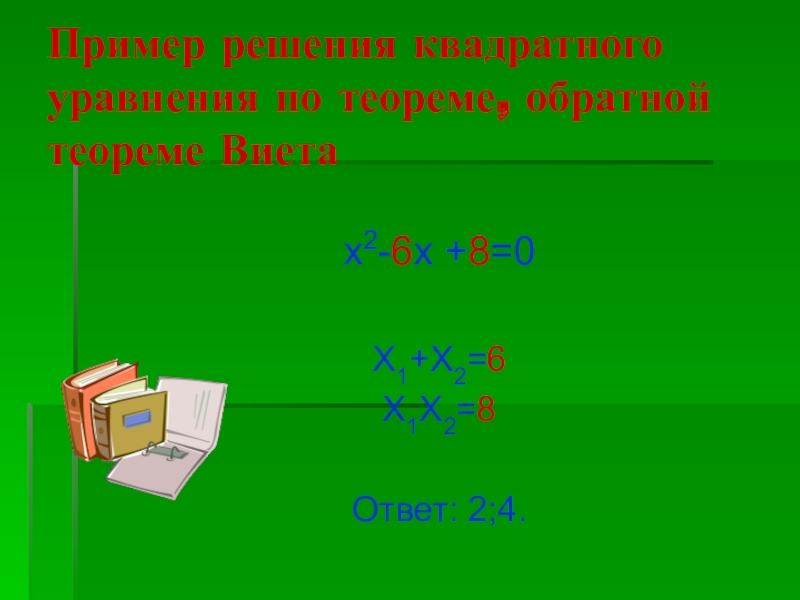
Слайд 13Пример решения квадратного уравнения по теореме, обратной теореме Виета
x2-6x +8=0
X1+X2=6
X1X2=8
Ответ: 2;4.
Слайд 14Для уравнения, имеющего корни х1 и х2, найдите их сумму и
а) х² - 7х +12 = 0,
х1 + х2 =________,
х1 ∙ х2 =______.
б) 2х² + 14х - 6 = 0,
х1 + х2 =________,
х1 ∙ х2 =_______.
Слайд 15Угадай!
Задание 1. У какого из заданных квадратных уравнений сумма корней равна
1. х² - 6х + 5= 0
2. х² + 6х - 5= 0
3. х² + 6х + 5 = 0
4. х² - 5х - 6 = 0
5. х² + 5х - 6 = 0
Слайд 17Подумай!
Задание 2. Если х1 = -5 и х2 = -1 -
1) p = -6, q = -5
2) p = 5, q = 6
3) p = 6, q = 5
Слайд 19Найти подбором корни уравнения
х² + 7х - 44 = 0.
Выберите верный ответ.
А. 4 и 11;
Б. -4 и 11;
В. 4 и -11;
Г. -4 и -11.
Слайд 21Решите уравнение с помощью теоремы, обратной теореме Виета
x2-2x-8=0
x2-7x+10=0
x2-5x+6=0
x2+2005x-2006=0
Слайд 221. x2 - 5x+6=0; x1+x2=5; x1x2=6
Ответ:x1=2, x2=3
2. x2 – 7x+10=0;
Ответ:x1=2; x2=5
3. x2+2005x-2006=0;
x1+x2=-2005; x1x2=-2006
Ответ:x1=-2006; x2=1
Проверка
Слайд 23 3. Найдите подбором корни уравнений и сделайте проверку:
а)
б) х2 + 10х + 24 = 0,
в) х2 - 5х - 14 = 0.
Слайд 25Связь корней квадратного уравнения с коэффициентами и свободным членом
Если сумма коэффициентов
a
Если
a -b + c=0,
то
Слайд 26Решите уравнение используя связь корней квадратного уравнения с коэффициентами и свободным
1) 5x2-7x+2=0
2) 11x2+27x+16=0
Слайд 29Приёмы устного решения квадратных уравнений.
a x 2+ b x + c
Основа: f (x) = a x 2+ b x + c ;
f (1) = a + b + c; f (- 1) = a - b + c.
1.Если a + b + c = 0, то один корень уравнения x = 1, а второй x = c/a.
2.Если a - b + c = 0, то один корень уравнения x = - 1, а второй x = - c/a.
Слайд 30Ситуации, в которых может
использоваться теорема Виета.
Проверка правильности найденных корней.
Устное нахождение целых корней приведённого квадратного уравнения.
Составление квадратных уравнений с заданными корнями.
Разложение квадратного трёхчлена на множители.
Слайд 31 Немного истории
Еще в древнем Вавилоне могли
Диофант Александрийский и Евклид , Аль-Хорезми и Омар Хайям решали уравнения геометрическими и графическими способами.
В 1591 году Франсуа Виет ввел формулы для решения квадратных уравнений
Слайд 32Франсуа Виет
Французский математик родился
в 1540 году. Получив юридическое образование он
Слайд 33Стихотворение
По праву достойна в стихах быть воспета
О свойствах корней теорема
Что лучше, скажи, постоянства такого:
Умножишь ты корни — и дробь уж готова?
В числителе с, в знаменателе а.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в , в знаменателе а.
Слайд 34Штифель (1486 – 1567) в 1544 году сформировал общее правило решения
x2 + bx = c
при всевозможных комбинациях знаков и коэффициентов b и c.
Франсуа Виет (1540 – 1603) вывел формулы решения квадратного уравнения в общем виде, однако он признавал только положительные числа.
Итальянские учёные Тарталья, Кардано, Бомбелли среди первых в XVI веке учитывают, помимо положительных, и отрицательные корни.
В XVII веке благодаря трудам Жиррара, Декарта, Ньютона и других учёных, способ решения квадратных уравнений принимает современный вид.