Подготовила: Преподаватель математики ГАПОУ Белорецкий Строительный колледж г. Белорецк
Лапшина Любовь Николаевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад .Урок Смотр знаний по математике по теме Квадратичная функция, её свойства и график
Содержание
- 1. Презентация .Урок Смотр знаний по математике по теме Квадратичная функция, её свойства и график
- 2. Цели урокаОбразовательная цель: Обобщить и систематизировать
- 3. Рефлексия«Моё состояние»Нарисуйте изображение человечка на соответствующую ступеньку
- 4. Скажи мне - и я забуду,
- 5. План урокаI .Организационный момент.
- 6. Математический диктант1.Квадратичной функцией называется функция, которую можно
- 7. 1.2.3.4.5.Указать формулу, которой задается квадратичная функция
- 8. Свойства функцииа > 0
- 9. у =
- 10. Какую информацию можно получить о графике квадратичной
- 11. Определите знаки коэффициентов a, са) а >
- 12. Построение графика у =ах2 + n
- 13. а) у = б) у =х
- 14. Построение графика y =a (x –
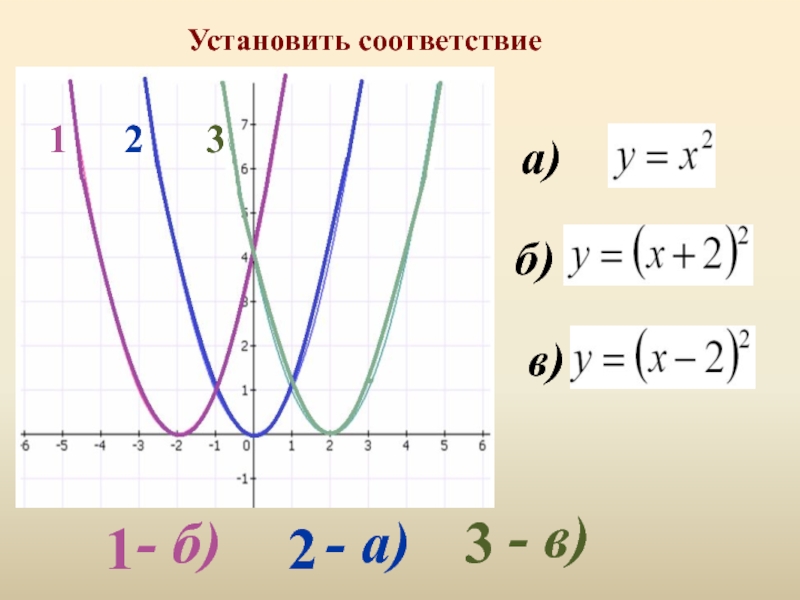
- 15. а)б)в)113232- б)- в)- а)Установить соответствие
- 16. Построение графика y =a (x –
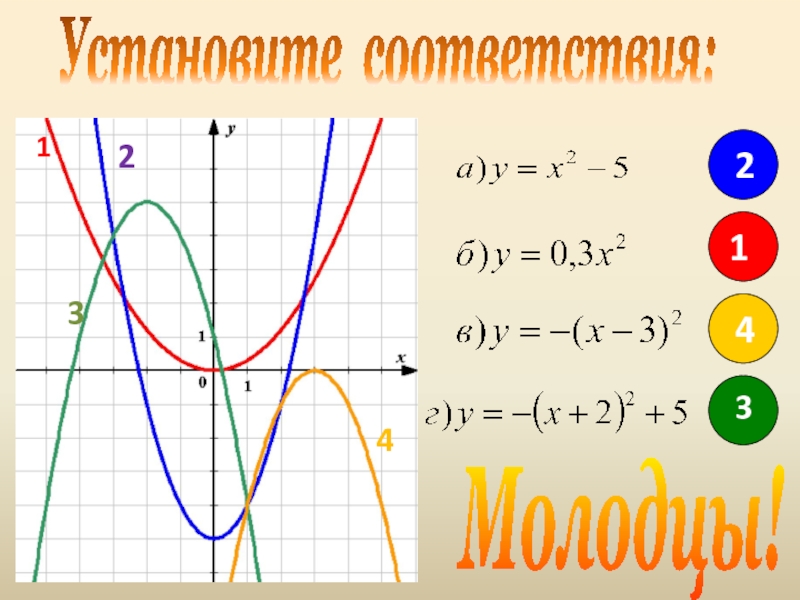
- 17. Установите соответствия:Молодцы!23431412
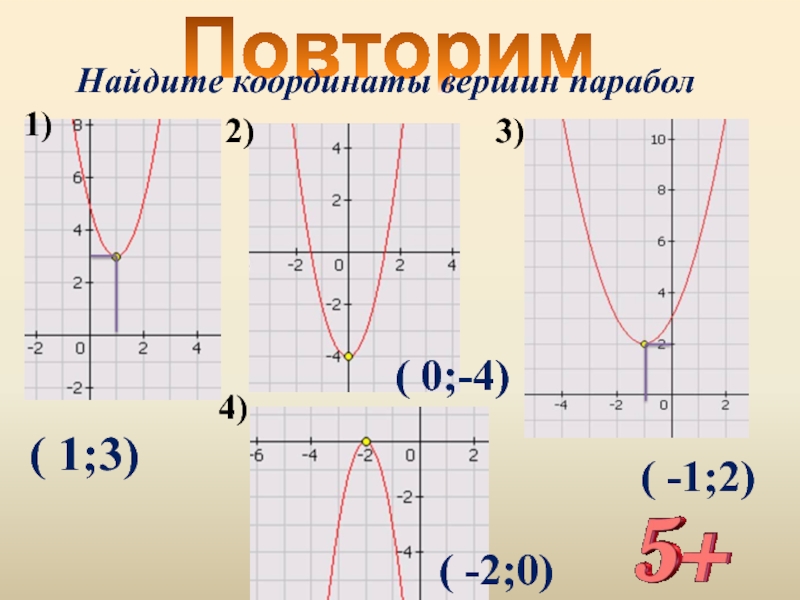
- 18. Повторим Найдите координаты вершин парабол1)4)3)2)( 1;3)( 0;-4)( -1;2)( -2;0)
- 19. Используя шаблоны
- 20. Ответы: I ряд
- 21. Сообщение из истории развития функции В математике
- 22. Если вращать параболу вокруг оси ее симметрии, то получается интересная поверхность, которая называется параболоидом вращения.
- 23. Связь с реальным миром
- 24. Слайд 24
- 25. В согласии с природой
- 26. Слайд 26
- 27. Слайд 27
- 28. Парабола- явление в природеЛуч светаРадуга
- 29. Параболические траектории струй воды
- 30. У прожекторов зеркало обычно делается в форме
- 31. АнтеннаСолнечные печи, нагреватели.
- 32. Падение баскетбольного мяча
- 33. Оценка: «
- 34. Слайд 34
- 35. Спасибо за внимание
Цели урокаОбразовательная цель: Обобщить и систематизировать знания учащихся по теме «Квадратичная функция, ее свойства и график». Развивающая цель: Развитие умения логически обосновывать суждения, использовать различные языки математики (словесный, символический, графический). Способствовать развитию самостоятельности, чувства
Слайд 1Квадратичная функция, ее свойства и график.
Алгебра 9 класс.
Урок
« смотр знаний.»
Слайд 2Цели урока
Образовательная цель: Обобщить и систематизировать знания учащихся по теме
«Квадратичная функция, ее свойства и график».
Развивающая цель: Развитие умения логически обосновывать суждения, использовать различные языки математики (словесный, символический, графический). Способствовать развитию самостоятельности, чувства ответственности, правильной самооценки.
Воспитательная цель: Воспитание интереса к предмету, к изучаемому учебному материалу
Развивающая цель: Развитие умения логически обосновывать суждения, использовать различные языки математики (словесный, символический, графический). Способствовать развитию самостоятельности, чувства ответственности, правильной самооценки.
Воспитательная цель: Воспитание интереса к предмету, к изучаемому учебному материалу
Слайд 3Рефлексия
«Моё состояние»
Нарисуйте изображение человечка
на соответствующую ступеньку лесенки
______Комфортно
Уверен в своих силах
Хорошо
Плохо
Крайне скверно
Уверен в своих силах
Хорошо
Плохо
Крайне скверно
Слайд 4 Скажи мне - и я забуду, Покажи мне - и я запомню, Вовлеки
меня – и я пойму
Древняя китайская мудрость
Эпиграф:
Слайд 5План урока
I .Организационный момент.
Рефлексия «Моё состояние»
II. .Актуализация опорных знаний
а) Математический диктант
б) Установить соответствие
в) Устная работа
III. Практическая часть
а). Устная работа (построение графиков)
б) Самостоятельная работа
IV. Сообщение по истории развития понятия функции
V . Итог
VI. Рефлексия (Анкета самоанализа )
Слайд 6Математический диктант
1.Квадратичной функцией называется функция, которую можно задать формулой . .
.
где а,b,с - некоторые числа, причём а не равно нулю.
2. Графиком квадратичной функцией является . . .
3. Расположение графика зависит от . . . .
4. Если коэффициент а > 0. то . . . .
5. Если коэффициент а < 0. то . . . .
где а,b,с - некоторые числа, причём а не равно нулю.
2. Графиком квадратичной функцией является . . .
3. Расположение графика зависит от . . . .
4. Если коэффициент а > 0. то . . . .
5. Если коэффициент а < 0. то . . . .
у = ах2 + bх + с
парабола
коэффициента а
ветви направлены вверх
ветви направлены вниз
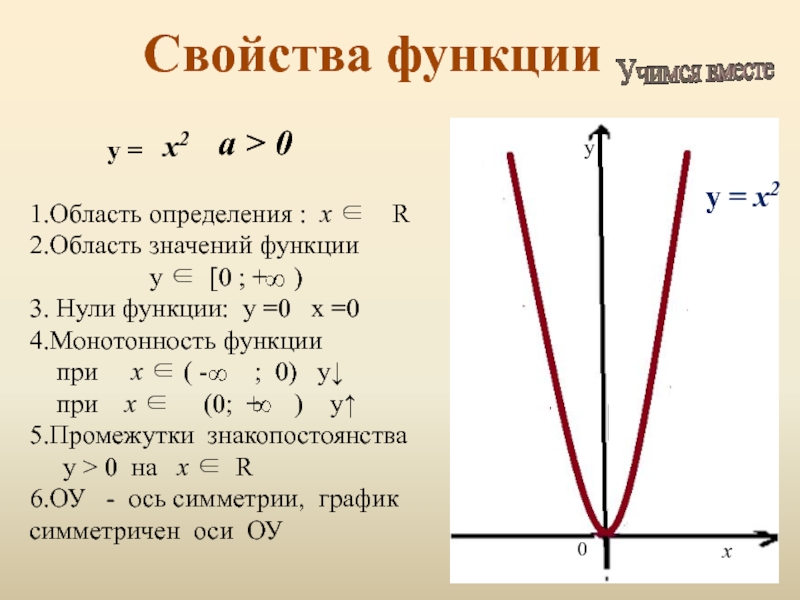
Слайд 8Свойства функции
а > 0
у =
1.Область определения : х ∈ R
2.Область значений функции
у ∈ [0 ; + )
3. Нули функции: у =0 х =0
4.Монотонность функции
при х ∈ ( - ; 0) у↓
при х ∈ (0; + ) у↑
5.Промежутки знакопостоянства
y > 0 на х ∈ R
6.ОУ - ось симметрии, график симметричен оси ОУ
1.Область определения : х ∈ R
2.Область значений функции
у ∈ [0 ; + )
3. Нули функции: у =0 х =0
4.Монотонность функции
при х ∈ ( - ; 0) у↓
при х ∈ (0; + ) у↑
5.Промежутки знакопостоянства
y > 0 на х ∈ R
6.ОУ - ось симметрии, график симметричен оси ОУ
x2
у = х2
у
х
0
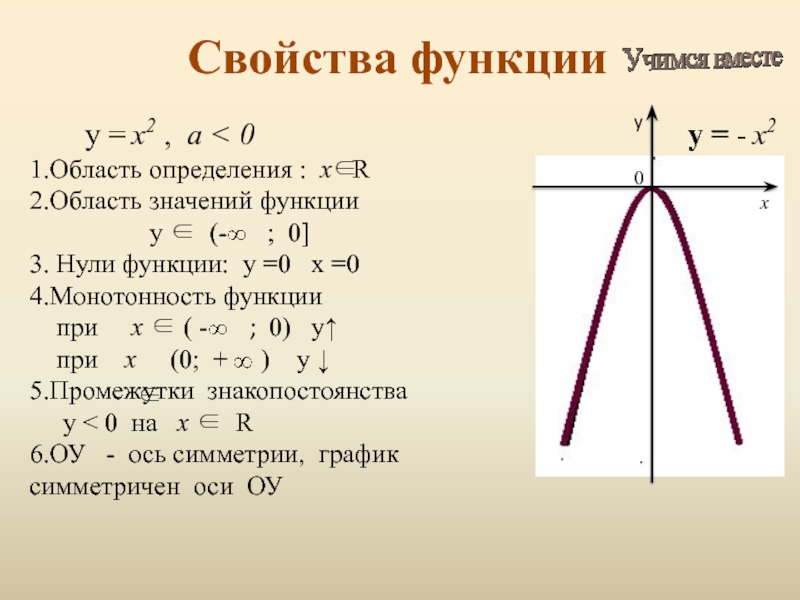
Слайд 9 у =
1.Область определения : х
R
2.Область значений функции
у ∈ (- ; 0]
3. Нули функции: у =0 х =0
4.Монотонность функции
при х ∈ ( - ; 0) у↑
при х (0; + ) у ↓
5.Промежутки знакопостоянства
y < 0 на х ∈ R
6.ОУ - ось симметрии, график симметричен оси ОУ
2.Область значений функции
у ∈ (- ; 0]
3. Нули функции: у =0 х =0
4.Монотонность функции
при х ∈ ( - ; 0) у↑
при х (0; + ) у ↓
5.Промежутки знакопостоянства
y < 0 на х ∈ R
6.ОУ - ось симметрии, график симметричен оси ОУ
Свойства функции
x2 , а < 0
y
x
∈
∈
x2
у = -
0
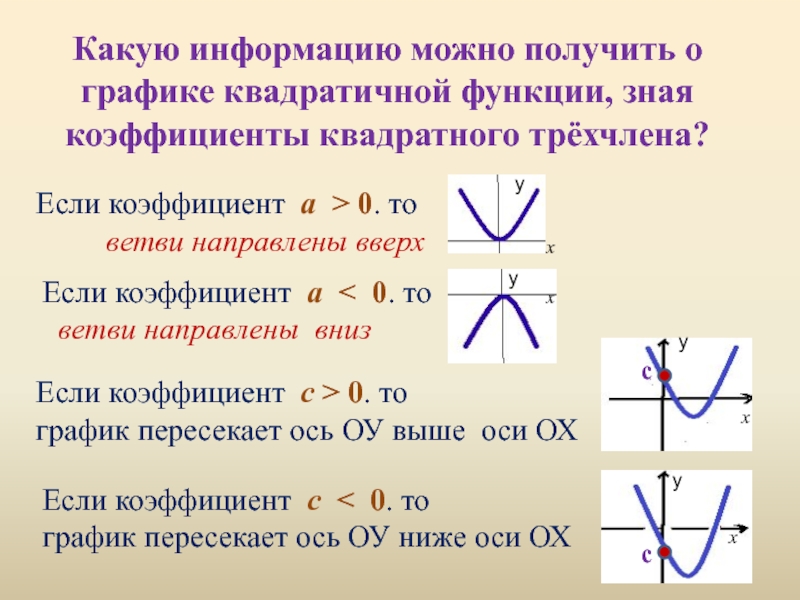
Слайд 10Какую информацию можно получить о графике квадратичной функции, зная коэффициенты квадратного
трёхчлена?
Если коэффициент а > 0. то
ветви направлены вверх
Если коэффициент а < 0. то
ветви направлены вниз
у
х
у
х
Если коэффициент с > 0. то
график пересекает ось ОУ выше оси ОХ
Если коэффициент с < 0. то
график пересекает ось ОУ ниже оси ОХ
х
у
с
х
у
с
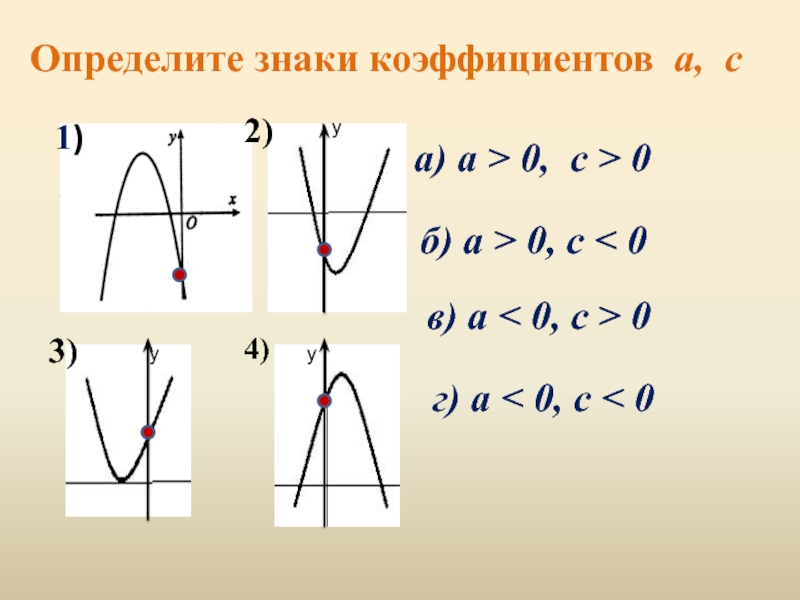
Слайд 11Определите знаки коэффициентов a, с
а) а > 0, с > 0
1)
б) а > 0, с < 0
г) а < 0, с < 0
в) а < 0, с > 0
2)
у
у
3)
у
4)
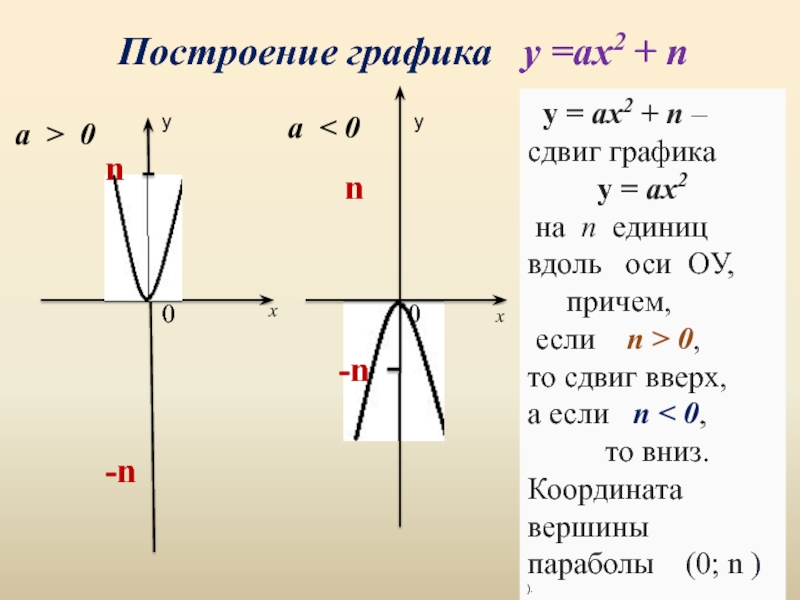
Слайд 12Построение графика у =ах2 + n
у
х
у
х
a > 0
a
< 0
n
-n
n
-n
y = аx2 + n –
сдвиг графика
y = аx2
на n единиц вдоль оси OУ,
причем,
если n > 0,
то сдвиг вверх,
а если n < 0,
то вниз.
Координата вершины параболы (0; n )
).
0
0
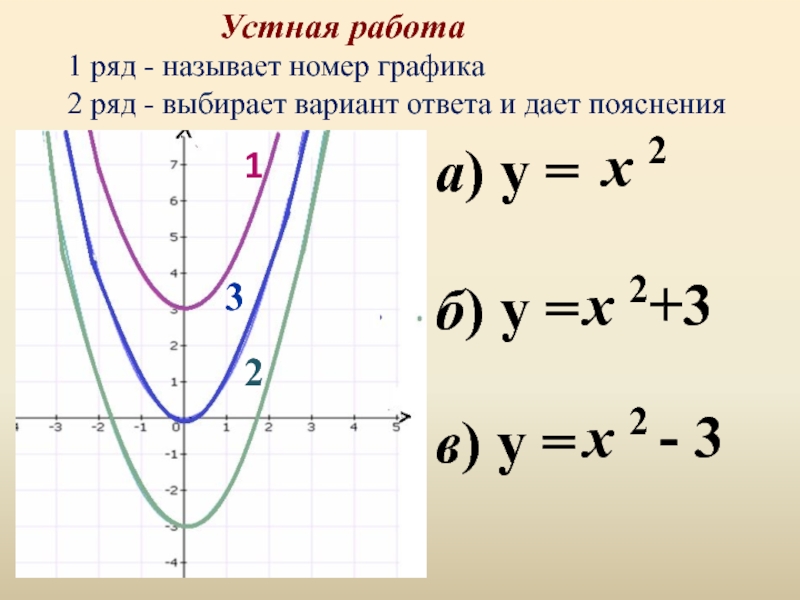
Слайд 13 а) у =
б) у =
х 2
в) у =
1
2
х
2+3
х 2 - 3
Устная работа
1 ряд - называет номер графика
2 ряд - выбирает вариант ответа и дает пояснения
3
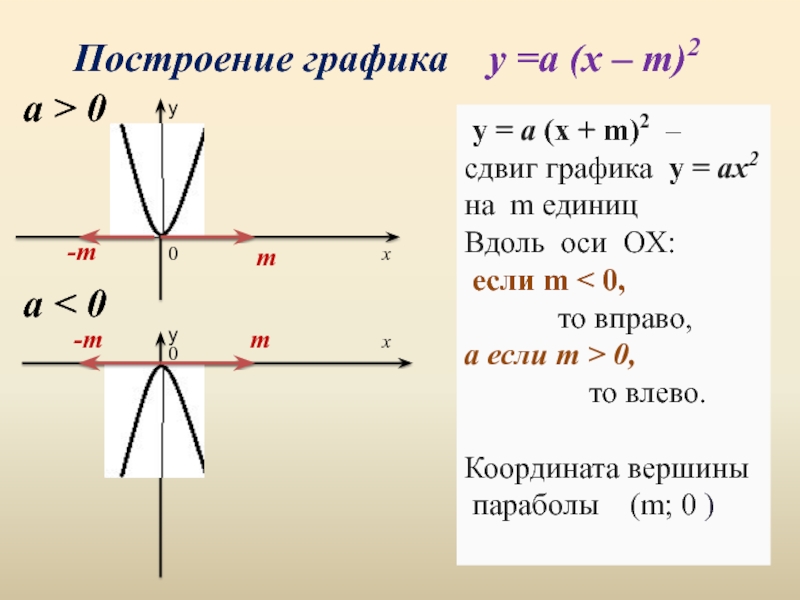
Слайд 14Построение графика y =a (x – m)2
у
у
х
х
y =
а (x + m)2 –
сдвиг графика y = аx2
на m единиц
Вдоль оси OХ:
если m < 0,
то вправо,
а если m > 0,
то влево.
Координата вершины
параболы (m; 0 )
сдвиг графика y = аx2
на m единиц
Вдоль оси OХ:
если m < 0,
то вправо,
а если m > 0,
то влево.
Координата вершины
параболы (m; 0 )
a > 0
a < 0
m
-m
-m
m
0
0
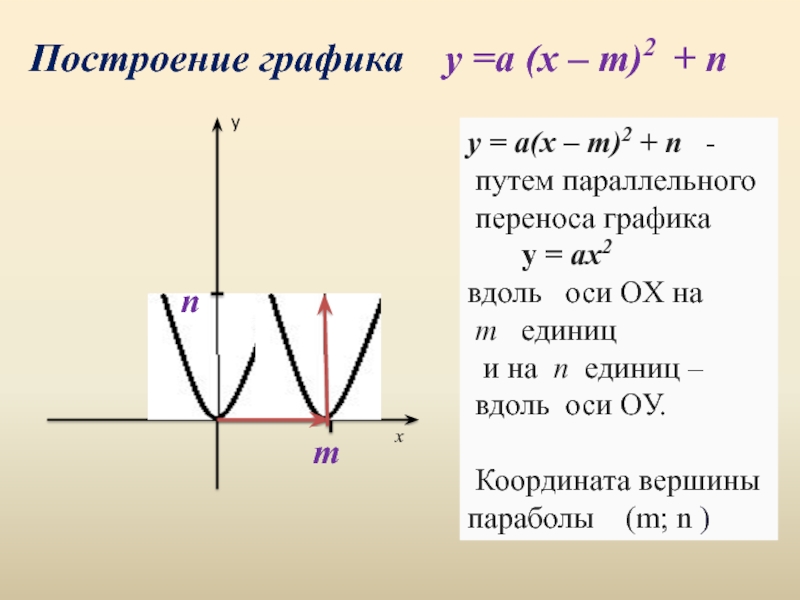
Слайд 16Построение графика y =a (x – m)2 + n
y
x
m
n
y
= a(x – m)2 + n -
путем параллельного
переноса графика
y = аx2
вдоль оси OХ на
m единиц
и на n единиц –
вдоль оси OУ.
Координата вершины параболы (m; n )
путем параллельного
переноса графика
y = аx2
вдоль оси OХ на
m единиц
и на n единиц –
вдоль оси OУ.
Координата вершины параболы (m; n )
Слайд 19
Используя шаблоны построить графики
функций, записать
координаты вершины параболы
I ряд
1)у = - 2 х2 +3 2) y = (x +4)2 3) y =0,5 (x – 3)2 – 4
II ряд
1)у = х2 - 2 2) y =- 0,5 (x + 3)2 3)y = 2(x +4)2 +3
III ряд
1)у =0,5 х2 +1 2) y = 2(x – 4 )2 3)y =- ( x – 2 )2 + 1
I ряд
1)у = - 2 х2 +3 2) y = (x +4)2 3) y =0,5 (x – 3)2 – 4
II ряд
1)у = х2 - 2 2) y =- 0,5 (x + 3)2 3)y = 2(x +4)2 +3
III ряд
1)у =0,5 х2 +1 2) y = 2(x – 4 )2 3)y =- ( x – 2 )2 + 1
Самостоятельная работа
Слайд 20 Ответы:
I ряд 1) у =
-2 х2 (0: 3)
2) у = х2 (-4; 0 )
3) у = - 0,5 х2 ( 3; - 4 )
II.ряд 1) у = х2 ( 0; -2)
2 ) у = -0,5 х2 (-3; 0 )
3) у = 2 х2 (- 4; 3 )
III ряд 1) .у = 0,5 х2 (0; 1 )
2) у = 2 х2 ( 4; 0 )
3) у = - х2 ( 2; 1 )
2) у = х2 (-4; 0 )
3) у = - 0,5 х2 ( 3; - 4 )
II.ряд 1) у = х2 ( 0; -2)
2 ) у = -0,5 х2 (-3; 0 )
3) у = 2 х2 (- 4; 3 )
III ряд 1) .у = 0,5 х2 (0; 1 )
2) у = 2 х2 ( 4; 0 )
3) у = - х2 ( 2; 1 )
шаблоны
Координаты вершины
параболы
Слайд 21Сообщение из истории развития функции
В математике понятие функции возникло
вместе
с понятием переменной величины,
введенной Р. Декартом и П. Ферма .
Определение функции впервые
сформулировал в 1718 г. швейцарский
математик И. Бернулли Новые открытия
расширили понятие функции. Большинство
естественных и общественных явлений,
процессов можно описать с помощью
функции. Исследуя свойства функции,
мы получаем новые возможности
познавать реальный мир. Сейчас
понятие функции вводится
согласно общей современной идее
функции, как соответствия.
Первым, кто подал эту идею в 1834 году,
Был русский математик Н.И. Лобачевский.
введенной Р. Декартом и П. Ферма .
Определение функции впервые
сформулировал в 1718 г. швейцарский
математик И. Бернулли Новые открытия
расширили понятие функции. Большинство
естественных и общественных явлений,
процессов можно описать с помощью
функции. Исследуя свойства функции,
мы получаем новые возможности
познавать реальный мир. Сейчас
понятие функции вводится
согласно общей современной идее
функции, как соответствия.
Первым, кто подал эту идею в 1834 году,
Был русский математик Н.И. Лобачевский.
1596-1650
1601-1665
Декарт
Ферма
Бернулли
1667-1748
Лобачевский
1794-1870
Слайд 22Если вращать параболу вокруг оси ее симметрии, то получается интересная поверхность,
которая называется параболоидом вращения.
Слайд 30У прожекторов зеркало обычно делается в форме параболоида Свойство параболы фокусировать
пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар
Слайд 34
Анкета самоанализа
На уроке я работал /а
активно / пассивно
Урок мне показался
коротким / длинным
Своей работой я па уроке
доволен / не доволен
За урок я
не устал / устал
Моё настроение
стало лучше / стало хуже
Материал урока мне был
понятен / не понятен
полезен / бесполезен
Рефлексия
