Грибовская Валентина Алексеевна,
учитель математики
МОБУ «СОШ №90»
р.п. Чунский Иркутской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Теория вероятностей на ЕГЭ - 2017
Содержание
- 1. Презентация Теория вероятностей на ЕГЭ - 2017
- 2. Кодификатор требований к уровню подготовки выпускников образовательных
- 3. Кодификатор элементов содержания по МАТЕМАТИКЕ для составления
- 4. Классическое определение вероятности Теоремы о вероятностях событийКлассическое
- 5. Тип задания по КТ. Задание на построение
- 6. ЕГЭ-2016 Ященко И.В. Решение задачи по теории
- 7. Задание 4 № 320196 ege.sdamgia.ruЗадача:При изготовлении подшипников диаметром 67
- 8. ЕГЭ-2016 Математика, И.В. Ященко
- 9. Пробник ЕГЭ Профильный г.
- 10. Пробник ЕГЭ февраль 2017 Вариант №
- 11. Прототип задания 4 markov_irk.@mail.ruЗадача: По отзывам покупателей
- 12. Досрочный ЕГЭ 31.03.17 Реальное задание №4
- 13. Прототип задания4 №501001 Сайт «Решу ЕГЭ»Задача: В
- 14. Прототип задания 4 № 501001 Сайт «Решу ЕГЭ»Задача:
- 15. Прототип задания №4
- 16. Прототип задания №4
- 17. Прототип задания4 markov_irk.@mail.ruЗадача: Бросили шесть
- 18. Прототип задания №4 markov_irk.@mail.ru Задача:
- 19. ЕГЭ – 2017. 30 тренировочных вариантов базовый
- 20. Прототип задания 4 markov_irk.@mail.ruЗадача:
- 21. Прототип задания 4 №320741Сайт «Решу ЕГЭ»Задача:
- 22. Прототип задания №4 markov_irk.@mail.ru Задача: В
- 23. Прототип задания4 № 282853 Сайт «Решу ЕГЭ»Задача: В
- 24. Прототип задания4 № 283461 Сайт «Решу ЕГЭ»Задача:
- 25. Из реальных вариантов ЕГЭЗадача: Фабрика выпускает
- 26. Из реальных вариантов ЕГЭРанее это задание было
- 27. ЕГЭ – 2017. 30 тренировочных вариантов базовый
- 28. Прототип задания4 №325905 Сайт «Решу ЕГЭ»
- 29. Прототип задания4 №325913 Сайт «Решу ЕГЭ»
- 30. Прототип задания4 №320210 Сайт «Решу ЕГЭ»
- 31. ЕГЭ–2017 ЯщенкоИ.В. 50 тренировочных
- 32. Трудные задания ЕГЭ–2017 Ященко И.В. 36
- 33. Прототип задания №4 https://ege.sdamgia.ruПроводится жеребьёвка Лиги Чемпионов. На
- 34. Прототип задания4 https://ege.sdamgia.ru Задача:
- 35. Трудные задания Прототип задания4 № 319353 Задача:
- 36. Трудные задания Прототип задания4 № 320172В
- 37. Трудные задания Прототип Задания4 № 320172В торговом
- 38. Удачи на ЕГЭ хочу я пожелать, Уверена
- 39. Используемые ресурсыЕГЭ. Математика. Профильный уровень : типовые
Слайд 1Теория вероятностей на ЕГЭ - 2017 Прототипы заданий №10 (базовый уровень) и
Слайд 2Кодификатор требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по
5. Уметь строить и исследовать простейшие математические модели
5.4 Моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий
Слайд 3Кодификатор элементов содержания по МАТЕМАТИКЕ для составления контрольных измерительных материалов для проведения единого государственного
6. Элементы комбинаторики, статистики и теории
вероятностей
Элементы комбинаторики
6.1.1 Поочередный и одновременный выбор
6.1.2 Формулы числа сочетаний и перестановок. Бином Ньютона
Элементы статистики
6.2.1 Табличное и графическое представление данных
6.2.2 Числовые характеристики рядов данных
Элементы теории вероятностей
6.3.1 Вероятности событий
6.3.2 Примеры использования вероятностей и статистики при решении прикладных задач
Слайд 4Классическое определение вероятности
Теоремы о вероятностях событий
Классическое определение. Вероятность события равняется отношению числа
где Р— вероятность события, 0≤ Р(А)≤1 , m— число благоприятствующих событию исходов, n — общее число равновозможных исходов.
Теорема: Вероятность суммы несовместных событий А и В равна сумме вероятностей этих событий Р(А+В) = Р(А) + Р(В).
Теорема: Вероятность суммы любых случайных событий А и В вычисляется по формуле Р(А+В) = Р(А) + Р(В) - Р(А ∙ В) .
Теорема: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
Слайд 5Тип задания по КТ. Задание на построение и исследование простейших математических
Характеристика задания. Несложная задача по теории вероятностей или статистике.
Комментарий. Для решения задачи достаточно уметь находить отношение числа благоприятных для наступления некоторого события исходов к числу всех равновозможных исходов.
Тип по КТ. Задание на построение и исследование простейших математических моделей: моделирование реальных ситуаций с использованием статистических и вероятностных методов, решение простейших комбинаторных задач методом перебора, а также с использованием известных формул; вычисление в простейших случаях вероятности событий на основе подсчета числа исходов.
Характеристика. Несложная задача по теории вероятностей или статистике.
Комментарий. Для решения задачи достаточно уметь находить отношение числа благоприятных для наступления некоторого события исходов к числу всех равновозможных исходов.
БАЗОВЫЙ
УРОВЕНЬ
ПРОФИЛЬНЫЙ УРОВЕНЬ
Слайд 6ЕГЭ-2016 Ященко И.В. Решение задачи по теории вероятностей Вариант 11, задача
Задача:
При изготовлении подшипников диаметром 69 мм вероятность того, что диаметр будет отличаться от заданного не более чем на 0,01 мм, равна 0,975. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 68,99 мм, или больше, чем 69,01мм.
Решение:
В данной задаче нужно найти вероятность превышения диаметра подшипника на 0,01 мм. Так как известна вероятность не превышения этого значения, то обратная вероятность будет равна
1-0,975=0,025.
Ответ: 0,025
Слайд 7Задание 4 № 320196 ege.sdamgia.ru
Задача:
При изготовлении подшипников диаметром 67 мм вероятность того, что
Решение:
По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Ответ: 0,035
Слайд 8 ЕГЭ-2016 Математика, И.В. Ященко 36 вариантов Вариант 8, Задание 4
Задача
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,95. Вероятность того, что окажется меньше 12 пассажиров, равна 0,6. Найдите вероятность того, что число пассажиров будет от 12 до 17.
Решение:
Выделим два события:
- в автобусе меньше 12 пассажиров;
- в автобусе от 12 до 17 пассажиров.
Сумма вероятностей этих несовместных событий есть не что иное, как вероятность того, что в автобусе окажется меньше 18 пассажиров, с известной вероятностью 0,95 (дана по условию задачи), т.е. можно записать равенство:
0,95 = Р(А) + Р(В).
Вероятность события А дана в задаче и равна 0,6, следовательно, вероятность события В равна
Р(В) = 0,95 - Р(А) = 0,95 – 0,6 = 0,35
Ответ: 0,35
Слайд 9
Пробник ЕГЭ Профильный г. Самара, 2017
сайт alexlarin.net:
Задача:
Из районного центра в деревню
Решение:
Будем использовать теорему о сумме двух несовместных событий.
Тогда искомая вероятность будет равна
P = 0,93 − 0,54 = 0,39.
Ответ: 0,39
Слайд 10Пробник ЕГЭ февраль 2017
Вариант № 193 сайт alexlarin.net:
Задача:
Считая, что интернет‐магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение:
По теореме об умножении вероятностей имеем
P = (1 − 0,7)∙(1 − 0,8) = 0,06.
Ответ: 0,06
Слайд 11
Прототип задания 4 markov_irk.@mail.ru
Задача: По отзывам покупателей Иван Иванович оценил надёжность двух
Решение:
(1-0,8)∙(1-0,9) =
= 0,2∙0,1 = 0,02.
Ответ: 0,02
Слайд 12Досрочный ЕГЭ 31.03.17
Реальное задание №4 сайт alexlarin.net:
Задача:
Перед началом
Решение:
Вероятность начинать матч равна 0,5.
Тогда вероятность начинать все три матча равна
P = 0,5∙0,5∙0,5 = 0,125.
Ответ: 0,125
Слайд 13Прототип задания4 №501001 Сайт «Решу ЕГЭ»
Задача:
В случайном эксперименте симметричную
Найдите вероятность того, что орёл выпадет ровно два раза.
Решение (I способ):
Можно перечислить все возможные случаи бросания монетки:
ООО, ООР, ОРО, ОРР,
РОО, РОР, РРО, РРР
и найти, в скольких из них орел выпал ровно два раза: ООР, ОРО, РОО. Тем самым, вероятность выпадения орла дважды равна 3 : 8 = 0,375.
(Этот подход затруднителен в случае большого числа бросаний монетки).
Слайд 14Прототип задания 4 № 501001 Сайт «Решу ЕГЭ»
Задача: В случайном эксперименте симметричную
Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: (II способ)
По формуле - следствию формулы Бернулли
где n = 3 - число бросаний монеты, m = 2 – число выпавших орлов, получим
Следовательно, искомая вероятность равна 3/8=0,375.
Ответ: 0,375
Слайд 15
Прототип задания №4 markov_irk.@mail.ru
Задача: В случайном эксперименте
Решение: (I способ)
Число благоприятных исходов m = 10:
ООРРР ОРОРР ОРРОР ОРРРО РООРР РОРОР РОРРО РРООР РРОРО РРРОО
из n = 32 равновозможных исходов.
Вероятность равна m/n =
= 10/32 = 0,3125
Ответ: 0,3125
Слайд 16
Прототип задания №4 markov_irk.@mail.ru
Задача: В случайном эксперименте
Решение: (II способ)
Число равновозможных исходов n = 25 = 32. Число благоприятных исходов
Вероятность равна
10/32 = 0,3125
Ответ: 0,3125
Слайд 17
Прототип задания4 markov_irk.@mail.ru
Задача: Бросили шесть монет. Какова вероятность того, что
Решение:
«Гербов» будет больше числа выпавших «решек» в следующих случаях:
ОООООО, ОООООР, ООООРР
Ответ: 0,34
Слайд 18
Прототип задания №4 markov_irk.@mail.ru
Задача: Бросили шесть монет. Какова вероятность
Решение:
«Гербов» будет вдвое больше числа выпавших «решек» в случае выпадения четырех «гербов» и двух «решек»: ООООРР, тогда
Ответ: 0,234
Слайд 19ЕГЭ – 2017. 30 тренировочных вариантов базовый уровень / под ред.
Задача:
На борту самолета 25 мест рядом с запасными выходами и 15 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Б. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Б. достанется удобное, если всего в самолете 500 мест.
Решение:
Искомая вероятность находится согласно классическому определению вероятности, то есть,
Ответ: 0,08
Слайд 20
Прототип задания 4 markov_irk.@mail.ru
Задача: Агрофирма закупает куриные яйца в
60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 40% яиц высшей категории.
Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение:
Пусть х — искомая вероятность того, что куплено яйцо, произведенное в первом хозяйстве. Тогда 1- х — вероятность того, что куплено яйцо, произведенное во втором хозяйстве. По формуле полной вероятности имеем:
0,6х + (1-х)∙0,4 = 0,55
0,2х = 0,15; х = 0,75
Ответ: 0,75
Слайд 21
Прототип задания 4 №320741Сайт «Решу ЕГЭ»
Задача: Агрофирма закупает куриные яйца в
Решение:
Пусть х — искомая вероятность того, что куплено яйцо, произведенное в первом хозяйстве. Тогда 1- х — вероятность того, что куплено яйцо, произведенное во втором хозяйстве. По формуле полной вероятности имеем:
0,6х + (1-х)∙0,7 = 0,65
- 0,1х = - 0,05; х = 0,5
Ответ: 0,5
Слайд 22
Прототип задания №4 markov_irk.@mail.ru
Задача:
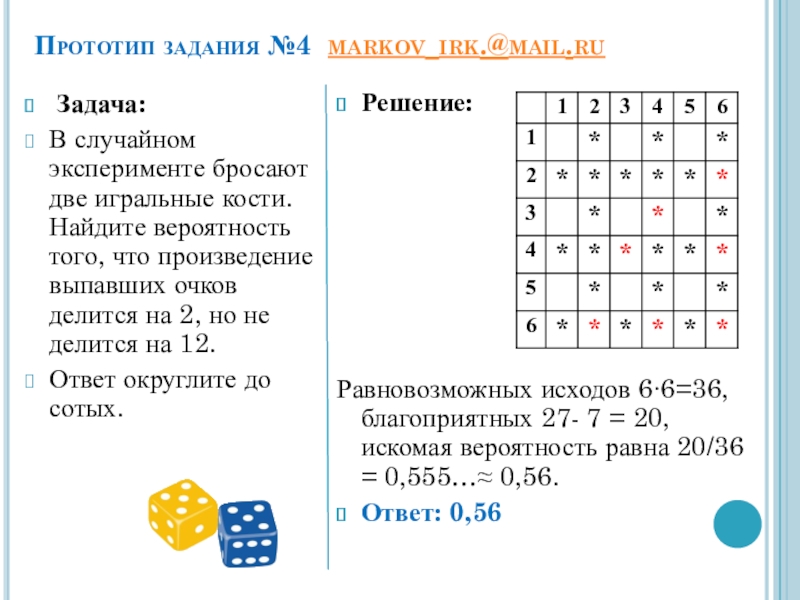
В случайном эксперименте бросают две игральные
Ответ округлите до сотых.
Решение:
Равновозможных исходов 6∙6=36, благоприятных 27- 7 = 20, искомая вероятность равна 20/36 = 0,555…≈ 0,56.
Ответ: 0,56
Слайд 23Прототип задания4 № 282853 Сайт «Решу ЕГЭ»
Задача: В случайном эксперименте бросают две
Решение:
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5:
2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6∙6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
5/36 = 0,138…≈ 0,14.
Ответ: 0,14
Слайд 24Прототип задания4 № 283461 Сайт «Решу ЕГЭ»
Задача:
В случайном эксперименте
Результат округлите до сотых.
Решение:
Количество исходов, при которых в результате броска игральных костей выпадет 6 очков, равно 10:
1 + 1 + 4, 1 + 4 + 1, 4 + 1 + 1,
1 + 2 + 3, 1 + 3 + 2, 3 + 1 + 2,
3 + 2 + 1, 2 + 1 + 3, 2 + 3 + 1,
2 + 2 + 2.
Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6 · 6 · 6 = 216. Следовательно, вероятность того, что в сумме выпадет 6 очков, равна
Ответ: 0,05
Слайд 25Из реальных вариантов ЕГЭ
Задача:
Фабрика выпускает сумки. В среднем 8
Решение:
В среднем без дефектов выпускают 92 сумки из каждых 100, поэтому искомая вероятность равна 92/100 = 0,92.
Ответ: 0, 92
Слайд 26Из реальных вариантов ЕГЭ
Ранее это задание было сформулировано следующим образом.
Фабрика выпускает
Решение:
По условию из любых
100 + 8 = 108 сумок
в среднем 100 качественных сумок.
Значит, вероятность того, что купленная сумка окажется качественной, равна
Ответ: 0,93
Слайд 27ЕГЭ – 2017. 30 тренировочных вариантов базовый уровень / под ред.
Задача:
В большой партии насосов в среднем на каждые 144 исправных приходится 6 неисправных насосов. Найдите вероятность того, что случайно выбранный насос окажется исправным.
Решение:
По условию из любых
144 + 6 = 150 насосов
в среднем 144 исправных насосов.
Значит, вероятность того, что, случайно выбранный насос окажется исправным
равна 144/150 = 0,96.
Ответ: 0,96
Слайд 28
Прототип задания4 №325905 Сайт «Решу ЕГЭ»
Задача: За круглый стол на 5
Решение:
Пусть первой за стол сядет девочка, тогда рядом с ней есть два места, на каждое из которых претендует 4 человека, из которых только одна девочка. Таким образом, вероятность, что девочки будут сидеть рядом, равна
Ответ: 0,5
Слайд 29
Прототип задания4 №325913 Сайт «Решу ЕГЭ»
Задача: За круглый стол на
Решение:
Пусть первой за стол сядет девочка, тогда рядом с ней есть два места, на каждое из которых претендует 8 человек, из которых только одна девочка. Таким образом, вероятность того, что девочки будут сидеть рядом равна 2:8=0,25.
А вероятность того, что девочки не будут сидеть рядом, равна 1- 0,25 = 0,75.
Ответ: 0,75
Слайд 30
Прототип задания4 №320210 Сайт «Решу ЕГЭ»
Задача: Вероятность того, что батарейка бракованная,
Решение:
Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.
Ответ: 0,8836
Слайд 31
ЕГЭ–2017 ЯщенкоИ.В. 50 тренировочных вариантов Задание №4
Автоматическая линия изготавливает батарейки.
Решение:
Ситуация, при которой батарейка будет забракована, может сложиться в результате событий:
A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована.
Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем:
Р(А+В) = Р(А) + Р(В) =
0,02∙0,99 + 0,98∙0,01=
0, 0198 + 0,098 = 0,0296.
Ответ: 0,0296
Слайд 32Трудные задания ЕГЭ–2017 Ященко И.В.
36 вариантов профильный уровень Вариант19
Задача: При
Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем — 0,9. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,96?
Решение: Вероятность уцелеть после ряда последовательных промахов:
Р(1) = 1 – 0,3 = 0,7
Р(2) = Р(1)∙(1-0,9) = 0,07
Р(3) = Р(2)∙(1-0,9)=0,007
1 – 0,96 = 0,04
0,007 < 0,04, значит достаточно трех выстрелов.
Ответ: 3
Слайд 33Прототип задания №4 https://ege.sdamgia.ru
Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь
Решeние:
По результатам первой жеребьёвки команда «Барселона» находится в одной из 8 групп. Вероятность того, что команда «Зенит» окажется в той же игровой группе равна одной восьмой.
Ответ: 0,125
Слайд 34
Прототип задания4 https://ege.sdamgia.ru
Задача:
На рок-фестивале выступают группы —
Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии?
Результат округлите до сотых.
Решeние:
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих
(Д — Дания, Ш — Швеция, Н — Норвегия):
...Д...Ш...Н..., ...Д...Н...Ш..., ...Ш...Н...Д..., ...Ш...Д...Н..., ...Н...Д...Ш..., ...Н...Ш...Д...
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
Ответ: 0,33
Слайд 35Трудные задания Прототип задания4 № 319353
Задача: Две фабрики выпускают одинаковые стекла
Решeние:
Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,0135 + 0,0055 = 0,019.
Ответ: 0,019
Слайд 36Трудные задания Прототип задания4 № 320172
В торговом центре два одинаковых
Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3.
Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решeние: (I способ)
Рассмотрим события
А - кофе закончится в первом автомате,
В - кофе закончится во втором. Тогда
A· B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном .
По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.
События A и B совместные, вероятность суммы равна
P(A + B) = P(A) + P(B) − P(A· B) =
= 0,3 + 0,3 − 0,12 = 0,48.
Значит, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
Ответ: 0,52
Слайд 37Трудные задания Прототип Задания4 № 320172
В торговом центре два одинаковых автомата
Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение: (II способ)
Вероятность того, что кофе останется в первом автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате, равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A· B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52.
Ответ: 0,52
Слайд 38Удачи на ЕГЭ хочу я пожелать, Уверена я в вас, сдадим ЕГЭ
Успешной сдачи ЕГЭ!
Слайд 39Используемые ресурсы
ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36
ЕГЭ-2017. Математика. Профильный уровень. 50 тренировочных вариантов / под ред. И. В. Ященко. — М., 2017
ЕГЭ-2017: Математика: 30 тренировочных вариантов экзаменационных работ для подготовки к ЕГЭ: базовый уровень / под ред. И. В. Ященко. — М. : АСТ, 2016.
ege.sdamgia.ru
alexlarin.net:
Сайт «Решу ЕГЭ»
markov_irk.@mail.ru