- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение неравенств методом интервалов.
Содержание
- 1. Презентация Решение неравенств методом интервалов.
- 2. РЕШЕНИЕ НЕРАВЕНСТВАРешением неравенства с неизвестным х называют
- 3. РАССМОТРИМ СПОСОБ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА:(х - х1)
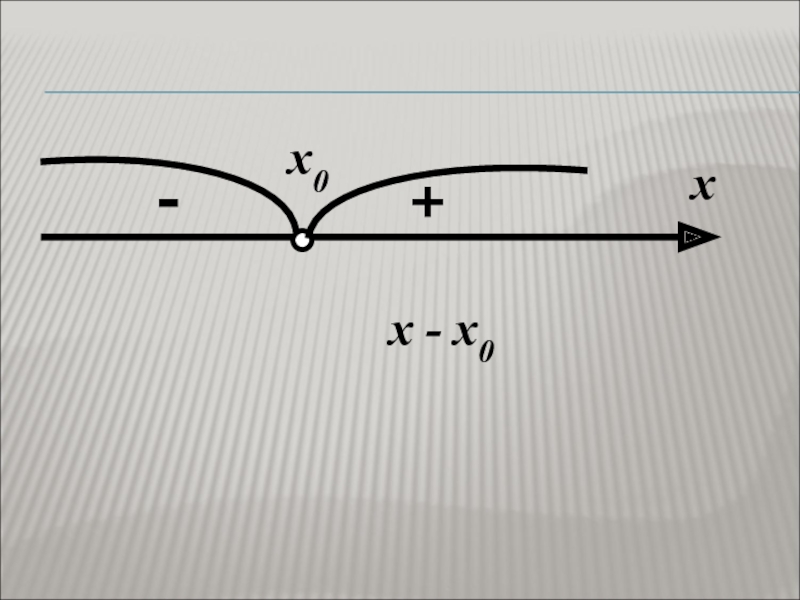
- 4. xx0х - x0+-
- 5. ПУСТЬ ТРЕБУЕТСЯ РЕШИТЬ НЕРАВЕНСТВО:(х - х1) (х
- 6. РАССМОТРИМ МНОГОЧЛЕН А(Х) = (Х - Х1)
- 7. МЕТОД ИНТЕРВАЛОВНа оси абсцисс отмечают точки х1;х2;х3;Над
- 8. ПРИМЕР 1Решим неравенство: (х-2)(х-3)(х-4)>0.Отметим на оси ОХ
- 9. ПРИМЕР 2Решим неравенство: (2-х)(х2-4х+3)(х+1)>0Разложим квадратный трехчлен на множители:(2-х)(х-3)(х-1)(х+1)>0умножим обе части неравенства на -1(х-(-1))(х-1)(х-2)(х-3)
- 10. ПРИМЕР3Решим неравенство:(х-1)(х-3)(х2+х+1)
- 11. ПРИМЕР 4Решим неравенство:(х-1)3(х-2)2(х-3)4(х-4)
РЕШЕНИЕ НЕРАВЕНСТВАРешением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое неравенство.Решить неравенство – значит найти все его решения или показать, что их нет.
Слайд 2РЕШЕНИЕ НЕРАВЕНСТВА
Решением неравенства с неизвестным х называют число, при подстановке которого
в это неравенство вместо х получается верное числовое неравенство.
Решить неравенство – значит найти все его решения или показать, что их нет.
Решить неравенство – значит найти все его решения или показать, что их нет.
Слайд 3РАССМОТРИМ СПОСОБ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА:
(х - х1) (х - х2)· …
· (х - хn) > 0
и
(х - х1) (х - х2)· … · (х - хn) < 0,
где
х1 < х2 < … < хn , n – натуральное число
( n ≥1).
и
(х - х1) (х - х2)· … · (х - хn) < 0,
где
х1 < х2 < … < хn , n – натуральное число
( n ≥1).
Слайд 5ПУСТЬ ТРЕБУЕТСЯ РЕШИТЬ НЕРАВЕНСТВО:
(х - х1) (х - х2)(х – х3)
> 0
Или неравенство
(х - х1) (х - х2)(х – х3) < 0, где х1 < х2 < х3
Или неравенство
(х - х1) (х - х2)(х – х3) < 0, где х1 < х2 < х3
(-∞;x1) (x1 ;x2) (x2 ;x3) (x3;+∞)
x1
x2
x3
x
Слайд 6РАССМОТРИМ МНОГОЧЛЕН А(Х) = (Х - Х1) (Х - Х2)(Х – Х3)
+
+
-
-
2. А(х)<0,при x ϵ (-∞;x1)U (x2 ;x3)
1. А(х)>0, при x ϵ (x1 ;x2)U(x3;+∞)
Слайд 7МЕТОД ИНТЕРВАЛОВ
На оси абсцисс отмечают точки х1;х2;х3;
Над интервалом (х3;+∞) ставят знак
«+»
Над интервалом (х2;х3) ставят знак «-»
Над интервалом (х1;х2) ставят знак «+»
Над интервалом (-∞;х1) ставят знак «-»
Решение неравенства
Над интервалом (х2;х3) ставят знак «-»
Над интервалом (х1;х2) ставят знак «+»
Над интервалом (-∞;х1) ставят знак «-»
Решение неравенства
*
+
+
-
-
(х - х1) (х - х2)· … · (х - хn) > 0
x ϵ (x1 ;x2)U(x3;+∞)
(х - х1) (х - х2)· … · (х - хn) > 0
x ϵ (-∞;x1)U (x2 ;x3)
Слайд 8ПРИМЕР 1
Решим неравенство: (х-2)(х-3)(х-4)>0.
Отметим на оси ОХ точки 2;3;4
Над интервалами(4;+∞);(3;4);(2;3);(-∞;2) справа
налево поставим поочередно знаки «+»; «-».
Ответ:(2;3)U(4; +∞)
Ответ:(2;3)U(4; +∞)
+
-
+
-
Слайд 9ПРИМЕР 2
Решим неравенство: (2-х)(х2-4х+3)(х+1)>0
Разложим квадратный трехчлен на множители:(2-х)(х-3)(х-1)(х+1)>0
умножим обе части неравенства
на -1
(х-(-1))(х-1)(х-2)(х-3)<0
Отметим на оси ОХ точки-1;1;2;3
Ответ:(-1;1)U(2;3)
(х-(-1))(х-1)(х-2)(х-3)<0
Отметим на оси ОХ точки-1;1;2;3
Ответ:(-1;1)U(2;3)
+
-
+
-
+
Слайд 11ПРИМЕР 4
Решим неравенство:(х-1)3(х-2)2(х-3)4(х-4)
состоит в следующем:
Отметим на оси ОХ точки 1;2;3;4, а затем в каждом интервале исследуем знак многочлена А(х)= (х-1)3(х-2)2(х-3)4(х-4)
Ответ:(1;2)U (2;3) U(3;4).
Отметим на оси ОХ точки 1;2;3;4, а затем в каждом интервале исследуем знак многочлена А(х)= (х-1)3(х-2)2(х-3)4(х-4)
Ответ:(1;2)U (2;3) U(3;4).
+
-
-
+
-
