- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Производная и первообразная на ЕГЭ
Содержание
- 1. Презентация Производная и первообразная на ЕГЭ
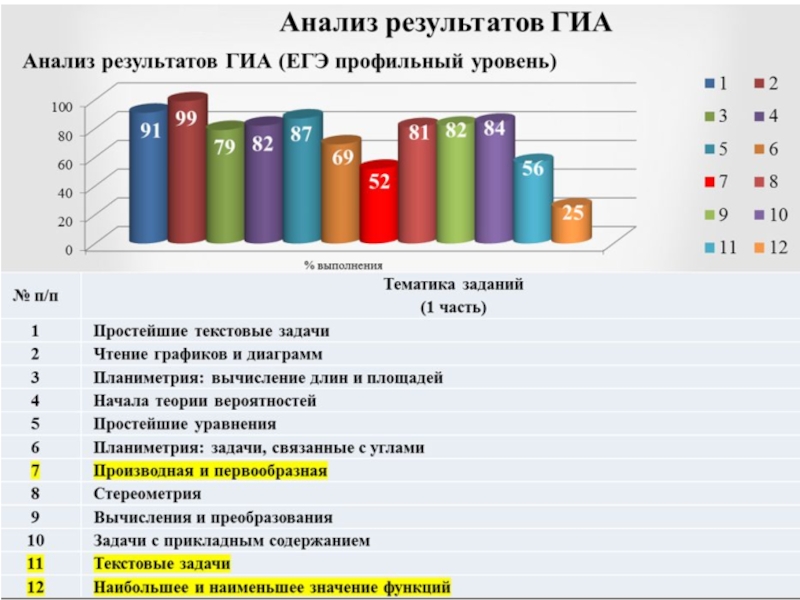
- 2. 7.Производная и первообразная12.Наибольшее и наименьшее значение функций18 (C6).Задача с параметромЗадания ЕГЭ (профильный уровень)
- 3. Проверяемые требования (умения) в заданиях №7 и
- 4. Для этого необходимо:● Уметь определять свойства функции
- 5. Слайд 5
- 6. Слайд 6
- 7. Геометрический смысл производной
- 8. ух011аbОпределите по графику функции у = f
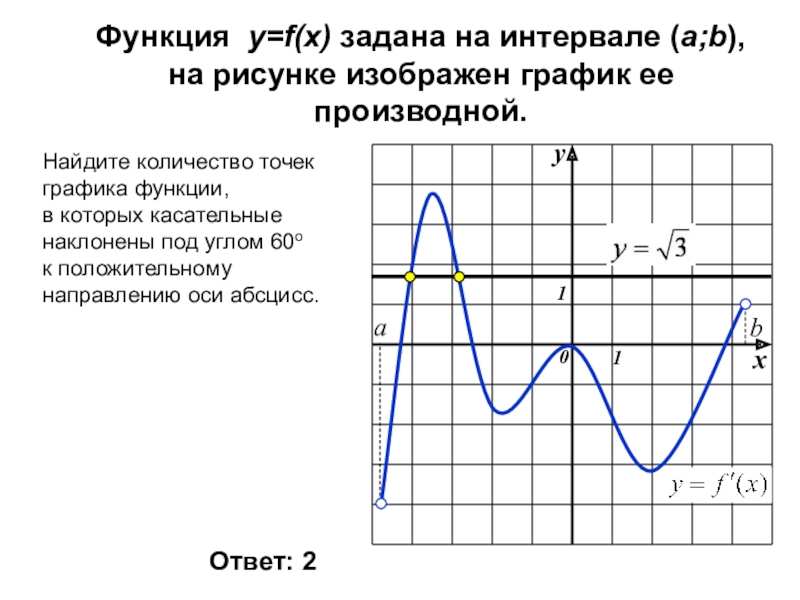
- 9. Функция y=f(x) задана на интервале (a;b), на
- 10. Функция y=f(x) задана на интервале (a;b), на
- 11. Функция y=f(x) задана на интервале (a;b), на
- 12. Физический смысл производной
- 13. Две материальные точки
- 14. Пусть количество вещества,
- 15. Тело, подброшенное вверх, движется по закону s(t)
- 16. Применение производной к исследованию функций
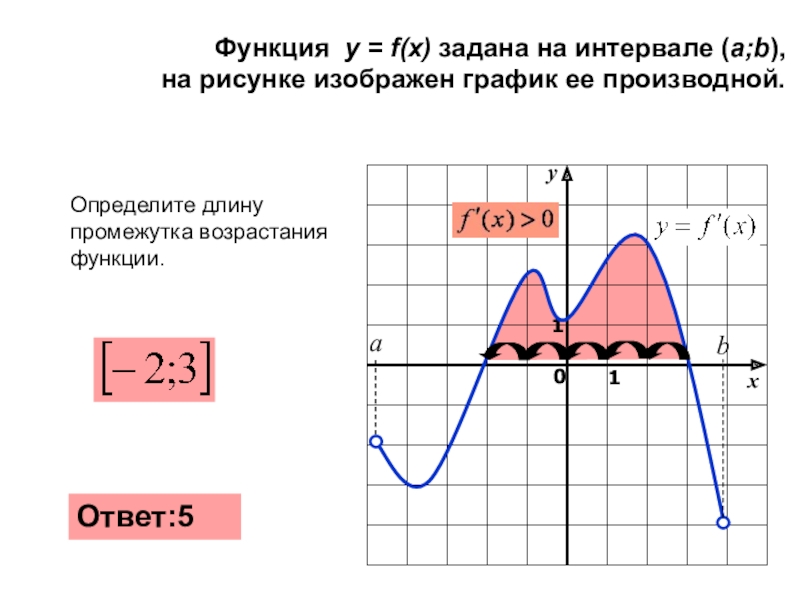
- 17. Ответ:5Определите длину промежутка возрастания функции.аb
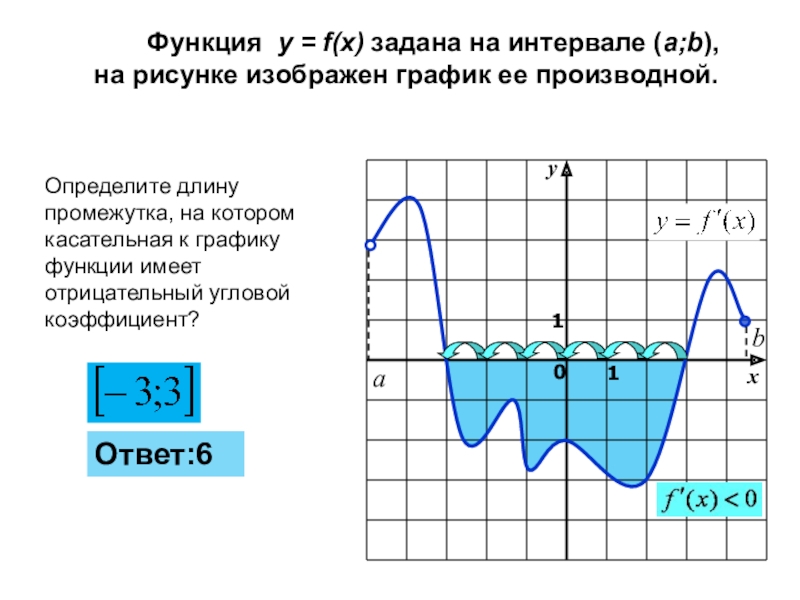
- 18. Определите длину промежутка, на котором касательная к графику функции имеет отрицательный угловой коэффициент? Ответ:6
- 19. Функция y=f(x) задана на интервале (a;b), на
- 20. Задание № 12 В
- 21. Найдите наименьшее значение функции на отрезке [
- 22. Критических точек нет.Тогда наибольшее значение функция будет
- 23. Найдите наибольшее значение функции на отрезке [
- 24. Найдите наибольшее значение
- 25. Первообразная и интеграл
- 26. Задача 1 На
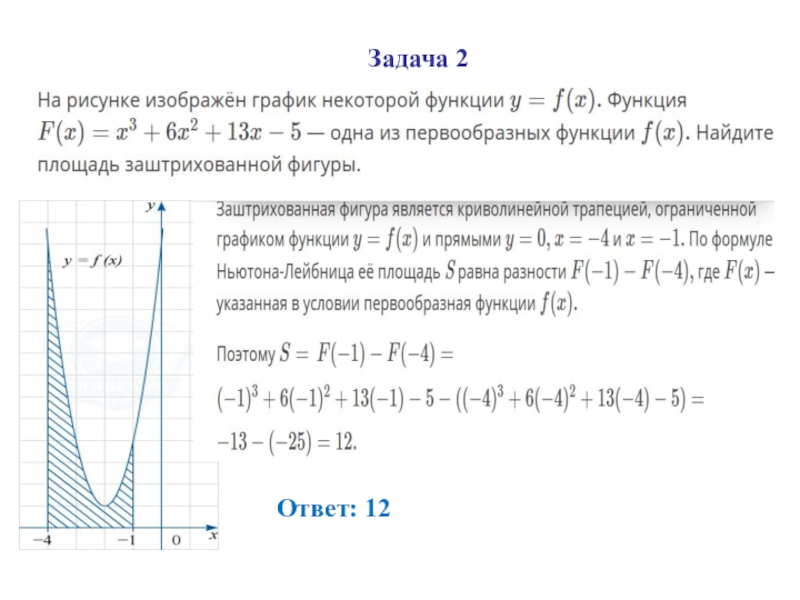
- 27. Задача 2 Ответ: 12
- 28. Задача 3 На рисунке
- 29. Задание части «С»
- 30. При каких значениях параметра а уравнение имеет
- 31. При каких значениях параметра а уравнение имеет
- 32. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 27.Производная и первообразная
12.Наибольшее и наименьшее значение функций
18 (C6).Задача с параметром
Задания ЕГЭ
Слайд 3Проверяемые требования (умения)
в заданиях №7 и №12 по кодификатору
3.1.
3.2. Вычислять производные и первообразные элементарных функций.
3.3. Исследовать в простейших случаях функции
на монотонность, находить наибольшие и наименьшие значения функций.
Слайд 4Для этого необходимо:
● Уметь определять свойства функции по её графику (промежутки
●Уметь определять свойства функции по информации о производной функции (которая будет содержаться в графике производной);
● Знать геометрический и физический смыслы производной;
● Уметь работать с уравнением касательной.
Слайд 8у
х
0
1
1
а
b
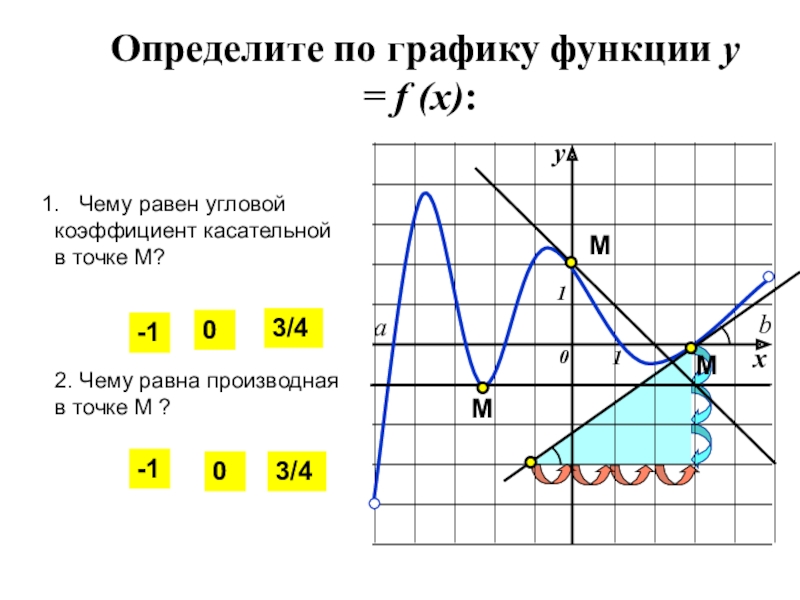
Определите по графику функции у = f (x):
Чему равен угловой
в точке М?
2. Чему равна производная
в точке М ?
-1
-1
0
0
3/4
3/4
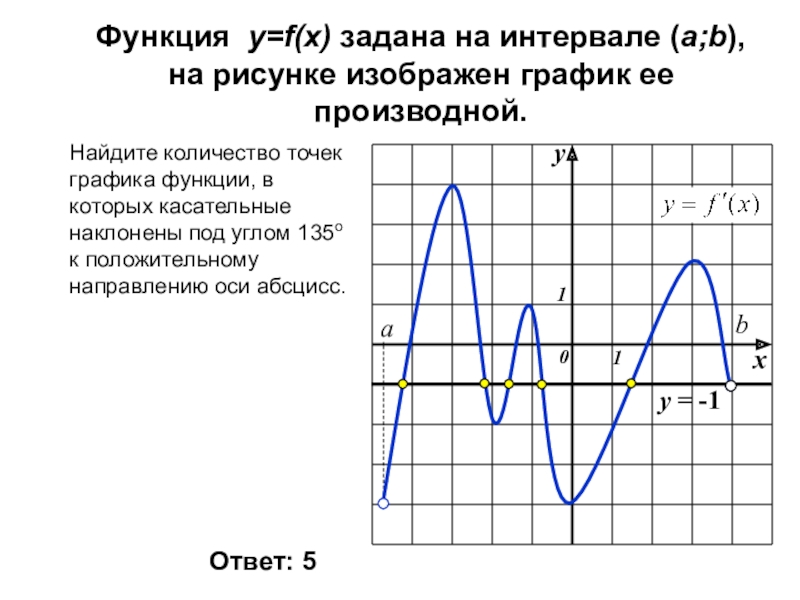
Слайд 9Функция y=f(x) задана на интервале (a;b),
на рисунке изображен график ее производной.
Найдите
Ответ: 5
у
х
0
1
1
а
b
у = -1
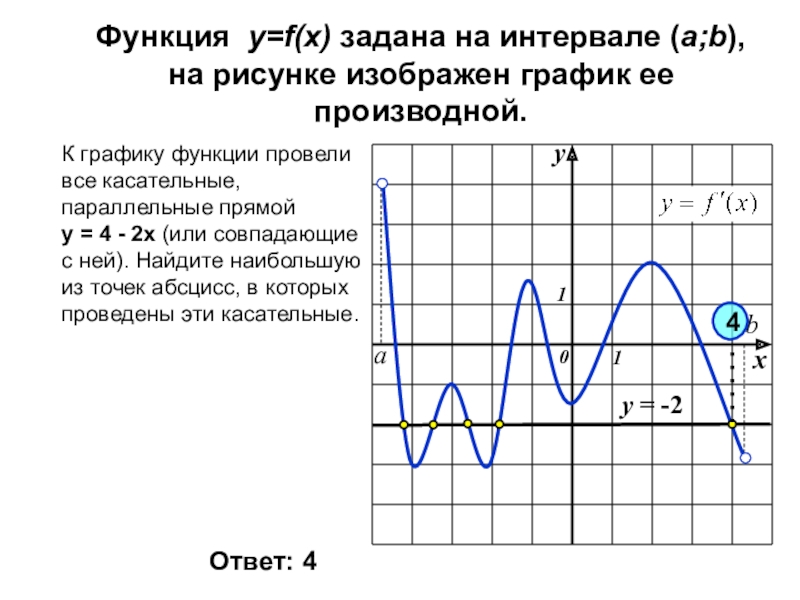
Слайд 10Функция y=f(x) задана на интервале (a;b),
на рисунке изображен график ее производной.
у
х
0
1
1
а
b
К
Ответ: 4
4
у = -2
Слайд 11Функция y=f(x) задана на интервале (a;b),
на рисунке изображен график ее производной.
Найдите
у
х
0
1
1
а
b
Ответ: 2
Слайд 13 Две материальные точки движутся прямолинейно
по законам s1(t) = 1 - 6t + 2,5t 2 и s2(t) = -3+ 2t + 0,5t 2 .
Определить, в какой момент времени скорости их
будут равны.
Ответ: при t = 2 с
РЕШЕНИЕ.
ЗАДАЧА №1
Слайд 14 Пусть количество вещества, вступившего
в химическую реакцию, задается зависимостью
р( t ) = 0,5t 2 + 3t –3 (моль).
Найти скорость химической реакции через 3 секунды.
ЗАДАЧА №2
РЕШЕНИЕ.
1) v( t ) = p`( t ) = t + 3,
2) v(3) = p`(3) = 3 + 3 = 6(моль/сек)
Ответ: 6 моль / сек
Слайд 15Тело, подброшенное вверх, движется по закону
s(t) = 4+ 8t
1) Скорость тела в начальный момент времени.
2) Наибольшую высоту подъёма тела.
РЕШЕНИЕ.
2) t= 0, v(0) = s`(0) = 8 м/с – скорость
тела в начальный момент времени
1) v (t) = s` (t) = 8 – 10t - скорость тела;
3) s (0,8)= 4+ 8·0,8 – 5· 0,64 =7,2 м – максимальная высота броска тела.
Ответ: 8 м/с ; 7,2 м .
ЗАДАЧА №3
Слайд 18Определите длину промежутка, на котором касательная к графику функции имеет отрицательный
Ответ:6
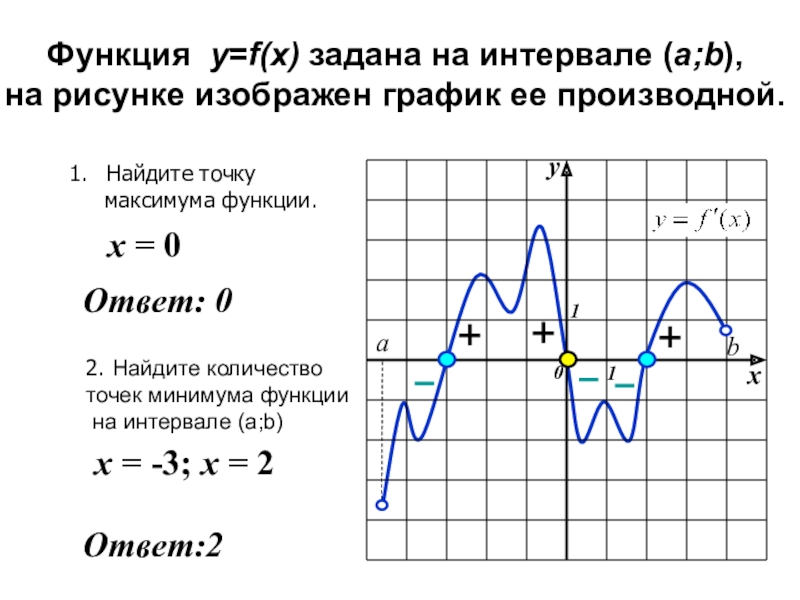
Слайд 19Функция y=f(x) задана на интервале (a;b),
на рисунке изображен график ее производной.
у
х
0
1
1
b
а
Найдите
максимума функции.
2. Найдите количество
точек минимума функции
на интервале (a;b)
х = 0
х = -3; х = 2
Ответ:2
Ответ: 0
Слайд 20Задание № 12
В заданиях проверяется умение использовать
Полезно знать: функция, непрерывная на отрезке, достигает свои наименьшее и наибольшее значения на этом отрезке либо в точке экстремума, либо на границе этого отрезка.
Алгоритм:
1. Найти производную заданной функции.
2. Найти точки на отрезке, где производная равна нулю
или не существует.
3. Вычислить значения функции в этих точках и в граничных
точках.
4. Выбрать наибольшее или наименьшее значения.
Слайд 21Найдите наименьшее значение функции
на отрезке [ 1; 9 ]
Найдем критические
Выбрать наименьшее
из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 22Критических точек нет.
Тогда наибольшее значение функция будет принимать в одном из
Найдите наибольшее значение функции
y = 10sinx – x + 7 на отрезке
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
Слайд 23Найдите наибольшее значение функции
на отрезке [ 3; 10 ]
Найдем критические
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
1) Первое число меньше 1, т.к. знаменатель e4 > 5.
2) Второе число – отрицательноe.
3) Значит, наибольшее число 1.
1
Слайд 24 Найдите наибольшее значение функции
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить время на вычислениях значений функции в концах отрезка.
y = 5ln(x+5) – 5x
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках
и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее.
0
Можно рассуждать иначе
Запишем функцию в удобном для дифференцирования виде
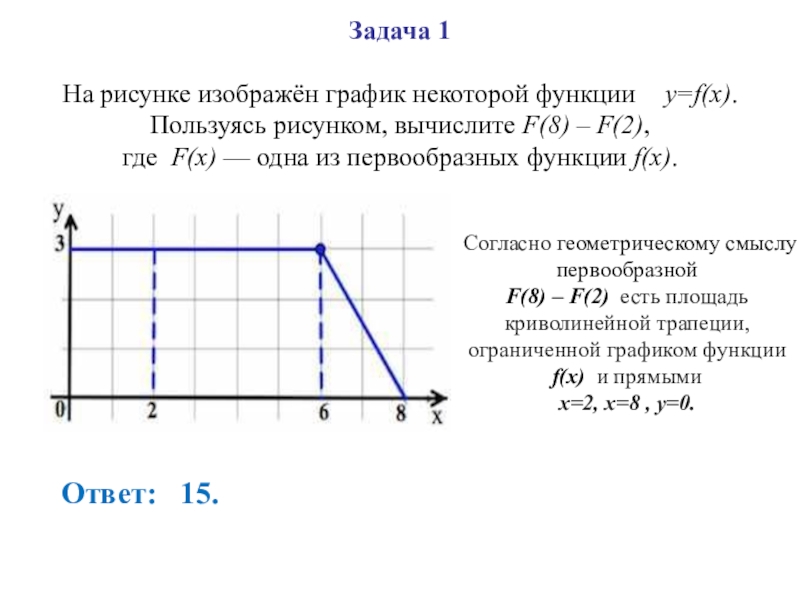
Слайд 26 Задача 1 На рисунке изображён график некоторой функции y=f(x). Пользуясь рисунком, вычислите F(8)
Согласно геометрическому смыслу первообразной
F(8) – F(2) есть площадь криволинейной трапеции, ограниченной графиком функции f(x) и прямыми
x=2, x=8 , y=0.
Ответ: 15.
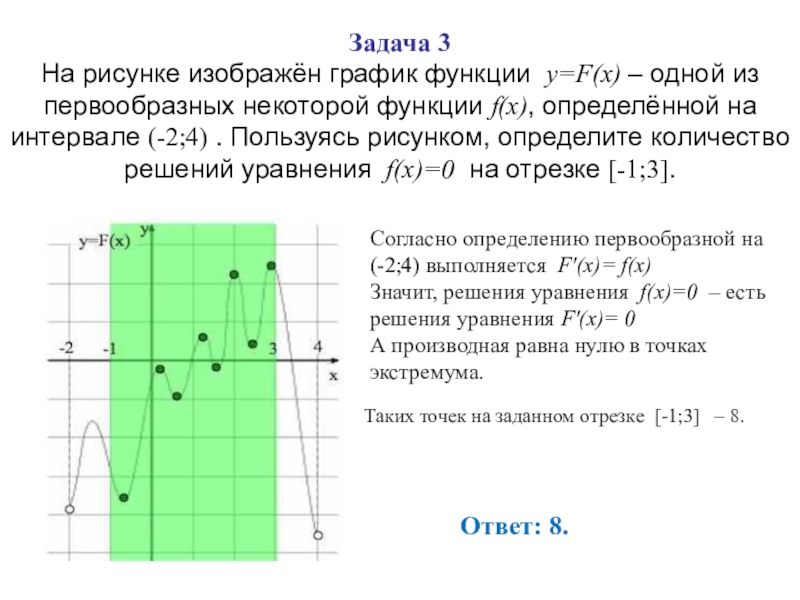
Слайд 28 Задача 3 На рисунке изображён график функции y=F(x) – одной из первообразных некоторой функции f(x),
Согласно определению первообразной на (-2;4) выполняется F'(x)= f(x)
Значит, решения уравнения f(x)=0 – есть решения уравнения F'(x)= 0
А производная равна нулю в точках экстремума.
Ответ: 8.
Таких точек на заданном отрезке [-1;3] – 8.
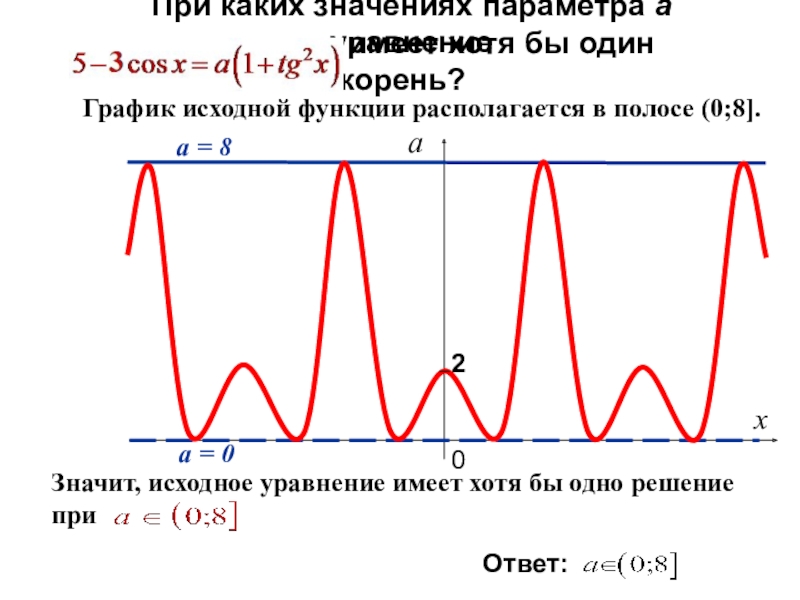
Слайд 30При каких значениях параметра а уравнение
имеет хотя бы один
Запишем данное уравнение в виде:
Исследуем функцию a (t) с помощью производной :
Значения функции на концах:
Решение.
.
.
Слайд 31При каких значениях параметра а уравнение
имеет хотя бы один
а = 8
а = 0
График исходной функции располагается в полосе (0;8].
Значит, исходное уравнение имеет хотя бы одно решение при












![Презентация Производная и первообразная на ЕГЭ Найдите наименьшее значение функции на отрезке [ 1; 9 ]Найдем критические Найдите наименьшее значение функции на отрезке [ 1; 9 ]Найдем критические точки, которые принадлежат заданному отрезку.Выбрать наименьшее](/img/thumbs/bc20ba070447e2a00d8fdfc40be0f60e-800x.jpg)

![Презентация Производная и первообразная на ЕГЭ Найдите наибольшее значение функции на отрезке [ 3; 10 ]Найдем критические Найдите наибольшее значение функции на отрезке [ 3; 10 ]Найдем критические точки, которые принадлежат заданному отрезку.Выбрать наибольшее](/img/thumbs/4688ac84c9055a39aa263fabc365eee3-800x.jpg)