- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Производная и её применение
Содержание
- 1. Презентация Производная и её применение
- 2. «Музыка может возвышать или умиротворять душу,Живопись
- 3. Производная и Её применение
- 4. Определение функции Соответствие, при котором каждому
- 5. Определение производной функции Производной функции f(x)
- 6. Правила вычисления производной Пусть функции
- 7. Физический смысл производнойЗначение производной функции y
- 8. Как вычислить скорость движения материальной точки с
- 9. Как вычислить силу тока, если известен закон
- 10. Как вычислить мощность, если известен закон производимой
- 11. Задачи Группа 1: Движение материальной точки
- 12. Задача: В координатной плоскости изображён график зависимости
- 13. ФИЗКУЛЬТМИНУТКА
- 14. в чем состоит экономический смысл производной?Если непрерывная
- 15. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИНайти область определения функции. (Указать
- 16. УСТНЫЙ ОПРОСДостаточный признак возрастания функции.Достаточный признак убывания
- 17. Достаточный признак возрастания функции Если функция
- 18. Достаточный признак убывания функции Если функция
- 19. Необходимое условие экстремума (Теорема Ферма)
- 20. Признак максимума функцииЕсли в точке х0 производная
- 21. Признак минимума функцииЕсли в точке х0 производная
- 22. Исследовательская работаФункция полных издержек локомотивного депо города
- 23. Оцените вашу работу на урокеПродолжите фразу: Урок
- 24. Исследуя функцию с помощью производной, я Смог:
- 25. ИТОГ УРОКАМы еще раз увидели взаимосвязь между
- 26. ДОМАШНЕЕ ЗАДАНИЕП.п. 49-52 , №№ 971 (2), 981 (1)
- 27. Спасибо за активное участие на уроке!!!
«Музыка может возвышать или умиротворять душу,Живопись – радовать глаз,Поэзия – пробуждать чувства,Философия – удовлетворять потребности разума, Инженерное дело –совершенствовать материальную сторону жизни людей. Математика способна достичь всех этих целей!»Морис Клайн
Слайд 2«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия –
пробуждать чувства,
Философия – удовлетворять
потребности разума,
Инженерное дело –совершенствовать материальную сторону жизни людей.
Математика способна достичь всех этих целей!»
Морис Клайн
Философия – удовлетворять
потребности разума,
Инженерное дело –совершенствовать материальную сторону жизни людей.
Математика способна достичь всех этих целей!»
Морис Клайн
Слайд 4Определение функции
Соответствие, при котором каждому значению независимой переменной
(аргументу функции) сопоставляется единственное значение зависимой переменной, называется функцией.
Слайд 5Определение производной функции
Производной функции f(x) в точке Х0 ,
называется отношение приращения функции к приращению аргумента, при условии что приращение аргумента стремиться к нулю.
*
Слайд 6Правила вычисления производной
Пусть функции f и g
дифференцируемы в точке x0 , тогда
Правило 1 ( f + g)′ = f ′ + g′
Правило 2 ( f ⋅ g)′ = f ′ ⋅ g + f ⋅ g′
Правило 3
Правило 4 (c ⋅ g)′ = c ⋅ ( g)′
Правило 5 ( f (g(x)))′ = f ′ (g(x))⋅ g′ (x)
Правило 1 ( f + g)′ = f ′ + g′
Правило 2 ( f ⋅ g)′ = f ′ ⋅ g + f ⋅ g′
Правило 3
Правило 4 (c ⋅ g)′ = c ⋅ ( g)′
Правило 5 ( f (g(x)))′ = f ′ (g(x))⋅ g′ (x)
Слайд 7Физический смысл производной
Значение производной функции y = f (x) в
точке x0 ,есть скорость изменении функции y в данный момент времени
Слайд 8Как вычислить скорость движения материальной точки с помощью производной?
Пусть S =
S(t) – закон движения материальной точки за время t, (путь S – в метрах, время t – в секундах). Производная от пути по времени, есть средняя скорость движения материальной точки: V(t) = S′(t)
Слайд 9Как вычислить силу тока, если известен закон изменения заряда по времени?
Пусть q = q(t) – заряд переносимый электрическим током через поперечное сечение проводника за время t, (заряд q - в кулонах, сила тока I - в амперах). Производная от заряда по времени есть сила тока:
I(t) = q′(t)
I(t) = q′(t)
Слайд 10Как вычислить мощность, если известен закон производимой работы по времени?
Пусть A
= A(t) – работа,
как функция времени,
(работа A - в джоулях, мощность N - в ваттах).
Производная от работы по времени,
есть мгновенная мощность
N(t) = A′(t)
как функция времени,
(работа A - в джоулях, мощность N - в ваттах).
Производная от работы по времени,
есть мгновенная мощность
N(t) = A′(t)
Слайд 11Задачи
Группа 1:
Движение материальной точки описывает закон
S(t) = 2 t3 – 5t2+ 3
1) Выведите формулу скорости движения материальной точки;
2) Найдите мгновенную скорость в момент времени t0 = 2
Группа 2:
Количество заряда, протекающего через проводник, начиная с момента времени t = 0 задается формулой q(t) = 4 t3 – 3t 2 +7.
1) Выведите формулу изменения силы тока;
2) Найдите силу тока в момент времени t0 = 3.
Группа 3:
Работа совершаемая аппаратом при погружении тела, начиная с момента времени t = 0 задается формулой A(t) = 3 t3 – 2t 2 + 5.
1) Выведите формулу мощности аппарата;
2) Вычислите мощность в момент времени t0 = 3
1) Выведите формулу скорости движения материальной точки;
2) Найдите мгновенную скорость в момент времени t0 = 2
Группа 2:
Количество заряда, протекающего через проводник, начиная с момента времени t = 0 задается формулой q(t) = 4 t3 – 3t 2 +7.
1) Выведите формулу изменения силы тока;
2) Найдите силу тока в момент времени t0 = 3.
Группа 3:
Работа совершаемая аппаратом при погружении тела, начиная с момента времени t = 0 задается формулой A(t) = 3 t3 – 2t 2 + 5.
1) Выведите формулу мощности аппарата;
2) Вычислите мощность в момент времени t0 = 3
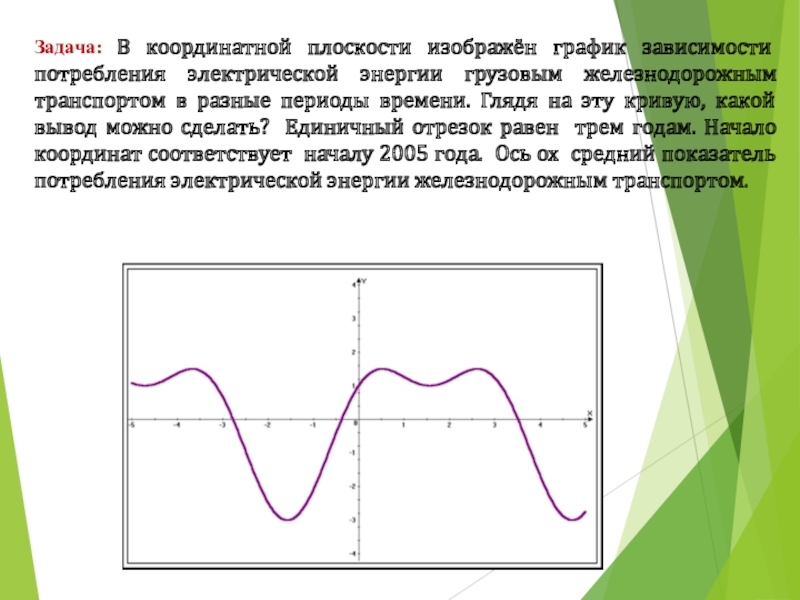
Слайд 12Задача: В координатной плоскости изображён график зависимости потребления электрической энергии грузовым
железнодорожным транспортом в разные периоды времени. Глядя на эту кривую, какой вывод можно сделать? Единичный отрезок равен трем годам. Начало координат соответствует началу 2005 года. Ось ох средний показатель потребления электрической энергии железнодорожным транспортом.
Слайд 14в чем состоит экономический смысл производной?
Если непрерывная функция y = f(x),
выражает зависимость объёма предоставляемых услуг y за единицу времени отраслью или предприятием, от объёма затраченного ресурса x – численности работников, то производная этой функции указывает на предельные издержки отрасли или предприятия за определённый период.
Слайд 15СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Найти область определения функции. (Указать множество значений переменной х, при
которых данная функция имеет значения).
Вычислить производную функции. (f ’(x))
Вычислить точки, в которых производная равна нулю. (Решить уравнение f ’(x) = 0 ).
На числовой прямой отметить точки, в которых производная равна нулю или не существует.
На каждом интервале определить знак производной. (f ’(x) > 0 или f ’(x) < 0)
В соответствии с признаками монотонности и экстремумов функции определить поведение функции на промежутках и характер критических точек. (Если f’(x)>0, то функция возрастает, если f’(x)<0, то функция убывает).
В соответствии с условием задачи записать ответ.
Вычислить производную функции. (f ’(x))
Вычислить точки, в которых производная равна нулю. (Решить уравнение f ’(x) = 0 ).
На числовой прямой отметить точки, в которых производная равна нулю или не существует.
На каждом интервале определить знак производной. (f ’(x) > 0 или f ’(x) < 0)
В соответствии с признаками монотонности и экстремумов функции определить поведение функции на промежутках и характер критических точек. (Если f’(x)>0, то функция возрастает, если f’(x)<0, то функция убывает).
В соответствии с условием задачи записать ответ.
Слайд 16УСТНЫЙ ОПРОС
Достаточный признак возрастания функции.
Достаточный признак убывания функции.
Какие точки области определения
функции являются критическими точками.
Необходимое условие экстремума (теорема Ферма).
Признак максимума функции (упрощенная формулировка признака).
Признак минимума функции (упрощенная формулировка признака).
Необходимое условие экстремума (теорема Ферма).
Признак максимума функции (упрощенная формулировка признака).
Признак минимума функции (упрощенная формулировка признака).
Слайд 17Достаточный признак возрастания функции
Если функция f(x) непрерывна на
отрезке [а;b] и имеет неотрицательную производную в каждой точке интервала (а;b),
т.е. f ′ (x) >0, то функция f(x) возрастает на промежутке [а;b].
т.е. f ′ (x) >0, то функция f(x) возрастает на промежутке [а;b].
Слайд 18Достаточный признак убывания функции
Если функция f(x) непрерывна на
отрезке [а;b] и имеет неположительную производную в каждой точке интервала (а;b),
т.е f ′ (x)˂0, то функция f (x) убывает на промежутке [а;b].
т.е f ′ (x)˂0, то функция f (x) убывает на промежутке [а;b].
Слайд 19Необходимое условие экстремума
(Теорема Ферма)
Если точка х0
является точкой экстремума функции f(x),
и в этой точке существует производная f ′ (x),
то она равна нулю: f ′ (x) = 0.
и в этой точке существует производная f ′ (x),
то она равна нулю: f ′ (x) = 0.
Слайд 20Признак максимума функции
Если в точке х0 производная меняет знак с плюса
на минус, то х0 – есть точка максимума.
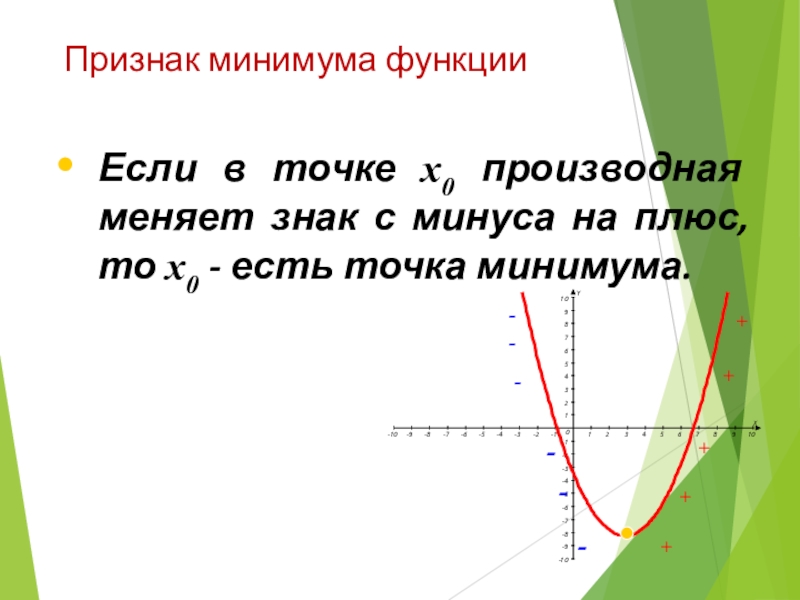
Слайд 21Признак минимума функции
Если в точке х0 производная меняет знак с минуса
на плюс, то х0 - есть точка минимума.
Слайд 22Исследовательская работа
Функция полных издержек локомотивного депо города N по перевозке грузов
имеет вид k(x) = x3 – 6x2 – 15x, где x – объём перевозок в условных единицах, выполненных предприятием. Определить при каком объёме перевозок средние издержки предприятия имели наименьшее значение. Ось Ох – средние издержки отрасли по перевозке грузов.
Слайд 23Оцените вашу работу на уроке
Продолжите фразу:
Урок для меня показался: интересным,
познавательным, неинтересным, ...
На уроке я работал: активно, пассивно, ...
Своей работой на уроке я: в целом доволен, недоволен, ...
За урок я смог : самостоятельно …, при помощи ...
Материал урока мне был: понятен, непонятен, ...
Мое настроение: улучшилось, ухудшилось,...
На уроке я работал: активно, пассивно, ...
Своей работой на уроке я: в целом доволен, недоволен, ...
За урок я смог : самостоятельно …, при помощи ...
Материал урока мне был: понятен, непонятен, ...
Мое настроение: улучшилось, ухудшилось,...
Слайд 24Исследуя функцию с помощью производной,
я Смог:
создать математическую модель заданной
ситуации;
находить область определения функции;
вычислять производную функции;
вычислять критические точки, определять их характер: выделять из них точки перегиба и точки экстремума;
определять поведение функции на числовых промежутках;
сформулировать ответ, в соответствии с задачей;
Готов к контрольной работе!!!
находить область определения функции;
вычислять производную функции;
вычислять критические точки, определять их характер: выделять из них точки перегиба и точки экстремума;
определять поведение функции на числовых промежутках;
сформулировать ответ, в соответствии с задачей;
Готов к контрольной работе!!!
Слайд 25ИТОГ УРОКА
Мы еще раз увидели взаимосвязь между свойствами функции и производной,
а также её применение в различных сферах.
Оценки за урок:
Оценки за урок:















![Презентация Производная и её применение Достаточный признак возрастания функции Если функция f(x) непрерывна на отрезке [а;b] Достаточный признак возрастания функции Если функция f(x) непрерывна на отрезке [а;b] и имеет неотрицательную производную](/img/thumbs/f38c2a17816c1d73c211461e64137df5-800x.jpg)
![Презентация Производная и её применение Достаточный признак убывания функции Если функция f(x) непрерывна на отрезке [а;b] Достаточный признак убывания функции Если функция f(x) непрерывна на отрезке [а;b] и имеет неположительную производную](/img/thumbs/ebde418b941c23a533d7f1c8b7624e7c-800x.jpg)