- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта на тему Функция, скрывающаяся за движением (9 класс)
Содержание
- 1. Презентация проекта на тему Функция, скрывающаяся за движением (9 класс)
- 2. Авторы проекта: Мерзляков Никита Координаторы проекта: учитель математики
- 3. Свободным падением называется движение тел под действием
- 4. 1 СЛУЧАЙ: ПАДЕНИЕ ВЕДРА В КОЛОДЕЦ
- 5. КАК ВЕДРО ПАДАЕТ В КОЛОДЕЦ?КАКИЕЗАКОНОМЕРНОСТИ ПРОЯВЛЯЮТСЯ В ПРОЦЕССЕ ПАДЕНИЯ? КАКОЙ ФУНКЦИЕЙМОЖНО ОПИСАТЬ ПАДЕНИЕ ВЕДРАМАТЕМАТИЧЕСКИ?
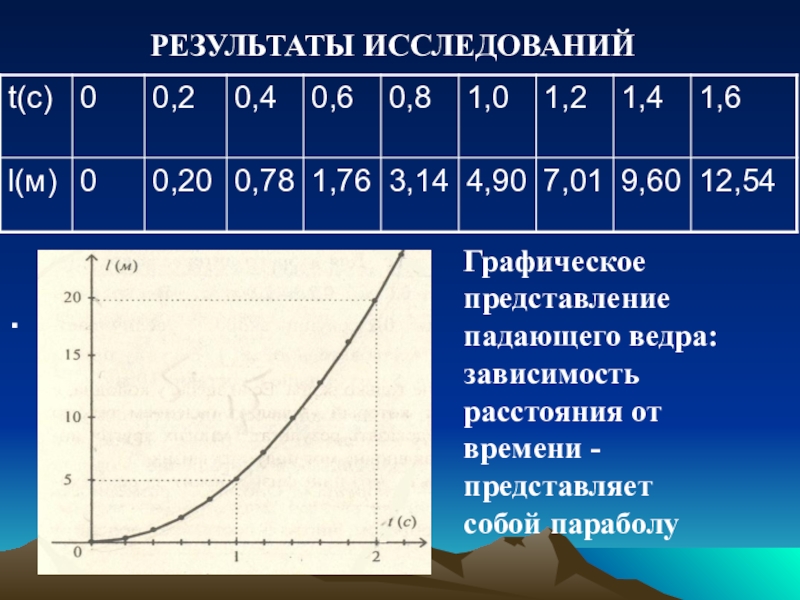
- 6. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ.Графическое представление падающего ведра: зависимость расстояния от времени -представляет собой параболу
- 7. Зависимость описывается функцией l(t) = ct²Чему равно
- 8. Что означает число 5?Найдем среднюю скорость на
- 9. Получаем, что за каждую секунду
- 10. Таким образом, в этом случае падения ведра
- 11. 2 СЛУЧАЙ ПАДЕНИЕ СОСУЛЬКИ h0 – высота
- 12. Таким образом, в случае падения сосульки с
- 13. 3 СЛУЧАЙ ПРЫЖОК ДЕЛЬФИНАДельфин участвует сразу
- 14. Слайд 14
- 15. 4 СЛУЧАЙ: ПОЛЕТ МЯЧА Единственное отличие данной
- 16. Таким образом, в случае полета мяча
- 17. Итак, во всех рассмотренных случаях свободного падения
- 18. Слайд 18
- 19. Мяч подбросили вертикально
- 20. Движение дельфина, выпрыгивающего из воды вертикально
- 21. Дельфин выпрыгивает из
- 22. Пусть h – высота (в
Авторы проекта: Мерзляков Никита Координаторы проекта: учитель математики и физики Кузьмина О.П. Образовательное учреждение: МОУ «Кулябинская ООШ»Учебный
Слайд 2Авторы проекта: Мерзляков Никита
Координаторы проекта: учитель математики и физики Кузьмина О.П.
Образовательное учреждение: МОУ «Кулябинская ООШ»
Учебный предмет: алгебра
Вид проекта: межпредметный, индивидуальный, среднесрочный,
информационный, практико- ориентированный.
Проблема: недостаточно знаний по использованию квадратичной функции при
описании физических процессов.
Цель проекта: рассмотреть использование квадратичной функции при описании
свободного падения тел.
Содержание проекта:
1. Использование квадратичной функции при описании свободного падения тел.
2. Задачи на использование квадратичной функции при описании свободного падения тел.
Форма презентации: информационный справочник, компьютерная презентация.
Результативность: информационный справочник, разработаны задачи по
использованию квадратичной функции при описании
свободного падения тел.
ПАСПОРТ ПРОЕКТА
Слайд 3Свободным падением называется движение тел под действием силы тяжести.
В жизни
свободное падение встречается часто: падение камня, полет мяча после того, как его ударит футболист, прыжок человека и др.
Рассмотрим 4 случая свободного падения тел:
1. Падение ведра в колодец.
2. Падение сосульки.
3. Прыжок дельфина.
4. Полёт мяча.
Слайд 5
КАК ВЕДРО ПАДАЕТ В
КОЛОДЕЦ?
КАКИЕ
ЗАКОНОМЕРНОСТИ
ПРОЯВЛЯЮТСЯ В
ПРОЦЕССЕ ПАДЕНИЯ?
КАКОЙ ФУНКЦИЕЙ
МОЖНО
ОПИСАТЬ
ПАДЕНИЕ ВЕДРА
МАТЕМАТИЧЕСКИ?
ПАДЕНИЕ ВЕДРА
МАТЕМАТИЧЕСКИ?
Слайд 6РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
.
Графическое представление
падающего ведра: зависимость расстояния от времени -представляет собой параболу
Слайд 7Зависимость описывается функцией
l(t) = ct²
Чему равно с?
Из первого измерения следует
0,2
= c х 0,22
c = 5
Результаты других измерений так же
показывают, что c = 5.
В итоге получаем, что c =5.
Значит, l(t) = 5t²
c = 5
Результаты других измерений так же
показывают, что c = 5.
В итоге получаем, что c =5.
Значит, l(t) = 5t²
Слайд 8
Что означает число 5?
Найдем среднюю скорость на каждом участке:
v1 = 0,2м
/0,2 с = 1 м/с.
v2 =(0,78 – 0,2)м /0,2с = 2,9 м/с.
v3 = 4,9 м/с и т.д.
Таким образом, за каждые 0,2 секунды скорость увеличивается примерно на 2 м/с, следовательно, за 1 секунду приращение скорости будет в 5 раз больше и составит 10 м/с.
Что
v2 =(0,78 – 0,2)м /0,2с = 2,9 м/с.
v3 = 4,9 м/с и т.д.
Таким образом, за каждые 0,2 секунды скорость увеличивается примерно на 2 м/с, следовательно, за 1 секунду приращение скорости будет в 5 раз больше и составит 10 м/с.
Что
Слайд 9 Получаем, что за каждую секунду скорость увеличивается на одну
и ту же величину – 10 м/с.
Такое движение называется равноускоренным, а приращение скорости за единицу времени – ускорением.
Оно имеет размерность (м/с)/с = м/с²
Число 5 составляет половину этого ускорения. И так, физик получает
l(t)= (g/2)t², где g= 10м/с²
Такое движение называется равноускоренным, а приращение скорости за единицу времени – ускорением.
Оно имеет размерность (м/с)/с = м/с²
Число 5 составляет половину этого ускорения. И так, физик получает
l(t)= (g/2)t², где g= 10м/с²
Слайд 10Таким образом, в этом случае падения ведра в колодец мы встретились
с квадратичной функцией вида:
y = aх²
Слайд 112 СЛУЧАЙ
ПАДЕНИЕ СОСУЛЬКИ
h0 – высота здания,
l – расстояние,
которое пролетела сосулька.
В момент времени t: h = hₒ – l.
Сосулька свободно падает, как и ведро в колодец. Следовательно, за t секунд она пролетит точно такое же расстояние, что и ведро:
l = (g/2) t².
Поэтому высота, на которой находится сосулька в момент времени t, равна
h = hₒ- (g/2) t².
В момент времени t: h = hₒ – l.
Сосулька свободно падает, как и ведро в колодец. Следовательно, за t секунд она пролетит точно такое же расстояние, что и ведро:
l = (g/2) t².
Поэтому высота, на которой находится сосулька в момент времени t, равна
h = hₒ- (g/2) t².
Слайд 12Таким образом, в случае падения сосульки с высоты получили квадратичную функцию
вида
у = aх² + b
у = aх² + b
Слайд 133 СЛУЧАЙ
ПРЫЖОК ДЕЛЬФИНА
Дельфин участвует сразу в двух движениях: равномерно летит
вверх и равноускоренно падает вниз.
В равномерном движении вверх дельфин за время t поднимается на высоту H = vₒ t.
При падении вниз, как сосулька или ведро, дельфин пролетает путь
l = (g/2)t²
В результате через t секунд он оказывается на высоте h = H –l.
Получаем формулу, описывающую изменение во времени высоты дельфина над водой
В равномерном движении вверх дельфин за время t поднимается на высоту H = vₒ t.
При падении вниз, как сосулька или ведро, дельфин пролетает путь
l = (g/2)t²
В результате через t секунд он оказывается на высоте h = H –l.
Получаем формулу, описывающую изменение во времени высоты дельфина над водой
h = vₒt – (g/2)t².
Слайд 154 СЛУЧАЙ: ПОЛЕТ МЯЧА
Единственное отличие данной ситуации от ситуации с
прыжком дельфина состоит в том, что полет мяча начинается не с нулевой высоты. Как и в случае с сосулькой, это отличие приводит к появлению в правой части формулы слагаемого h0.
h = hₒ + vₒt – (g/2)t²
h = hₒ + vₒt – (g/2)t²
Слайд 16Таким образом, в случае полета мяча с высоты получили квадратичную функцию вида: y
= aх² + aх + c
Слайд 17Итак, во всех рассмотренных случаях свободного падения тел мы встретились с квадратичной
функцией
y = aх² + bх + c
разного вида
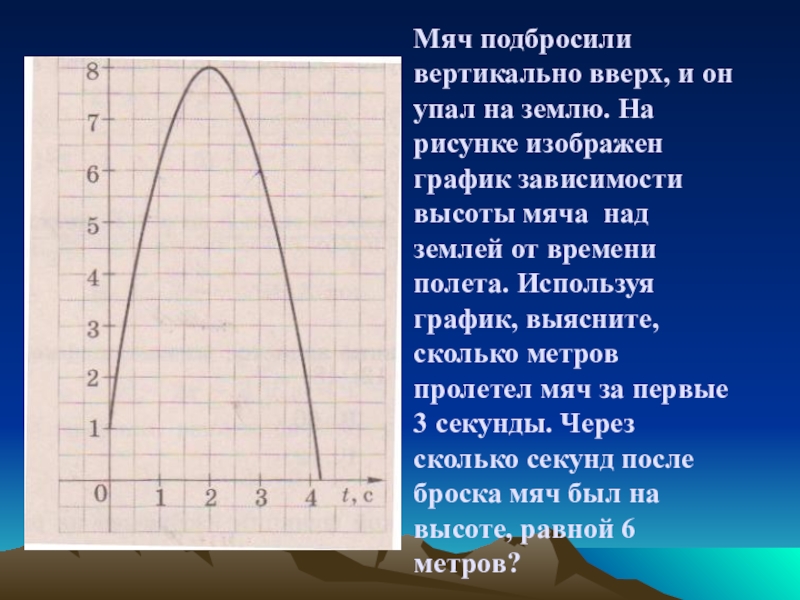
Слайд 19 Мяч подбросили вертикально вверх, и он упал на землю. На рисунке
изображен график зависимости высоты мяча над землей от времени полета. Используя график, выясните, сколько метров пролетел мяч за первые 3 секунды. Через сколько секунд после броска мяч был на высоте, равной 6 метров?
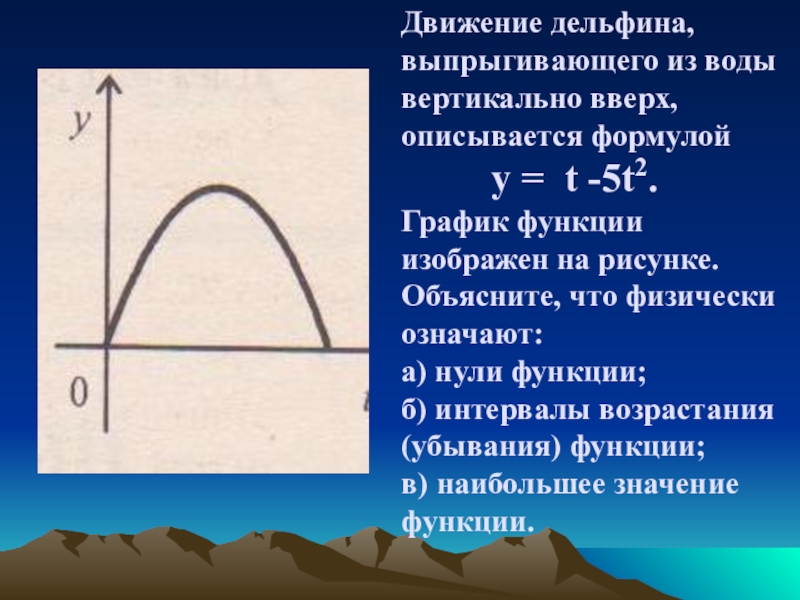
Слайд 20 Движение дельфина, выпрыгивающего из воды вертикально вверх, описывается формулой
у = t -5t2.
График функции изображен на рисунке. Объясните, что физически означают:
а) нули функции;
б) интервалы возрастания (убывания) функции;
в) наибольшее значение функции.
Слайд 21
Дельфин выпрыгивает из воды вертикально вверх со
скоростью v0=10 м/c.
Через сколько секунд он упадет в воду?
Через сколько секунд он упадет в воду?
Слайд 22 Пусть h – высота (в метрах), на которой находится
брошенный с земли вверх мяч,
t- время полета мяча ( в секундах). Зависимость h от t выражается формулой
h (t) = 24,5t – 4,9t²
Какой наибольшей высоты достиг мяч?
В какой промежуток времени он поднимался
и в какой опускался?
Через сколько секунд после броска он упал на
землю?
t- время полета мяча ( в секундах). Зависимость h от t выражается формулой
h (t) = 24,5t – 4,9t²
Какой наибольшей высоты достиг мяч?
В какой промежуток времени он поднимался
и в какой опускался?
Через сколько секунд после броска он упал на
землю?