школы не обучать приемам исчисления , а обучить приемам человеческой мысли при исчислении»
(Л.Н. Толстой)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Теория вероятностей
Содержание
- 1. Презентация по теме Теория вероятностей
- 2. Основные понятияИспытаниеСобытие Испытание- результат
- 3. Слайд 3
- 4. Полная группа событий Несколько событий образуют полную
- 5. Равновозможные события Равновозможные события – это
- 6. ВероятностьВероятность – это отношение числа благоприятных этому
- 7. Свойства
- 8. Основные формулы комбинаторики Комбинаторика - изучает
- 9. ПерестановкиПерестановки- комбинации, составленные из одних и тех
- 10. РазмещенияРазмещения – комбинации составленные из n
- 11. СочетанияСочетания- комбинации, составленные из элементов n по m элементов, которые отличаются хотя бы одним элементом.
- 12. Правило суммыЕсли некоторый объект А может
- 13. Правило умножения
- 14. Относительная частотаОтносительная частота предполагает, что были проведены
- 15. Слайд 15
- 16. Свойство геометрической вероятности
- 17. Суммой А + В двух событий
- 18. Сумма нескольких событий- событие, которое состоит в
- 19. Противоположные события Противоположными событиями
- 20. Умножение вероятностей.Произведением двух событий А и В
- 21. Условная вероятность
- 22. Умножение вероятностейВероятность совместного появления двух событий
- 23. .
- 24. Свойство
- 25. Независимые событияСобытие В называется независимым
- 26. Несколько событий называют попарно независимые, если каждые
- 27. Вероятность появления хотя бы 1 события
- 28. Сложение вероятностей совместных событийВероятность появления хотя бы
- 29. Формула полной вероятности
- 30. Формула Бейеса
- 31. Повторение испытаний
Основные понятияИспытаниеСобытие Испытание- результат (события). Событие случайное - если при определенных совокупностях условий оно может произойти или не произойти, если произведено испытание.
Слайд 2 Основные понятия
Испытание
Событие
Испытание- результат (события).
Событие случайное -
если при определенных совокупностях условий оно может произойти или не произойти, если произведено испытание.
Слайд 3
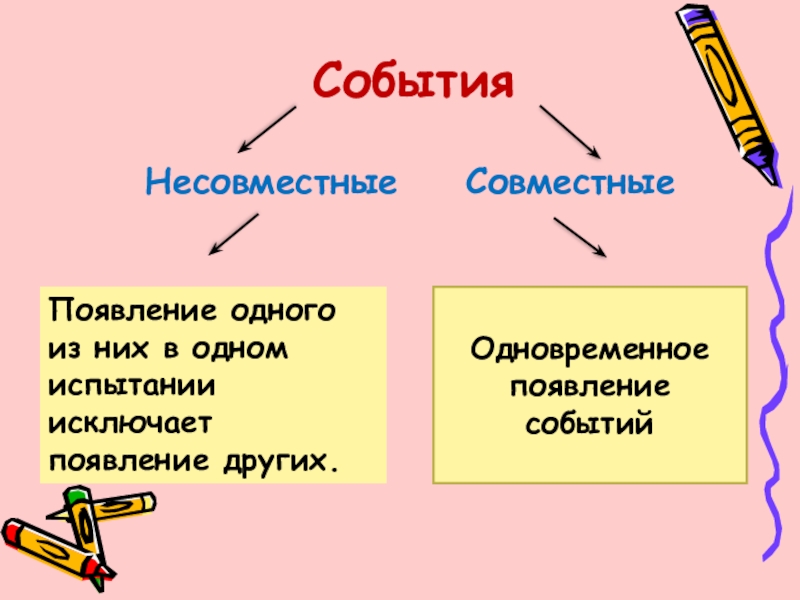
События
Несовместные Совместные
Появление одного из них в одном испытании исключает появление других.
Одновременное появление
событий
Слайд 4Полная группа событий
Несколько событий образуют полную группу событий, если в
результате испытания появится хотя бы одно из них.
Если события образующие полную группу, попарно несовместны, то в результате появится одно и только одно из этих событий.
Если события образующие полную группу, попарно несовместны, то в результате появится одно и только одно из этих событий.
Слайд 5Равновозможные события
Равновозможные события – это события, одно из которых
не является более возможным,
чем другие.
чем другие.
Слайд 6Вероятность
Вероятность – это отношение числа благоприятных этому событию исходов к общему
числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
( классическое)
( классическое)
Слайд 8Основные формулы комбинаторики
Комбинаторика - изучает
количество комбинаций,
подчиненных
определенным
условиям, которые можно
составить из элементов,
безразлично какой природы,
заданного конечного множества.
условиям, которые можно
составить из элементов,
безразлично какой природы,
заданного конечного множества.
Слайд 9Перестановки
Перестановки- комбинации, составленные из одних и тех же n элементов и
отличающиеся порядком их расположения.
Число перестановок различных n элементов
Число перестановок различных n элементов
Слайд 10Размещения
Размещения – комбинации составленные из n различных элементов по
m элементов, которые отличаются составом элементов либо их порядком.
Слайд 11Сочетания
Сочетания- комбинации, составленные из элементов n по m элементов, которые отличаются
хотя бы одним элементом.
Слайд 12
Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов
m способами, а объект В –
n способами, то выбрать либо А,
либо В можно m + n
способами.
n способами, то выбрать либо А,
либо В можно m + n
способами.
Слайд 14Относительная частота
Относительная частота предполагает, что были проведены испытания, а затем произведён
подсчёт вероятности.
При большом количестве повторений относительная частота имеет свойство устойчивости и колеблется около некоторого постоянного числа - вероятности появления события.
При большом количестве повторений относительная частота имеет свойство устойчивости и колеблется около некоторого постоянного числа - вероятности появления события.
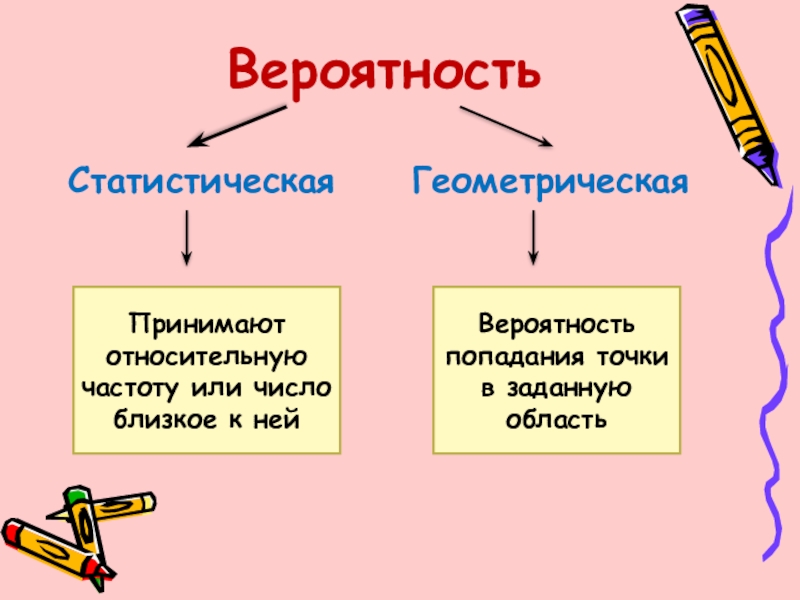
Слайд 15 Вероятность
Статистическая Геометрическая
Принимают относительную частоту или число близкое к ней
Вероятность попадания точки в заданную область
Слайд 17 Суммой А + В двух событий А и В
называют событие, состоящее в
появлении события А или В или двух
событий.
Если А и В несовместны, то А + В - появление любого из этих событий.
Р(А+В) = р(А) + р (В)
появлении события А или В или двух
событий.
Если А и В несовместны, то А + В - появление любого из этих событий.
Р(А+В) = р(А) + р (В)
Сложение вероятностей
Слайд 18
Сумма нескольких событий- событие, которое состоит в появлении хотя бы одного
из этих событий.
А+В+С-( А,В,С; А и В; А и С; В и С;
А и В и С)
Р(А+В+ С)= Р(А) + р(В) +р(С).
Р( А+В +…+Z) = р(А) + р(В) +… + р(Z)
А+В+С-( А,В,С; А и В; А и С; В и С;
А и В и С)
Р(А+В+ С)= Р(А) + р(В) +р(С).
Р( А+В +…+Z) = р(А) + р(В) +… + р(Z)
Слайд 19 Противоположные события
Противоположными событиями называют два единственно
возможных события, образующих полную группу А и не А. __
р(А) + р (А) = 1
p + q = 1
р(А) + р (А) = 1
p + q = 1
Слайд 20Умножение вероятностей.
Произведением двух событий А и В называют событие АВ состоящее
в совместном появлении этих событий.
Произведением нескольких событий называют событие, состоящее в появлении совместно всех этих событий.
Произведением нескольких событий называют событие, состоящее в появлении совместно всех этих событий.
Слайд 22 Умножение вероятностей
Вероятность совместного появления двух событий равна произведению вероятности
одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило.
р(АВ) = р(А)·р(В)
р(АВ) = р(А)·р(В)
Слайд 25
Независимые события
Событие В называется независимым
от события А, если появление
события А не изменяет вероятности
события В.
Два события независимы, если вероятность их совмещения равна произведению вероятностей этих событий.
Если А и В независимы, то независимы
_ _ _ _
А и В, А и В , А и В.
Слайд 26
Несколько событий называют попарно независимые, если каждые два из них независимы.
А,В
и С независимы , если
А и В, А и С , В и С независимы.
р(АВС) = р (А) р (В) р (С)
А и В, А и С , В и С независимы.
р(АВС) = р (А) р (В) р (С)
Слайд 28Сложение вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместных
событий:
- для независимых событий
- для зависимых событий