- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Решение текстовых задач ( подготовка к ГИА учащихся 9 класса)
Содержание
- 1. Презентация по теме Решение текстовых задач ( подготовка к ГИА учащихся 9 класса)
- 2. Умение решать задачи является одним из основных
- 3. Решить математическую задачу- это значит найти такую
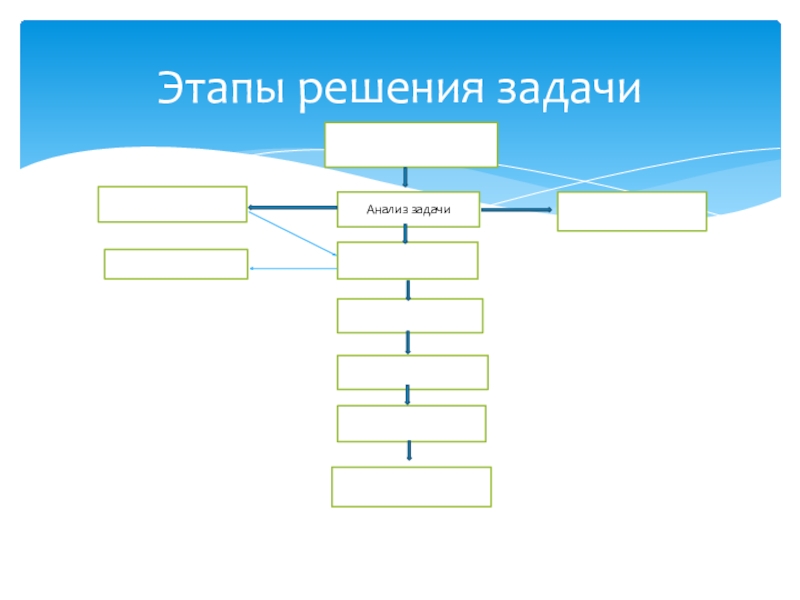
- 4. Этапы решения задачи
- 5. Все текстовые математические задачи по числу действий,
- 6. Умение решать простые задачи является подготовительной ступенью
- 7. Задачи на движение.Задачи на процентное содержание.
- 8. 1. Движение по суше
- 9. Два поезда вышли навстречу друг другу одновременно
- 10. Пусть Х-км/ч скорость одного поезда;Х+5- км/ч скорость
- 11. Лодка может проплыть 15км по течению реки
- 12. Задачи на работу содержат следующие величины:А- объем
- 13. 1) Объем выполненной работы известен, т.е. если
- 14. Один мастер может выполнить заказ за 12
- 15. Слайд 15
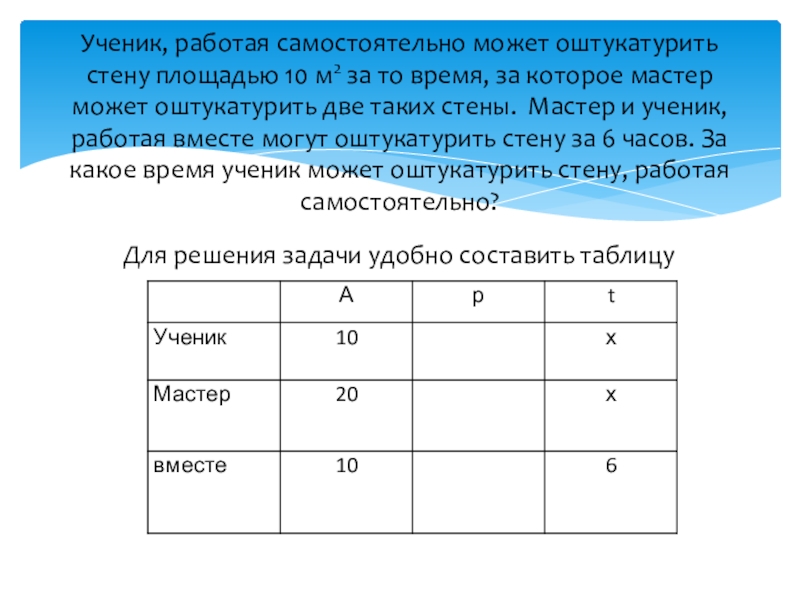
- 16. Для решения задачи удобно составить таблицуУченик, работая
- 17. Слайд 17
- 18. Три алгоритма:1). Нахождения части от целого;
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Пусть Хр. клиент внёс на 1-ый вклад,
- 23. Магазин обуви покупает туфли по оптовой цене
- 24. Новая цена составляет 124%. Получим: 372:1,24=300(р.) Ответ: 300р. Цена
- 25. Задачи на смеси и сплавыМ- масса
- 26. ДВА ВИДА ЗАДАЧ НА СМЕСИ
- 27. В траве содержалось 60% воды, значит, «сухого
- 28. Для удобства условие оформим в виде таблицы Сколько
- 29. m = 0,45 × 12 =
- 30. Сборник заданий для подготовки к государственной итоговой
- 31. Спасибо за внимание !
Слайд 1Решение
текстовых задач
при подготовке к ГИА
Манахова Елена Алексеевна
Учитель математики МОУ «ООШ №
Заводского района г. Саратова
Слайд 2Умение решать задачи является одним из основных показателей уровня математического развития,
При решении задач формируются различные математические понятия, осмысливаются различные арифметические операции.
Особенно важна роль задач как средства развития логического мышления учащихся, их умения устанавливать зависимости между величинами, делать правильные умозаключения.
Решая задачи , учащиеся приобретают новые математические знания, готовятся к практической деятельности.
Слайд 3Решить математическую задачу- это значит найти такую последовательность общих положений математики,
Слайд 5Все текстовые математические задачи по числу действий, выполняемых для их решения,
Задача, для решения которой надо выполнить один раз арифметическое действие, называется простой.
Задача, для решения которой надо выполнить несколько действий, связанных между собой (независимо от того, будут ли это разные или одинаковые действия), называется составной.
Слайд 6Умение решать простые задачи является подготовительной ступенью овладения учащимися умением решать
Решение составной задачи сводится к расчленению её на ряд простых задач и к последовательному их решению.
Слайд 7 Задачи на движение.
Задачи на процентное содержание.
Задачи на совместную
Задачи на концентрацию и сплавы.
Основные типы задач
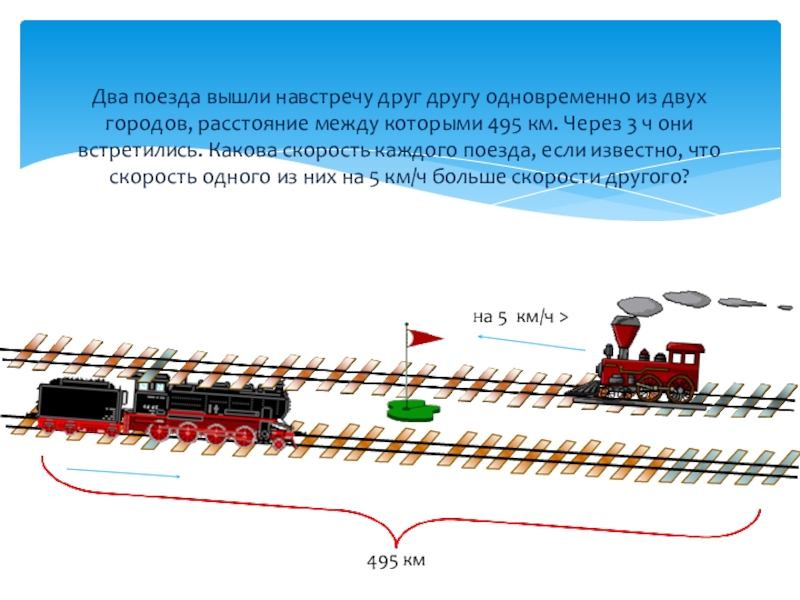
Слайд 9Два поезда вышли навстречу друг другу одновременно из двух городов, расстояние
на 5 км/ч >
495 км
Слайд 10Пусть Х-км/ч скорость одного поезда;
Х+5- км/ч скорость другого поезда;
(Х+ Х+5)- км/ч
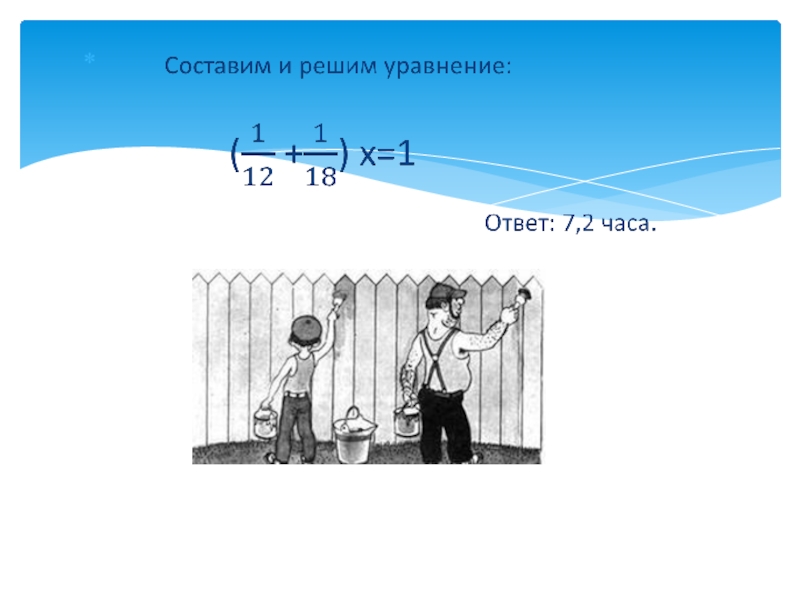
Составим и решим уравнение: (х+х+5)3=495.
Ответ: 80 км/ч, 85 км/ч.
Слайд 11 Лодка может проплыть 15км по течению реки и ещё 6км против
Слайд 12Задачи на работу содержат следующие величины:
А- объем выполненной работы
Р- производительность труда
t-
Уравнение, связывающее эти три величины, имеет вид: А= Рt
Задачи на совместную работу.
Слайд 131) Объем выполненной работы известен, т.е. если речь идет о количестве
2) Объем выполненной работы неизвестен, т.е. если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу.
Два случая при решении задач на совместную работу:
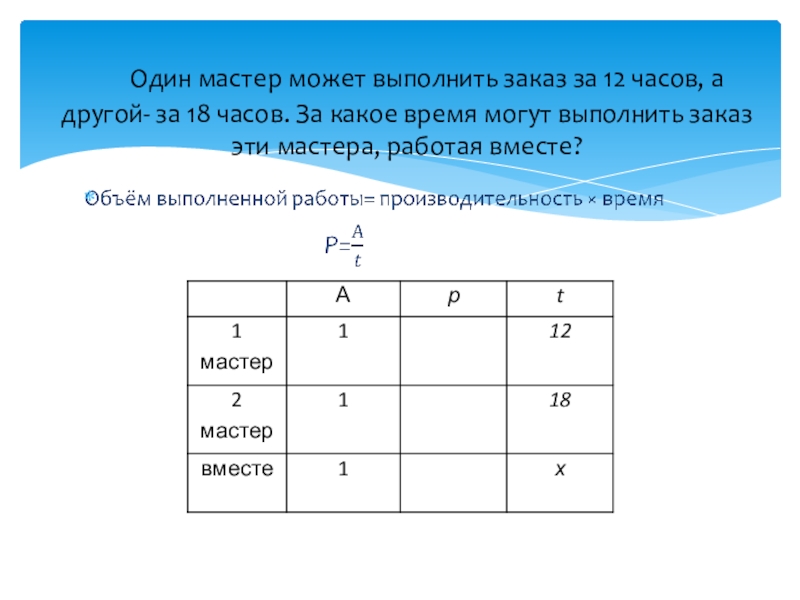
Слайд 14 Один мастер может выполнить заказ за 12 часов, а другой- за
Слайд 16 Для решения задачи удобно составить таблицу
Ученик, работая самостоятельно может оштукатурить стену
Слайд 18 Три алгоритма:
1). Нахождения части от целого;
2). восстановление целого по
3). нахождение процентного прироста.
Задачи на процентное содержание
Слайд 22Пусть Хр. клиент внёс на 1-ый вклад, тогда 3000-х р. клиент
0,08х р. годовой доход на 1-ый вклад;
0,1(3000-х) р. годовой доход на 2-ой вклад.
Доход на оба вклада составил 3260-3000= 260 р.
Составим и решим уравнение: 0,08х+0,1(3000-х)=260.
Ответ: 2000р., 1000р.
Клиент внес 3000 р. на два вклада, один из которых дает годовой доход, равный 8%, а другой- 10%. Через год на двух счетах у него было 3260 р. Какую сумму клиент внёс на каждый вклад?
Слайд 23 Магазин обуви покупает туфли по оптовой цене 750 рублей за пару,
Слайд 24
Новая цена составляет 124%. Получим: 372:1,24=300(р.)
Ответ: 300р.
Цена товара была повышена на
Слайд 25 Задачи на смеси и сплавы
М- масса смеси
m- масса вещества
c=m/M -
с×100%- процентное содержание данного вещества
m=c×M- масса данного вещества в смеси (сплаве)
Слайд 27В траве содержалось 60% воды, значит, «сухого вещества» было 40%. В
80% от х= 40% от 1000
Составим уравнение:
0,8х= 0,4× 1000
Х=500 (кг)
Ответ: 500 кг.
Влажность свежескошенной травы 60%, сена- 20%. Сколько сена получится из 1т свежескошенной травы?
Слайд 28
Для удобства условие оформим в виде таблицы
Сколько граммов 75%-ного раствора кислоты
Составим уравнение и решим его:
(4,5+0,75х)/(х+30) ×100%= 50%.
Х=42 г Ответ: 42 г .
Слайд 29 m = 0,45 × 12 = 5,4 кг (где 0,45
Пусть x кг олова надо добавить к сплаву. Тогда 12+х кг – масса нового сплава. И так как масса меди в первоначальном сплаве равна 5,4 кг, то имеем пропорцию:
12 + x - 100%
5,4 - 40%
Составим уравнение: 40 (12 + х ) = 100 · 5,4
решая его, получаем х=1,5 кг.
Ответ: нужно добавить 1,5 кг чистого олова.
Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Слайд 30Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе
Математика. Итоговая аттестация 2013, под ред. Д.А.Мальцева, «Народное образование» , 2013г.
Как научиться решать задачи, Л.М.Фридман, Е.Н.Турецкий, Москва, «Просвещение», 1979 г.
Справочник по методам решения задач по математике, А.И.Пинский, А.Г.Цыпкин, Москва, «Наука», 1989г.
Математика. Тематические тренировочные задания. В.В.Кочагин, М.Н.Кочагина, Москва, «Эксмо», 2012г.
Используемая литература.