- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Решение показательных и логарифмических неравенств (11 класс)
Содержание
- 1. Презентация по теме: Решение показательных и логарифмических неравенств (11 класс)
- 2. Метод рационализации позволяет перейти от неравенства содержащего
- 3. Таблица работает при условии :f›0,g›0,h›0,h≠1где f
- 4. И еще несколько полезных следствий :где f и
- 5. Пример 1:
- 6. Слайд 6
- 7. Пример 2:
- 8. Слайд 8
- 9. Задание для решения с доской: Ответ:(0;0,5) U [2;3]
- 10. Рассмотрим таблицы, позволяющие рационализировать показательный неравенства .
- 11. Пример: (x2-x-2)2x-6 ≥ (x2-x-2)3-4x X2-x-2›0 х2-x-2
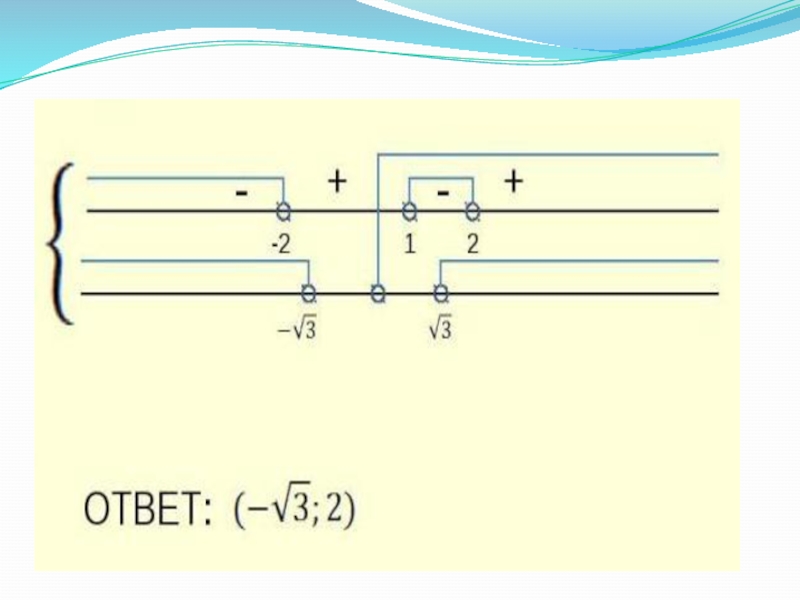
- 12. Упорядочим корни:Так как 3‹ √13 ‹4,то
- 13. Устное упражнение: назвать чему равносильно данное неравенство
- 14. Решение.1.Решим первое неравенство:2. Решим второе неравенство
- 15. Так как
Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные выражения к равносильному ему рациональному неравенству.Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности
Слайд 2Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные
выражения к равносильному ему рациональному неравенству.
Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)
Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)
Слайд 3
Таблица работает при условии :f›0,g›0,h›0,h≠1
где f и g— функции от х,
h— функция
или число,
V— один из знаков ≤,›,≥,‹
Заметим также, вторая и третья строчки таблицы — следствия первой.
V— один из знаков ≤,›,≥,‹
Заметим также, вторая и третья строчки таблицы — следствия первой.
Метод рационализации в логарифмических неравенствах
Слайд 4И еще несколько полезных следствий :
где f и g — функции от
x,
h— функция или число,
V— один из знаков ‹,≥,≤,›
h— функция или число,
V— один из знаков ‹,≥,≤,›
Слайд 10Рассмотрим таблицы, позволяющие рационализировать показательный неравенства .
Таблица для рационализации в
показательных неравенствах:
f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии h›0,h≠1.
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.
f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии h›0,h≠1.
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.
Слайд 11Пример:
(x2-x-2)2x-6 ≥ (x2-x-2)3-4x
X2-x-2›0
х2-x-2 ≠1
((X2-x-2)-1)((2x-6)-(3-4x))≥ 0
x›2
x‹-1
(x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5
x‹-1
(x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5
,
Слайд 13Устное упражнение: назвать чему равносильно данное неравенство без учёта ОДЗ
1.logx-3(x2+3x-4)≤ logx-3(5-x)
2.(x-3)x-4
≤
Далее рассмотрим пример решения системы неравенств:
Далее рассмотрим пример решения системы неравенств:
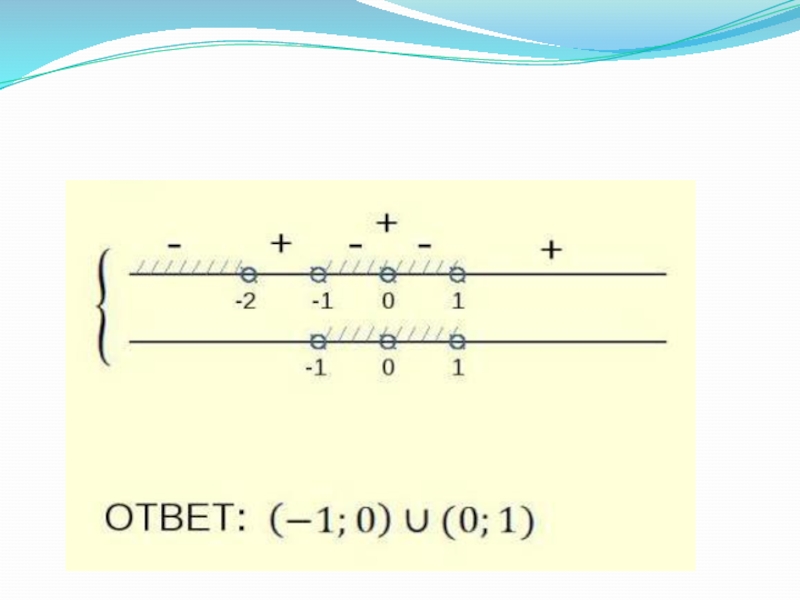
Слайд 14Решение.
1.Решим первое неравенство:
2. Решим второе неравенство
при всех х
При условиях и получаем неравенство
При указанных условиях получаем:
3. Решением системы является общая часть решений двух неравенств.
При условиях и получаем неравенство
При указанных условиях получаем:
3. Решением системы является общая часть решений двух неравенств.






![Презентация по теме: Решение показательных и логарифмических неравенств (11 класс) Задание для решения с доской: Ответ:(0;0,5) U [2;3] Задание для решения с доской: Ответ:(0;0,5) U [2;3]](/img/thumbs/81e9f7f080b7927ec777732fd8ab5b9d-800x.jpg)