- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Понятие логарифма
Содержание
- 1. Презентация по теме: Понятие логарифма
- 2. Понятие логарифма.Логарифмом положительного числа b по основанию
- 3. Примерыlog2 8 =log3 729 =log0,2 25 =log4
- 4. Сведения из истории.Потребность в сложных расчётах в
- 5. В 1614 году шотландский математик-любитель Джон Непер
- 6. Сведения из историиЛогарифмы необычайно быстро вошли в
- 7. Основные свойства логарифмов
- 8. Слайд 8
- 9. Понятие логарифмической функции.Функцию вида y = logaх,
- 10. График логарифмической функции y = logах,
- 11. а) При а > 1 функция возрастает
- 12. Уравнение, содержащее неизвестное под знаком логарифма или
- 13. Методы решения логарифмических уравненийИспользование определения логарифмаlogab =
- 14. Методы решения логарифмических уравненийИспользование свойств логарифмов Пример.
- 15. Методы решения логарифмических уравненийМетод подстановки Пример.
- 16. Логарифмические неравенстваНеравенства вида loga f(x) > logа
- 17. Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4].
- 18. Пример 3Пример 4Логарифмические неравенства. ПримерыОтвет: (0; 5) ∪ (40; 45).
Слайд 2Понятие логарифма
.
Логарифмом положительного числа b по основанию а называют показатель степени,
logab = c
ac = b (а ≠ 1, a > 0, b > 0)
- основное логарифмическое тождество
Слайд 3Примеры
log2 8 =
log3 729 =
log0,2 25 =
log4 8 =
log2 2 =
log10
log49 1/7 =
log0,1 10000 =
3, 23 = 8;
6, 36 = 729;
-2, (0,2)-2 = 25;
1,5, 41,5 = 8;
1, 21 = 2;
0, 100 = 1;
-0,5, 49-0,5 = 1/7;
-4, 0,1-4 = 10000.
Слайд 4Сведения из истории
.
Потребность в сложных расчётах в XVI веке быстро росла,
геометрической и арифметической прогрессии. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
Слайд 5В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке
Сведения из истории
Слово логарифм происходит от греческого λόγοφ (число) и αρινμοφ (отношение) и переводится, следовательно, как отношение чисел.
Слайд 6Сведения из истории
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не
Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером (1550 - 1617) и швейцарцем И. Бюрги (1552 - 1632).
Слайд 9Понятие логарифмической функции
.
Функцию вида
y = logaх, где а ≠ 1,
называют
логарифмической функцией
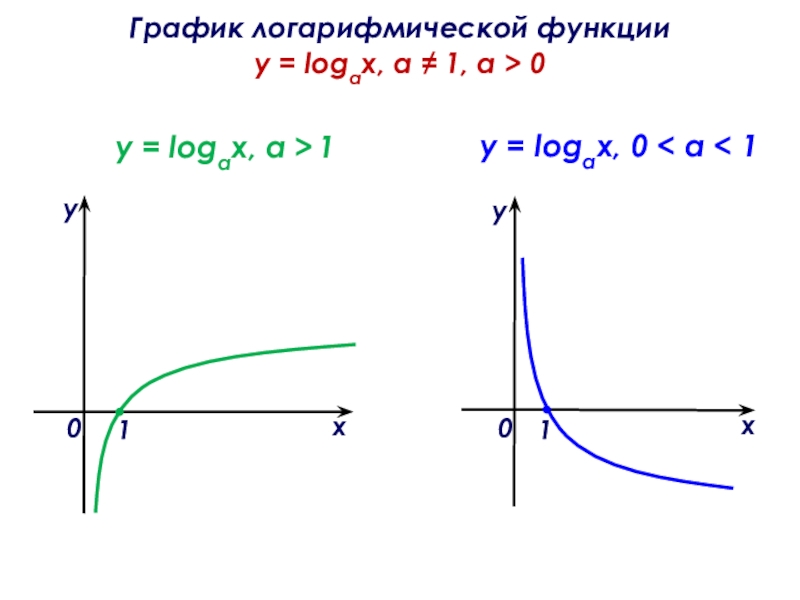
Слайд 10График логарифмической функции y = logах, а ≠ 1, a >
х
у
0
y = logaх, а > 1
1
y = logах, 0 < а < 1
х
у
0
1
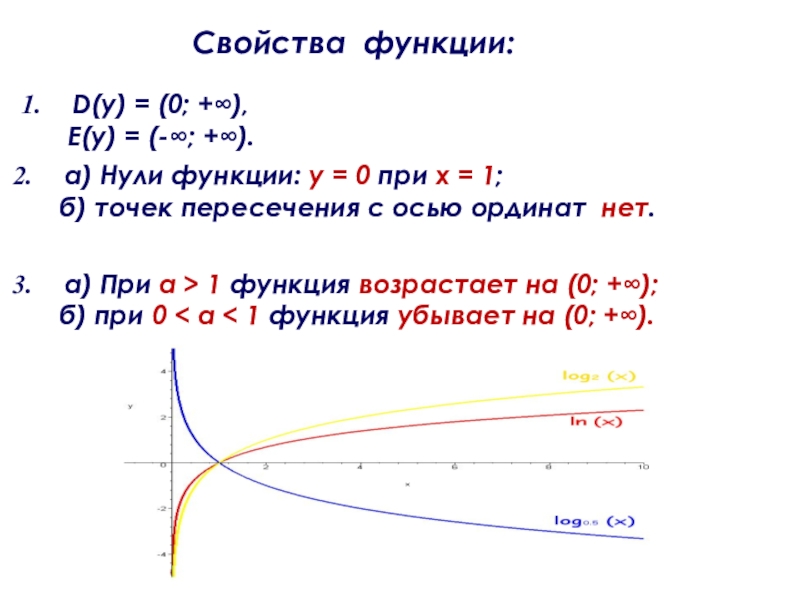
Слайд 11а) При а > 1 функция возрастает на (0; +∞);
б) при
а) Нули функции: у = 0 при х = 1;
б) точек пересечения с осью ординат нет.
Свойства функции:
D(y) = (0; +∞),
E(y) = (-∞; +∞).
Слайд 12Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании,
Логарифмические уравнения
Решение: x=ab ОДЗ не надо !
2) Сводящиеся к простейшим: loga f(x) = loga h(х)
⟺
Слайд 13Методы решения логарифмических уравнений
Использование определения логарифма
logab = c
Пример:
log2(5 + 3log2(x - 3)) = 3
Решение:
5+3log2(x-3) = 23
3log2(x-3) = 8-5 | :3
log2(x - 3) = 1
x - 3 = 21
x = 5
Ответ: 5
Слайд 14Методы решения логарифмических уравнений
Использование свойств логарифмов
Пример.
log3x + log3(x
Решение:
О.Д.З.: x>0,
х+3˃0,
х+24˃0
log3 (х(x + 3)) = log3(x + 24)
x(x+3)=x+24 ;
x2 + 2x - 24 = 0
x={-6;4} х = -6 -п.к. Ответ: x=4
Слайд 15Методы решения логарифмических уравнений
Метод подстановки
Пример.
lg2x - 3lgx +
Решение:
lg x = t lgx=1
t2-3t+2=0 lgx=2 x={10;100}
t =1, t = 2
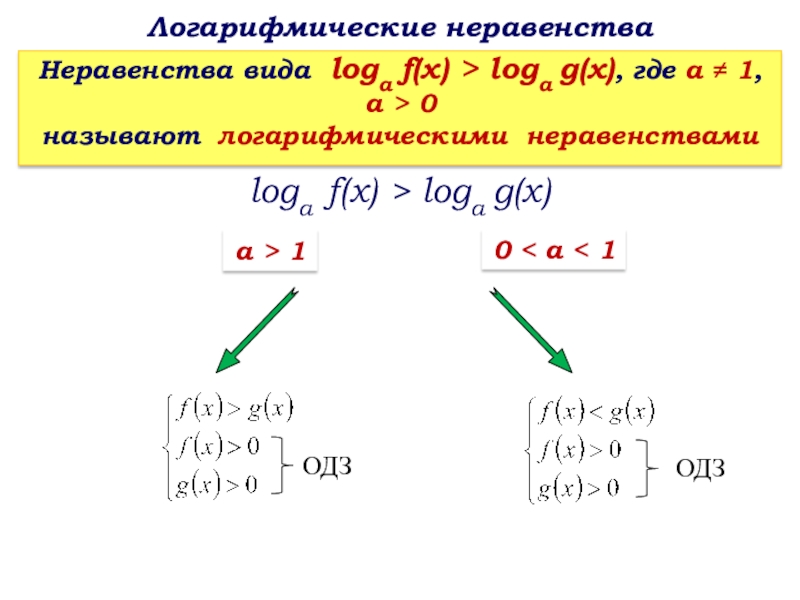
Слайд 16Логарифмические неравенства
Неравенства вида loga f(x) > logа g(х), где а ≠
называют логарифмическими неравенствами
loga f(x) > logа g(х)
0 < а < 1
а > 1
ОДЗ
ОДЗ












![Презентация по теме: Понятие логарифма Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4]. Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4].](/img/thumbs/1668c25a356bea57b8f8778e36e2da1d-800x.jpg)






