Производная
функции
11 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Определение производной
Содержание
- 1. Презентация по теме Определение производной
- 2. Пусть точка движется вдоль прямой по закону
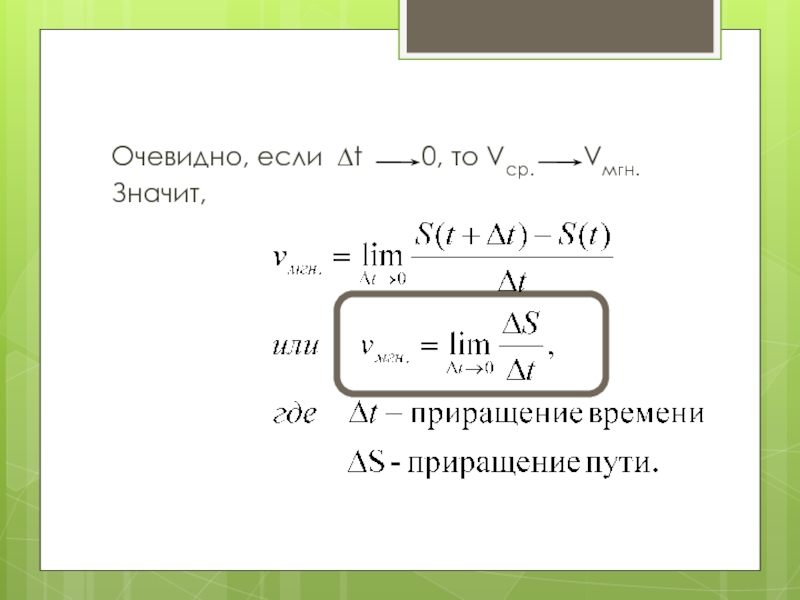
- 3. Очевидно, если ∆t 0, то Vср. Vмгн.Значит,
- 4. =x0+∆xПриращение функции и приращение аргументаy=f(x)x0f(x)=f(x0+∆x)f(x0)∆x∆fприращение аргумента:xy∆х =
- 5. Задача: Определить положение касательной (tgφ)ху0М0х0f(x0)Мхf(x)=x0+∆x∆x∆f=f(x0+∆x)αφСекущая, поворачиваясь вокруг
- 6. В математике операция нахождения предела отношения приращения
- 7. ОпределениеПроизводной функции называется предел отношения приращения функции
- 8. Физический смысл производной Механический смысл производной состоит
- 9. Геометрический смысл производной.Производная функции в точке x0
- 10. Схема вычисления производной функции1. Найти приращение функции
- 11. Пример: Вычислить производную функции y=x2Решение: Используем схему вычисления производной по действиям:1.2.3.
- 12. Задание: Найти производную функции:1.2.3.4.5.6.Решение 1Решение 3Решение 2Решение 4Решение 5Решение 6
- 13. Слайд 13
- 14. Домашнее задание1.2.
- 15. Решение 1: Вычислить производную функции Задания1.2.3.
- 16. Решение 2: Вычислить производную функции Задания1.2.3.
- 17. Решение 3: Вычислить производную функции Задания1.2.3.
- 18. Решение 4: Вычислить производную функции Задания1.2.3.
- 19. Решение 5: Вычислить производную функции Задания1.2.3.
- 20. Решение 6: Вычислить производную функции Задания1.2.3.
Пусть точка движется вдоль прямой по закону S(t).Тогда за промежуток времени t точка проходит расстояние S(t).Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).Тогда средняя скорость
Слайд 2
Пусть точка движется вдоль прямой по закону S(t).
Тогда за промежуток времени
t точка проходит расстояние S(t).
Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость
Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость
Слайд 4
=x0+∆x
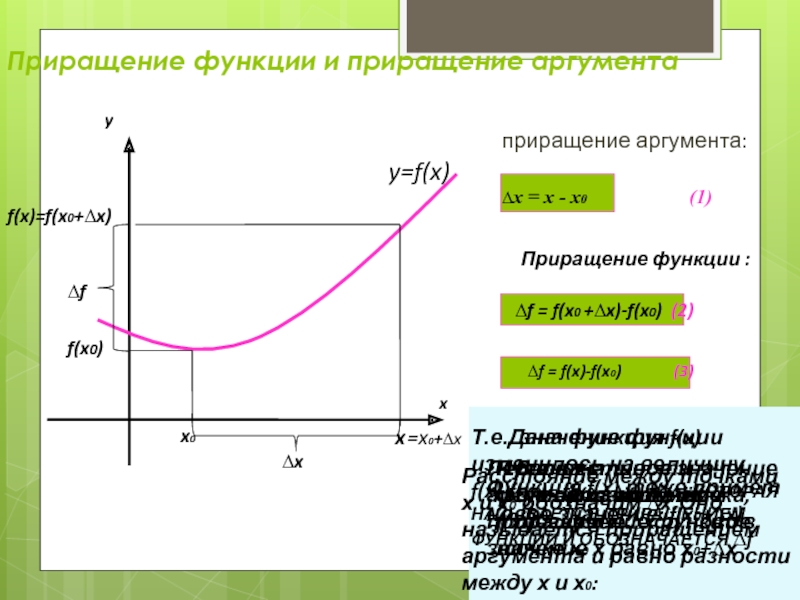
Приращение функции и приращение аргумента
y=f(x)
x0
f(x)=f(x0+∆x)
f(x0)
∆x
∆f
приращение аргумента:
x
y
∆х = х - х0
(1)
Приращение функции :
∆f = f(x0 +∆x)-f(x0) (2)
∆f = f(x)-f(x0) (3)
x
В окрестности точки х0 возьмём точку х
Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0
Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:
Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х
Функция f(х) тоже примет новое значение: f(x0+∆x)
Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f
Дана функция f(x)
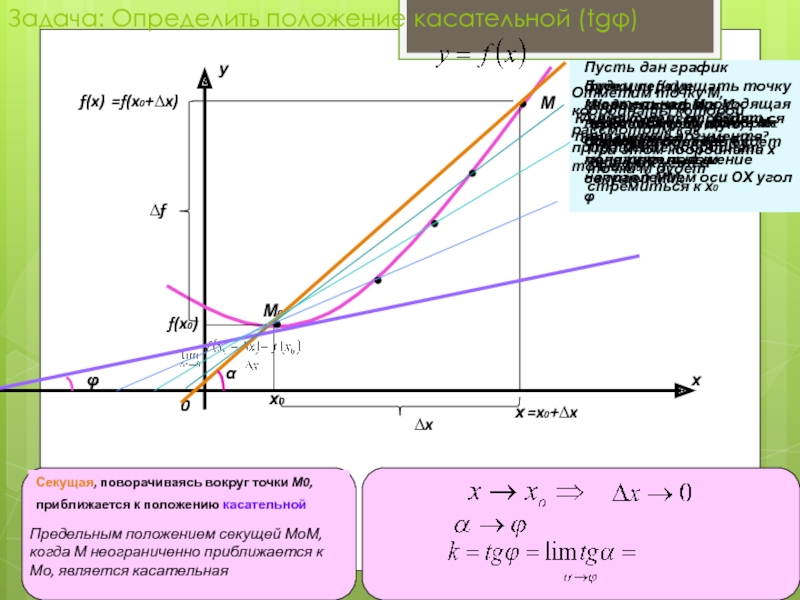
Слайд 5Задача: Определить положение касательной (tgφ)
х
у
0
М0
х0
f(x0)
М
х
f(x)
=x0+∆x
∆x
∆f
=f(x0+∆x)
α
φ
Секущая, поворачиваясь вокруг точки М0,
приближается к
положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается к Мо, является касательная
Пусть дан график функции f(х) и касательная, проходящая через точку М0 ,которая образует с положительным направлением оси ОХ угол φ
Отметим точку М, координаты которой рассмотрим как приращение координат точки М0
Через точки М и М0 проведём секущую, которая образует с осью ОХ угол α
Будем перемещать точку М вдоль графика, приближая её к точке М0.Соответственно будет меняться положение секущей ММ0
При этом координата х точки М будет стремиться к х0
К чему будет стремиться приращение аргумента?
А к какому углу будет стремиться угол α ?
Слайд 6В математике операция нахождения предела отношения приращения функции Δ f к
приращению аргумента Δ x , при условии, что приращение Δ x → 0 называется -
дифференцирование функции
Результат выполнения называют
производной
и обозначают:
Слайд 7Определение
Производной функции называется предел отношения приращения функции к приращению аргумента, когда
приращение аргумента стремится к нулю.
Обозначение или
Слайд 8
Физический смысл производной
Механический смысл производной состоит в том, что производная
пути по времени равна мгновенной скорости в момент времени t0:
S'(t)= Vмг(t)
S'(t)= Vмг(t)
Слайд 9Геометрический смысл производной.
Производная функции в точке x0 равна угловому коэффициенту касательной
к графику функции y = f(x) в этой точке.
Слайд 10Схема вычисления производной функции
1. Найти приращение функции на отрезке [ x;
x+Δx]:
2. Разделить приращение функции на приращение аргумента:
3. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
2. Разделить приращение функции на приращение аргумента:
3. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
![Схема вычисления производной функции1. Найти приращение функции на отрезке [ x; x+Δx]:2. Разделить приращение функции на приращение](/img/thumbs/f1345f567c6ff93425f8aaaa62d2ef05-800x.jpg "Презентация по теме Определение производной Схема вычисления производной функции1. Найти приращение функции на отрезке [ x;")
Слайд 11Пример: Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
1.
2.
3.
Слайд 12Задание: Найти производную функции:
1.
2.
3.
4.
5.
6.
Решение 1
Решение 3
Решение 2
Решение 4
Решение 5
Решение 6
