№9 г. Ульяновска
Овечкина Елена Викторовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Логарифмические уравнения (11 класс)
Содержание
- 1. Презентация по теме Логарифмические уравнения (11 класс)
- 2. «Если не верить в себя, нельзя быть
- 3. Логарифмический тренажер
- 4. Историческая справкаВ 1614 году шотландский математик-любитель Джон Непер ( 1550-1617) вошел
- 5. Историческая справкаОдновременно с Дж. Непером над составлением
- 6. Историческая справкаВ 1623 году, через 9 лет
- 7. Уравнение, содержащее переменную под знаком логарифма, называется
- 8. Методы решения логарифмических уравненийПо определению логарифма.На основе
- 9. 2. Метод потенцирования.Под потенцированием понимается переход от
- 10. 13. Метод введения новой переменнойlog22x – 4log2
- 11. 4. Метод логарифмированияx0,5lgx=0,01x2 Прологарифмируем обе части уравнения
- 12. 5. Метод приведения логарифмов к одному и
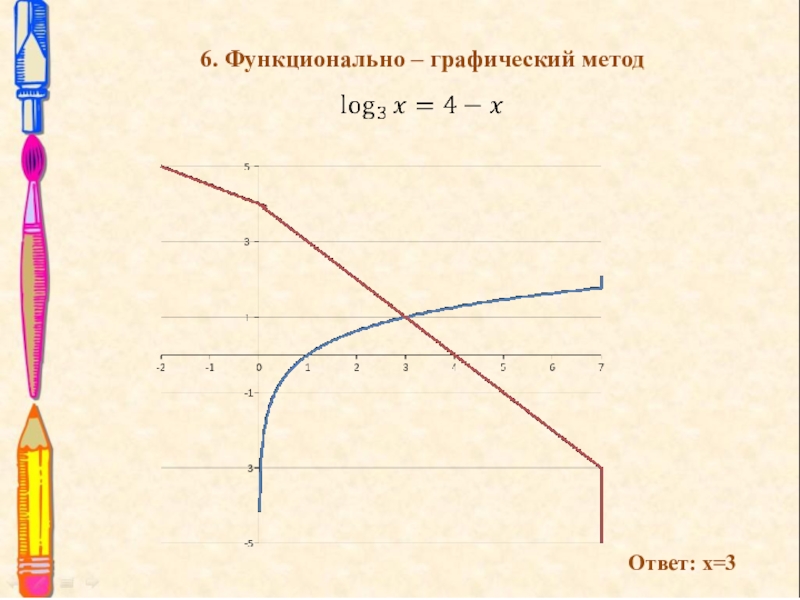
- 13. 6. Функционально – графический методОтвет: х=3
- 14. 7. Использование свойств монотонности функции log3 x
- 15. 8. Метод оценки Если f(x) ≦ m
- 16. Самостоятельная работа (в парах)Укажите метод и решите уравнения:Ответы (самопроверка)150,25; 162; -40, 125; 25125; 0,04-43; 27
- 17. Список использованной литературы : Мордкович А. Г.
«Если не верить в себя, нельзя быть гением» Оноре де Бальзак
Слайд 1Обобщающий урок
«Решение логарифмических уравнений»
11 класс
Учитель математики высшей квалификационной категории МБОУ СОШ
Слайд 4Историческая справка
В 1614 году шотландский математик-любитель Джон Непер ( 1550-1617) вошел в историю математики как
основатель термина «логарифм». Теорию логарифмов Дж. Непер изложил в книге «Описание удивительной таблицы логарифмов». техникой логарифмирования Непер владел уже к 1594 году. Непосредственной целью её разработки было облегчить Дж. Неперу сложные астрологические расчёты.
Слайд 5Историческая справка
Одновременно с Дж. Непером над составлением таблиц логарифмов работал швейцарский
ученый И. Бюрги (1552 – 1632). Он подготовил свои таблицы логарифмов чисел к 1610г., однако, они вышли в свет лишь в 1620г., уже после издания таблиц Дж. Непера, в следствие чего остались незамеченными.
Слайд 6Историческая справка
В 1623 году, через 9 лет после создания первых таблиц,
англ. математик Эдмунд Гантер изобрел первую логарифмическую линейку, ставшую рабочим инструментом для многих поколений.
Слайд 7Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим
Алгоритм решения логарифмического уравнения
Решить
уравнения, выбрав метод решения.
Проверить получение корня, подставив их в исходное уравнение
Проверить получение корня, подставив их в исходное уравнение
Найти область допустимых значений (ОДЗ) переменной.
Решить уравнение, выбрав метод решения
Выяснить, удовлетворяют ли корни уравнения ОДЗ
Слайд 8Методы решения логарифмических уравнений
По определению логарифма.
На основе определения логарифма решаются уравнения,
в которых по данным основанию и числу определяются логарифм, по данному логарифму и основанию определяется число и по данному числу и логарифму определяется основание.
X=2,5
Слайд 92. Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего логарифмы к
равенству, не содержащего их.
f(x) = y(x)
Условия для проверки всегда составляем по исходящему уравнению !
при
Слайд 101
3. Метод введения новой переменной
log22x – 4log2 x + 3=0
log2 x=
t, x>0
t2 – 4t + 3=0
t1=3 t2=1
log2 x=1 log2 x=3
x=2
x=8
Ответ: x=2; 8
Слайд 114. Метод логарифмирования
x0,5lgx=0,01x2
Прологарифмируем обе части уравнения по основанию 10
lg x
0,5lgx=lg 0,01x2
0,5 lg2x – 2lg x + 2 = 0
t2 – 4t + 4 = 0
t=lg x
0,5t2 – 2t - 2 = 0
(t-2)2 = 0
t = 2 lg x = 2
Ответ: x=100
Слайд 125. Метод приведения логарифмов к одному и тому же основанию
log9 (37
– 12x) * log7-2x 3 = 1
ОДЗ
0,5log3 (37 - 12x) = log3 (7 – 2x)
log3 (37 - 12x) = log3 (7 – 2x)2
37 – 12x = (7 – 2x)2
37 – 12x = 49 -28x + 4x2
X2 – 4x + 3 = 0
x1 = 1
x2 = 3 – посторонний корень
Ответ: х = 1
Слайд 147. Использование свойств монотонности функции
log3 x = 11 – x
Так
как функции y = log3 x возрастает, а у = 11 – x убывает на (0;+∞),
то уравнение имеет единственное решение, которое можно найти методом подбора: х = 9
то уравнение имеет единственное решение, которое можно найти методом подбора: х = 9
Слайд 158. Метод оценки
Если f(x) ≦ m , a g(x) ≧
m, равенство f(x) = g(x) возможно тогда и только тогда, когда f(x) и g(x) одновременно равны m
Решаем 1 уравнение системы и получаем корень. Подставляем в другое равнение:
log25 (x+1) ≥ 0;
Ответ: x = 0
Слайд 16Самостоятельная работа (в парах)
Укажите метод и решите уравнения:
Ответы (самопроверка)
15
0,25; 16
2; -4
0,
125; 2
5
125; 0,04
-4
3; 27
Слайд 17Список использованной литературы :
Мордкович А. Г. Алгебра и начала математического
анализа. 10—11 классы. В 2 ч.( Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. — 10-е изд., стер. — М. : 2013. — 399 с. : ил. ISBN 978-5-346-01136-1, ч. 2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Г. Мишустина, П. В. Семенов, Е. Е. Тульчинская ] ; под ред. А. Г. Мордковича. — 10-е изд., стер. — М. : 2013. — 239 с. : ил. ISBN 978-5-346-01137-8 )
Интернет ресурс :
http://images.yandex.ru/
