- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Квадратные уравнения
Содержание
- 1. Презентация по теме Квадратные уравнения
- 2. Девиз урокаСтремиться буду я решать уравнения на 5!
- 3. Является ли данное уравнение квадратным?Квадратные уравненияДаНет
- 4. Является ли данное уравнение квадратным?Квадратные уравненияДаНет
- 5. Квадратные уравненияДаНетЯвляется ли данное уравнение квадратным?
- 6. Квадратные уравненияДаНетЯвляется ли данное уравнение квадратным?
- 7. Квадратные уравненияДаНетЯвляется ли данное уравнение квадратным?
- 8. Квадратные уравненияДаНетЯвляется ли данное уравнение квадратным?
- 9. Квадратные уравненияДаНетЯвляется ли данное уравнение квадратным?
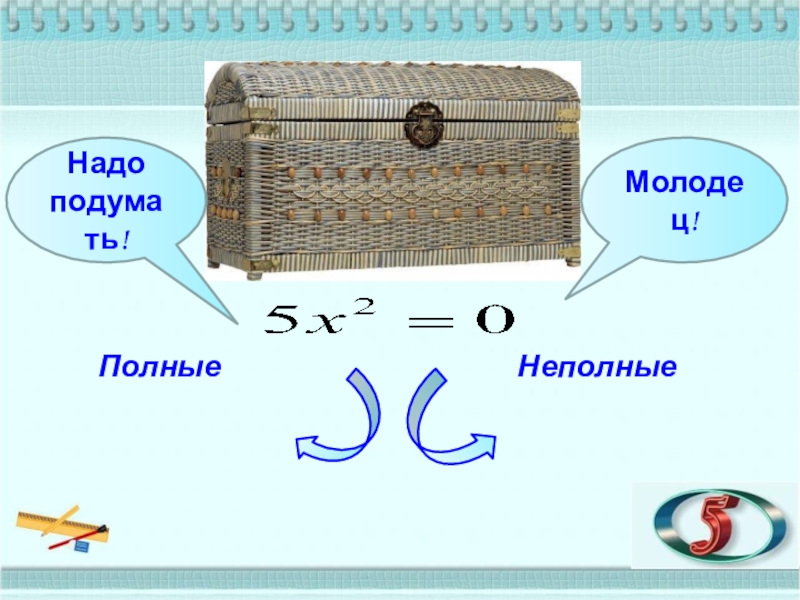
- 10. ПолныеНеполныеМолодец!Надо подумать!
- 11. ПолныеНеполныеМолодец!Надо подумать!
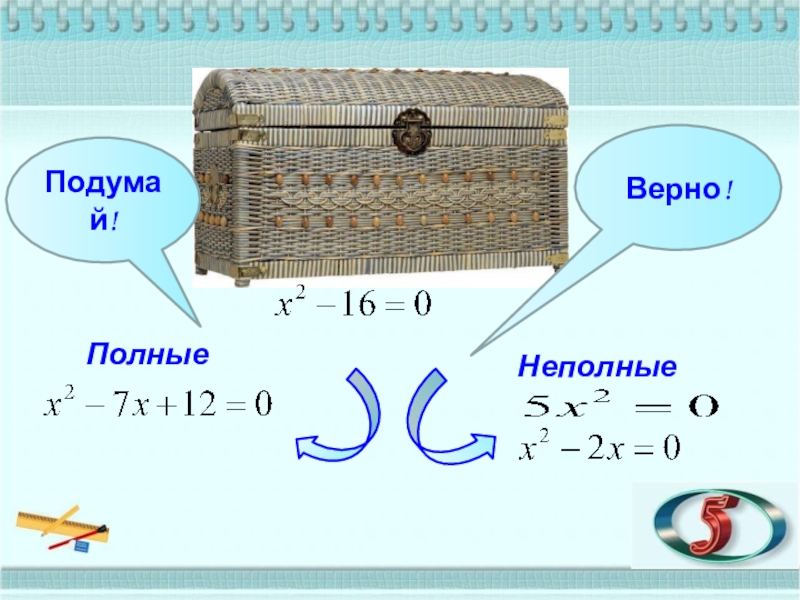
- 12. ПолныеНеполныеПодумай!Верно!
- 13. ПолныеНеполныеПодумай!Верно!
- 14. ПолныеНеполныеМолодец!Надо подумать!
- 15. Квадратное уравнение имеет 2 действительных корняКвадратное уравнение
- 16. Формулы корней квадратного уравненияВид уравненияФормулы корней
- 17. Т е о р е м а
- 18. Теорема обратная теореме Виета.Если числа m и
- 19. Нечётные партыЧётные парты1. Найти корни приведённых квадратных
- 20. Нечётные партыЧётные парты1. Найти корни приведённых квадратных
- 21. Для снятия перегрузки организма. Шеей крутим
- 22. ИсследованиеРебята, посмотрите на эти уравнения и их
- 23. Франсуа Виет (1540 –
- 24. Свойства коэффициентов квадратного уравненияЕсли в уравнении
- 25. “Я слышу – я забываю, я
- 26. Самостоятельная работа1вариант2 вариант1. Сумма корней квадратного уравнения
- 27. Слайд 27
- 28. Самооценка за урок12-15 пятёрок = «золотая пятёрка»9-11
- 29. РефлексияО чем сегодня мы говорили на уроке?Узнали
- 30. Вершина знаний высокаИ к ней ступенек много.Пусть
Слайд 1МКОУ Воскресенская средняя общеобразовательная школа
Квадратные уравнения
Урок обобщающего повторения
Учитель математики Палилова Алла
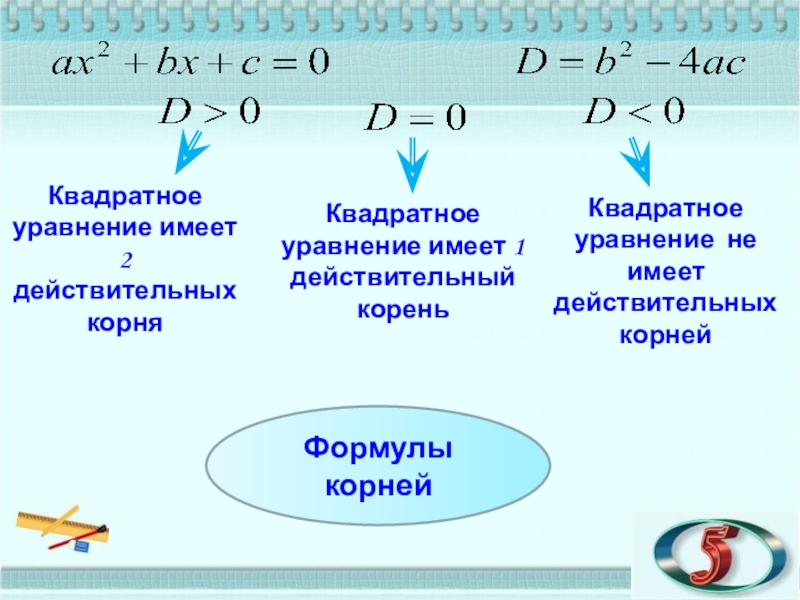
Слайд 15Квадратное уравнение имеет 2 действительных корня
Квадратное уравнение имеет 1 действительный корень
Квадратное
Формулы корней
Слайд 17Т е о р е м а В и
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Если х1 и х2 ─ корни уравнения
x2 + px + q = 0, то
X1 + X2 = -p
X1 * X2 = q
Слайд 18Теорема обратная теореме Виета.
Если числа m и n таковы, что их
Слайд 19Нечётные парты
Чётные парты
1. Найти корни приведённых квадратных уравнений:
1. Записать приведённое квадратное
2. Разложить квадратный трёхчлен на множители:
2. Разложить квадратный трёхчлен на множители:
3. Сократить дробь:
Слайд 20Нечётные парты
Чётные парты
1. Найти корни приведённых квадратных уравнений:
1. Записать приведённое квадратное
2. Разложить квадратный трёхчлен на множители:
2. Разложить квадратный трёхчлен на множители:
3. Сократить дробь:
Слайд 21Для снятия перегрузки организма.
Шеей крутим осторожно -
Голова кружиться может.
Так. И вправо посмотри.
Вверх посмотрим, повернёмся,
И за работу вновь возьмёмся.
Слайд 22Исследование
Ребята, посмотрите на эти уравнения и их корни. Попробуйте найти закономерность:
б) в соответствии между отдельными
коэффициентами и их корнями:
в) в сумме коэффициентов:
Уравнения Корни a + b + c
х2 + 2х ─ 3 =0 х1 = ─3, х2 = 1 1+2-3=0
х2 ─ 7х + 6 = 0 х1= 1, х2 = 6 1-7+6=0
4х2 ─7х +3 =0 х1=3/4 , х2=1 4-7+3=0
5х2─ х ─ 4 =0 х1=-4/5 , х2=1 5-1-4=0
Слайд 23
Франсуа Виет (1540 – 1603)
Именно этим французским математиком впервые были
Формулы, выражающие зависимость корней от его коэффициентов, были выведены Виетом в 1591г.
Слайд 24Свойства коэффициентов квадратного уравнения
Если в уравнении ax2 + bx +
a + b + c = 0, то х1= 1, х2 = с/а а + с – в = 0, то х1= -1, х2 = - с/а
Решите уравнение
197x2 - 2197x + 2000 = 0
Слайд 26Самостоятельная работа
1вариант
2 вариант
1. Сумма корней квадратного уравнения равна
2. Произведение корней квадратного
3. Сколько действительных корней имеет квадратное уравнение
4. Найдите корни квадратного уравнения
5. Найдите все значения а при которых квадратное уравнение
имеет два различных корня
не имеет корней
-4
-5
2
1; 0,25
-5
3
0
1; 2/3
a <25
a >25
Слайд 28Самооценка за урок
12-15 пятёрок = «золотая пятёрка»
9-11 пятёрок = «серебряная пятёрка»
6-8
Менее 6 пятёрок = «право на помощь со стороны обладателя золотой пятёрки или учителя»
Слайд 29Рефлексия
О чем сегодня мы говорили на уроке?
Узнали ли вы что –то
Довольны ли вы своей работой на уроке?
Вам было интересно на уроке?
Слайд 30Вершина знаний высока
И к ней ступенек много.
Пусть будет к знаниям всегда
Успешною
Благодарю всех за урок, урок окончен.