которая когда – нибудь не окажется применимой к явлениям действительного мира
Н. И Лобачевский
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Интеграл.
Содержание
- 1. Презентация по теме Интеграл.
- 2. Определенный интеграл Разность
- 3. Названия символовa – нижний предел интегрированияb –
- 4. Формула Ньютона - Лейбница
- 5. Геометрический смысл интеграла
- 6. Основные свойства интеграла
- 7. Слайд 7
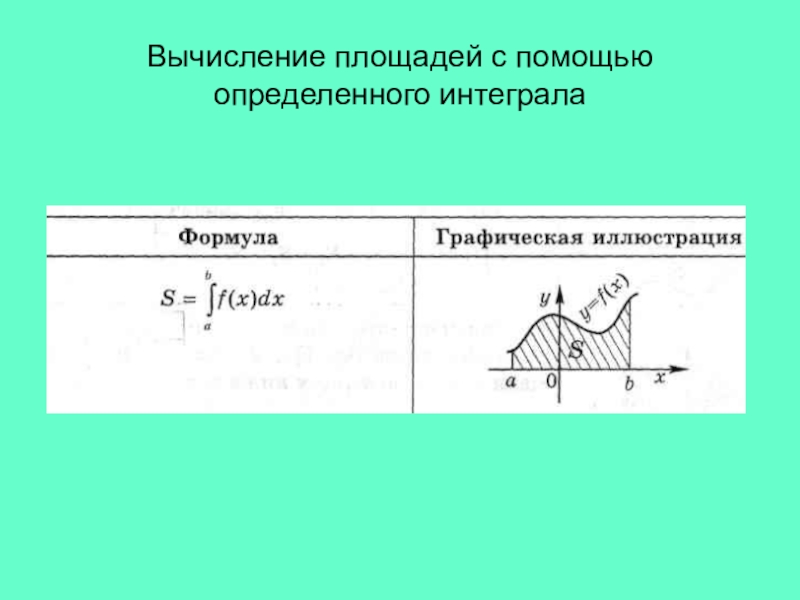
- 8. Вычисление площадей с помощью определенного интеграла
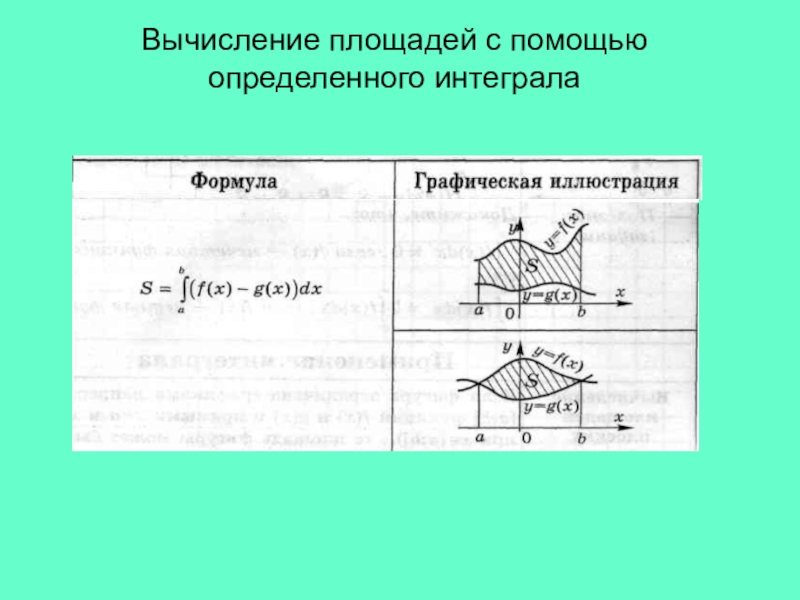
- 9. Вычисление площадей с помощью определенного интеграла
- 10. Вычисление площадей с помощью определенного интеграла
- 11. Схема решения задач на вычисление площадей фигур
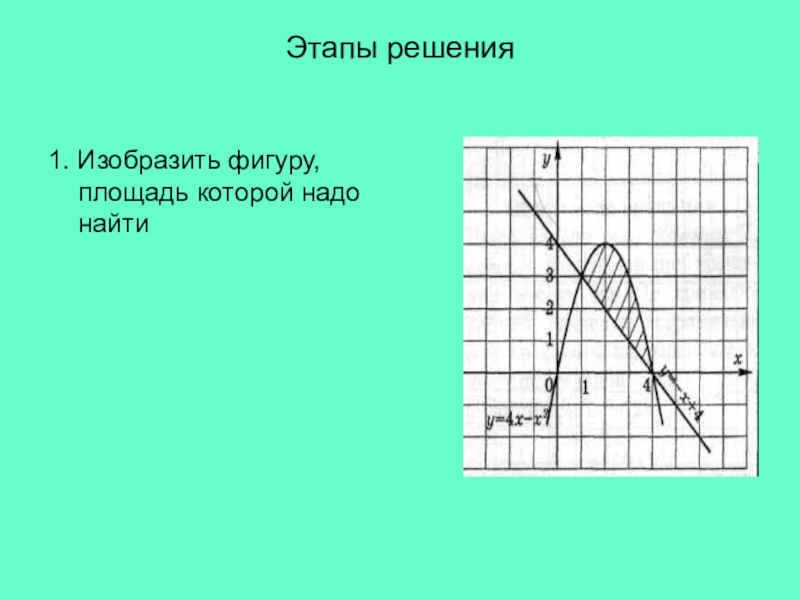
- 12. Этапы решения1. Изобразить фигуру, площадь которой надо найти
- 13. Этапы решения2. Найдите абсциссы точек пересечения графиков
- 14. Этапы решения3.Найдите площадь фигуры по формуле
- 15. Этапы решения4. Запишите ответ
- 16. Вычислить интегралы1 вариант2 вариант1)2)3)1)2)3)4)4)5)5)6)6)
- 17. 1 вариант2 вариант7)7)8)9)10)11)8)9)10)11)
- 18. Вычислить площадь фигуры ограниченной линиями1 вариант2 вариант1)2)3)1)2)3)и
Определенный интеграл Разность называют интегралом от функции на отрезке и обозначают так:
Слайд 3Названия символов
a – нижний предел интегрирования
b – верхний предел интегрирования
- знак интеграла
- подынтегральная функция
x – переменная интегрирования
- подынтегральное выражение
- подынтегральная функция
x – переменная интегрирования
- подынтегральное выражение
Слайд 11Схема решения задач на вычисление площадей фигур по формуле
Вычислить площадь
фигуры, ограниченной линиями:
Слайд 13Этапы решения
2. Найдите абсциссы точек пересечения графиков функций
и
т.е. решить уравнение
=
т.е. решить уравнение
=
Слайд 18Вычислить площадь фигуры ограниченной линиями
1 вариант
2 вариант
1)
2)
3)
1)
2)
3)
и Ох
и
и
и
и
и Ох