- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Графики тригонометрических функций
Содержание
- 1. Презентация по теме Графики тригонометрических функций
- 2. тригонометрические функцииГрафиком функции у = sin x
- 3. Преобразование графиков тригонометрических функцийтригонометрические функцииy= sin x +πвспомнить правила
- 4. Преобразование графиков тригонометрических функцийтригонометрические функцииГрафик функции
- 5. Преобразование графиков тригонометрических функцийтригонометрические функциивспомнить правила Как будет выглядеть график функции y =sin (x+ π/4)
- 6. Преобразование графиков тригонометрических функцийтригонометрические функцииy =sin (x+ π/4)Как будет выглядеть график функцииy=sin (x - π/6)
- 7. Преобразование графиков тригонометрических функцийтригонометрические функцииy =sin (x - π/6)
- 8. Преобразование графиков тригонометрических функций путем сжатия и
- 9. Преобразование графиков тригонометрических функций путем сжатия и растяжениятригонометрические функцииy=sin2xy=sin4xY=sin0.5xвспомнить правила
- 10. Преобразование графиков тригонометрических функций путем сжатия и
- 11. Преобразование графиков тригонометрических функций путем сжатия и растяжениятригонометрические функцииy = cos2xy = cos 0.5xвспомнить правила
- 12. Преобразование графиков тригонометрических функций путем сжатия и
- 13. Преобразование графиков тригонометрических функций путем сжатия и растяжениятригонометрические функцииy = -sin3xy = sin3xвспомнить правила
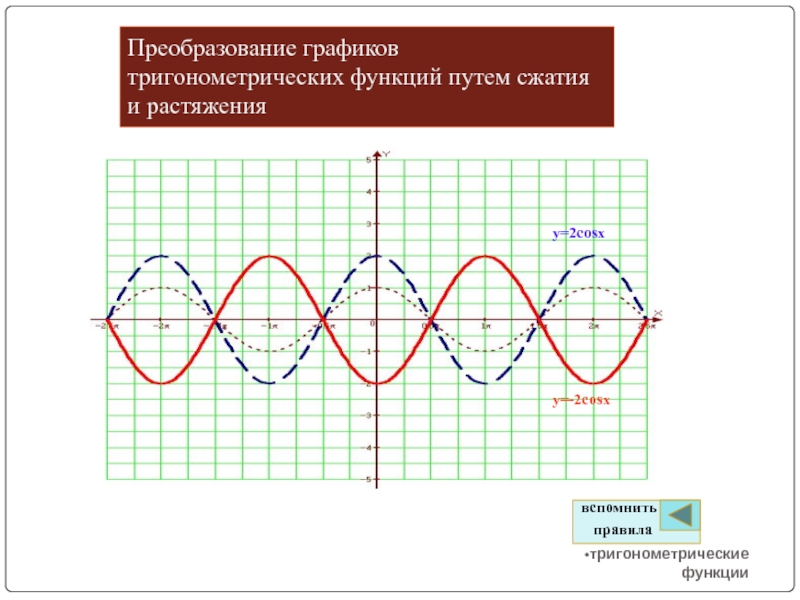
- 14. Преобразование графиков тригонометрических функций путем сжатия и растяжениятригонометрические функцииy=2cosxy=-2cosxвспомнить правила
- 15. Теперь вы можете преобразовывать графики самостоятельно!тригонометрические функции
- 16. тригонометрические функцииСпасибо за внимание!
тригонометрические функцииГрафиком функции у = sin x является синусоидаСвойства функции:D(y) =R, Е(у)=[-1;1]Периодическая (Т=2π)Функция нечетная: sin(-x)=- sin xНули функции: х = πn, n∈Zy=sin x
Слайд 2тригонометрические функции
Графиком функции у = sin x является синусоида
Свойства функции:
D(y) =R,
Е(у)=[-1;1]
Периодическая (Т=2π)
Функция нечетная: sin(-x)=- sin x
Нули функции:
х = πn, n∈Z
Периодическая (Т=2π)
Функция нечетная: sin(-x)=- sin x
Нули функции:
х = πn, n∈Z
y=sin x
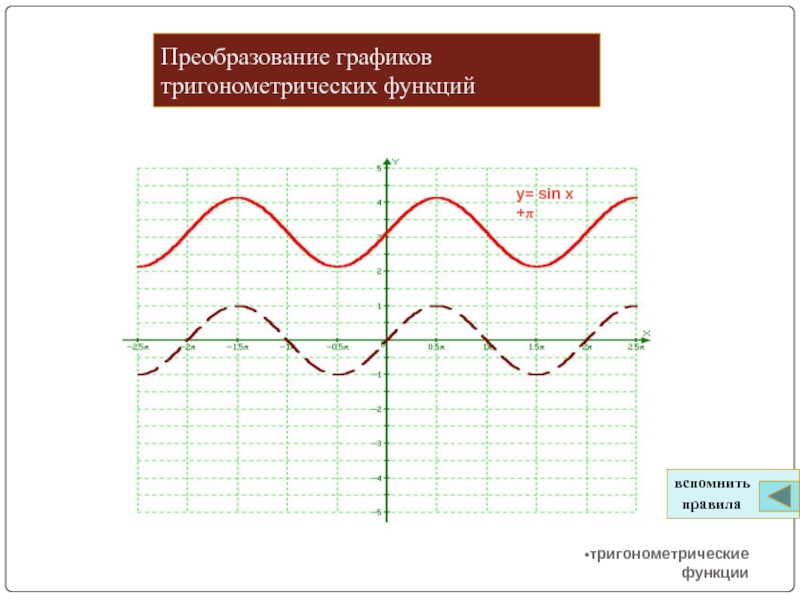
Слайд 3Преобразование графиков тригонометрических функций
тригонометрические функции
y= sin x +π
вспомнить
правила
Слайд 4Преобразование графиков
тригонометрических функций
тригонометрические функции
График функции у = f (x+в) получается
из графика функции у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс
График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат
График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат
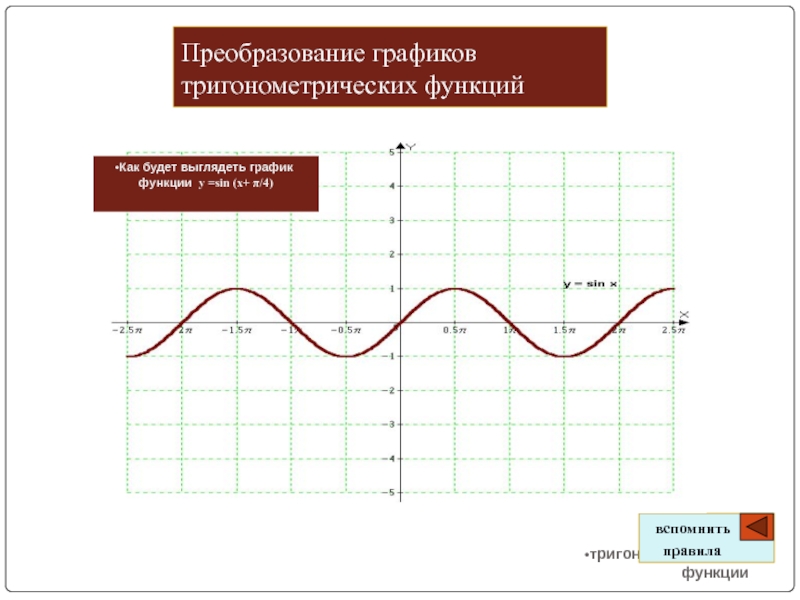
Слайд 5Преобразование графиков тригонометрических функций
тригонометрические функции
вспомнить
правила
Как будет выглядеть график функции
y =sin (x+ π/4)
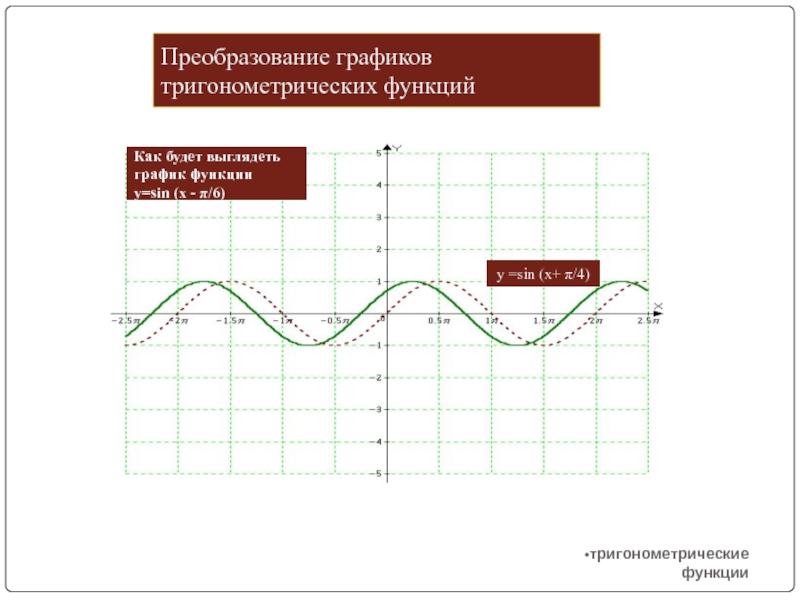
Слайд 6Преобразование графиков тригонометрических функций
тригонометрические функции
y =sin (x+ π/4)
Как будет выглядеть
график
функции
y=sin (x - π/6)
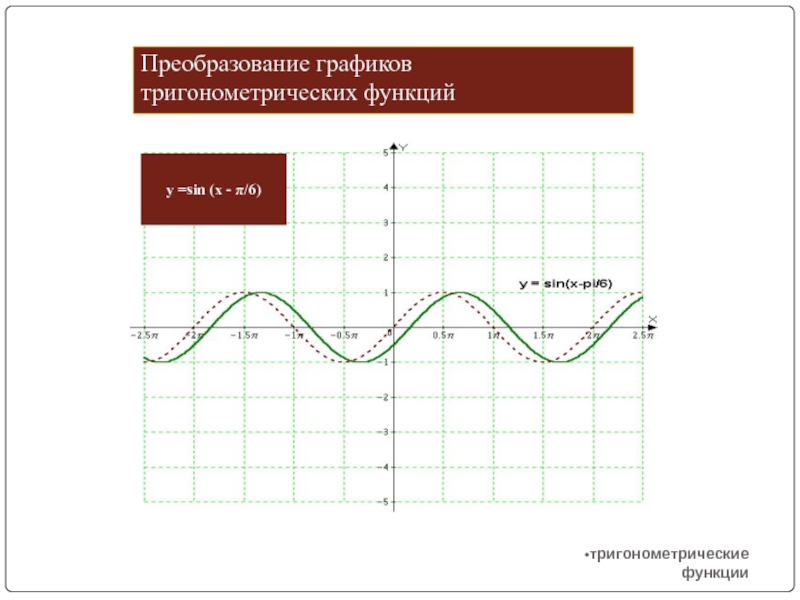
y=sin (x - π/6)
Слайд 8Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
График функции у
=k f (x) получается из графика функции у = f(x) путем его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0
График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0
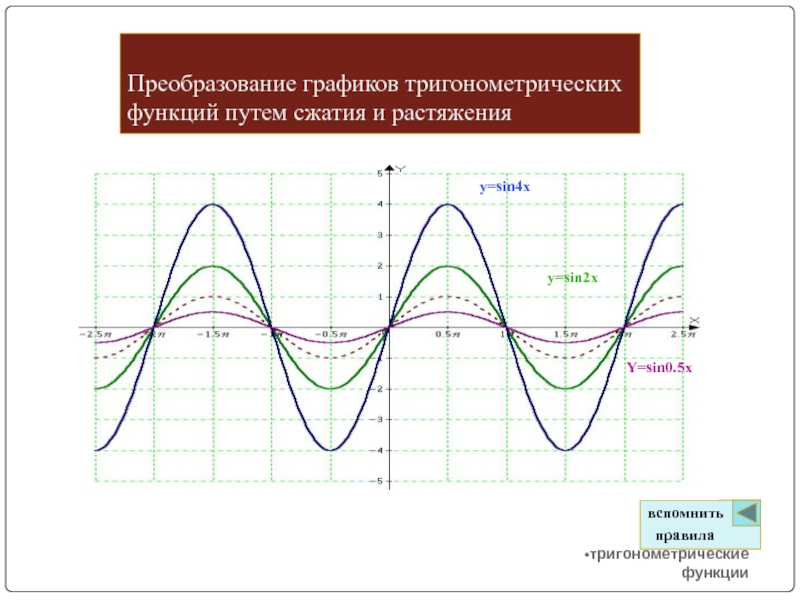
Слайд 9Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
y=sin2x
y=sin4x
Y=sin0.5x
вспомнить
правила
Слайд 10Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
График функции у
= f (kx) получается из графика функции у = f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз (при 0
График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз (при 0
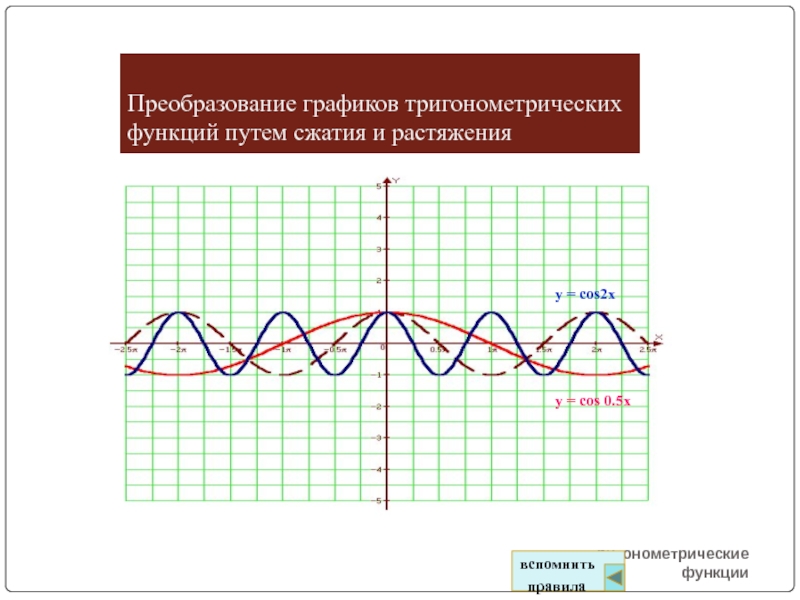
Слайд 11Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
y = cos2x
y
= cos 0.5x
вспомнить
правила
Слайд 12Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
Графики функций у
= -f (kx) и у=-k f(x) получаются из графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
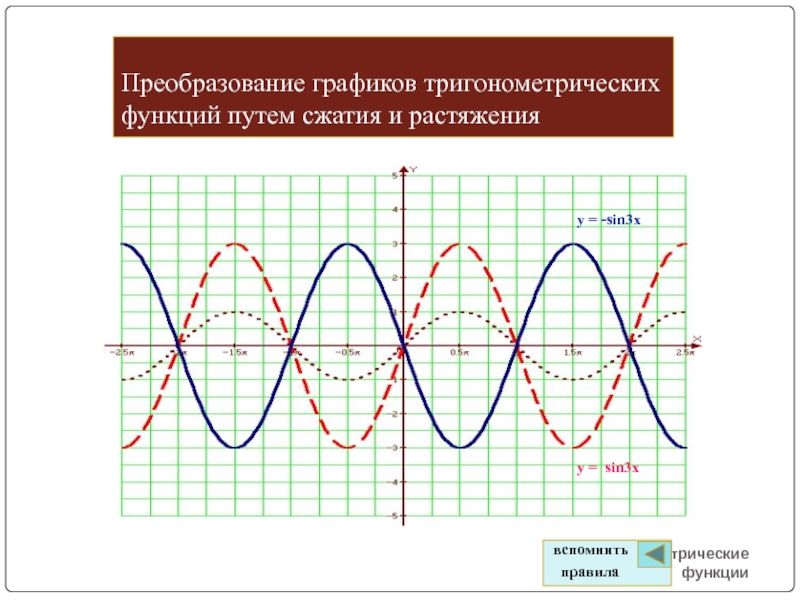
Слайд 13Преобразование графиков тригонометрических функций путем сжатия и растяжения
тригонометрические функции
y = -sin3x
y
= sin3x
вспомнить
правила
![Презентация по теме Графики тригонометрических функций тригонометрические функцииГрафиком функции у = sin x является синусоидаСвойства функции:D(y) =R, тригонометрические функцииГрафиком функции у = sin x является синусоидаСвойства функции:D(y) =R, Е(у)=[-1;1]Периодическая (Т=2π)Функция нечетная: sin(-x)=- sin xНули](/img/thumbs/900afbefcec99b7a2c44d22d69b3d822-800x.jpg)