- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме :экстремальные задачи
Содержание
- 1. Презентация по теме :экстремальные задачи
- 2. Так как здание всего мира совершенно и
- 3. Экстремальными задачами называют задачи на нахождение наибольших
- 4. Задача 1. Дана прямая c и точка
- 5. Задача 2. Дана окружность с центром в
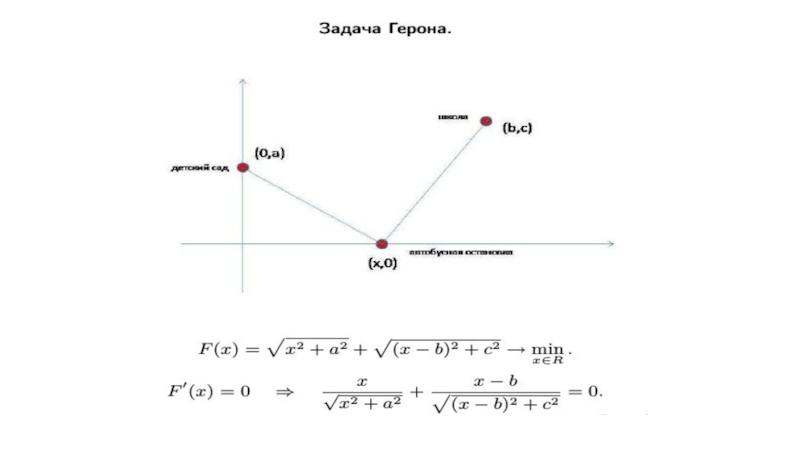
- 6. Задача 3 (задача Герона). Дана прямая с
- 7. Идея нахождения искомой точки C состоит в
- 8. Задача 4 Дан остроугольный треугольник ABC,
- 9. В начале XIX в. немецкий геометр Якоб
- 10. Задача 5 В плоскости даны три точки
- 11. Задача 6. Из скважин A, B, C
- 12. Для построения минимальной сети достаточно найти так
- 13. Задача 7.Пусть L—окружность с центром в точке
- 14. Второй случай . Если треугольник АВС имеет
- 15. Задача 8. Площадь треугольника АВ`С равна S.
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Решена ли задача Дидоны?Если подходить к вопросу
- 22. С практической точки зрения ситуация, в которой
- 23. ВЫВОДЫЭкстремальные задачи интересны своей нестандартностью, красотой, индивидуальностью,
Слайд 2Так как здание всего мира совершенно и возведено премудрым Творцом, то
максимума или минимума.
Л.Эйлер
Слайд 3Экстремальными задачами называют задачи на нахождение наибольших и наименьших значений. Эти
Слайд 4Задача 1. Дана прямая c и точка A, ей не принадлежащая.
Решение. Искомой точкой C является основание перпендикуляра, опущенного из точки A на прямую c (рис. 1). Действительно, для любой другой точки C’, принадлежащей прямой c отрезок AC’ будет наклонной и, значит его длина AC’ будет больше длины перпендикуляра AC. Точки D, для которой расстояние CD наибольшее, не существует.
Слайд 5Задача 2. Дана окружность с центром в точке O и радиусом
Решение. Искомыми точками будут точки пересечения прямой AO с окружностью (рис. 2). Действительно, для точки D’ окружности, отличной от D, имеем: AD = AO + OD = AO + OD’ > AD’. Аналогичным образом доказывается, что для любой точки C’ окружности, отличной от C имеет место неравенство AC < AC’.
Слайд 6Задача 3 (задача Герона). Дана прямая с и две точки А
Решение. Если бы точки A и B лежали по разные стороны от прямой c (рис. 3,а), то искомой точкой C была бы точка пересечения отрезка AB и прямой c. Действительно, для любой другой точки C’ прямой c будет выполняться неравенство AC + CB = AB < AC’ + C’B и, следовательно, сумма AC + CB будет наименьшей. Пусть теперь точки A и B лежат по одну сторону от прямой c (рис. 3,б).
Слайд 7Идея нахождения искомой точки C состоит в замене точки B на
Из этого можно вывести закон отражения света. А именно, известно, что луч света распространяется по кратчайшему пути. Поэтому, если луч света исходит из точки A, отражается от прямой c и приходит в точку B, то точка C будет точкой отражения и, таким образом, имеет место закон отражения света: угол падения светового луча равен углу отражения.
Слайд 8Задача 4 Дан остроугольный треугольник ABC, AP⊥ BC, BQ ⊥
Решение Сначала докажем следующее свойство высотного треугольника: QR+RP обращается в минимум лишь в случае , если QR и RP образуют с AB равные углы (последние следует из задачи Герона).
Слайд 9В начале XIX в. немецкий геометр Якоб Штейнер исследовал проблему минимизации
Например, необходимо три пункта A, B, C соединить системой дорог так, чтобы общая протяженность построенных дорог была минимальной. В более корректной математической постановке проблема Штейнера формулируется следующим образом.
Слайд 10
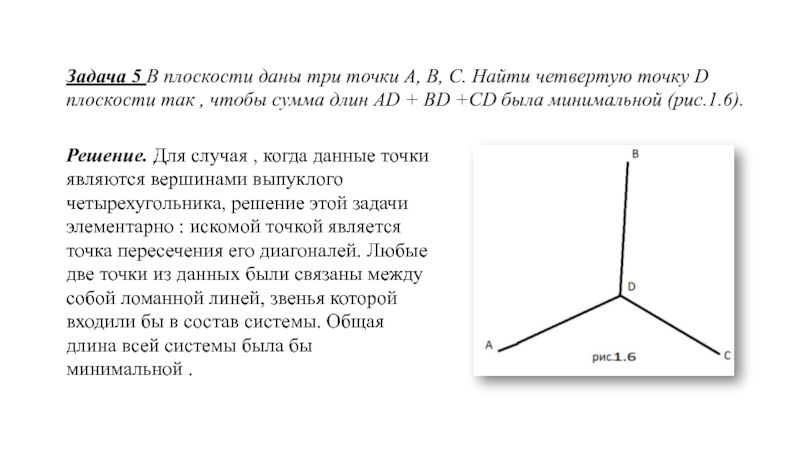
Задача 5 В плоскости даны три точки A, B, C. Найти
Решение. Для случая , когда данные точки являются вершинами выпуклого четырехугольника, решение этой задачи элементарно : искомой точкой является точка пересечения его диагоналей. Любые две точки из данных были связаны между собой ломанной линей, звенья которой входили бы в состав системы. Общая длина всей системы была бы минимальной .
Слайд 11Задача 6. Из скважин A, B, C выделяется газ. Соедините их
Обозначим скважины A, B, C точками плоскости. Если бы точки A, B, и C принадлежали одной прямой , то минимальную длину бы имел отрезок , соединяющий крайние точки. Поэтому будем считать, что данные три точки не принадлежат одной прямой . Точки A, B, C определяют некоторый треугольник ABC. Возможны два случая :1) в ABC величина каждого из углов меньше ; 2)в ABC величина одного из углов не меньше  .
Рассмотрим первый случай . Если соединить трубопроводами точки A c B, B c C, C c A, то, оказывается, что длина всей сети отрезков , т. е. AB+ BC + +CA , не будут наименьшей из всех возможных сетей, соединяющих точки A, B и C. Если длины сторон AB=c , BC=a , AC=b треугольника связаны зависимостью a ≤ b ≤ c , то найдется ломаная линия короче указанной (длина этой ломанной равна a+b ) , но оказывается возможным соединить точки A, B и C еще более короткой сетью .
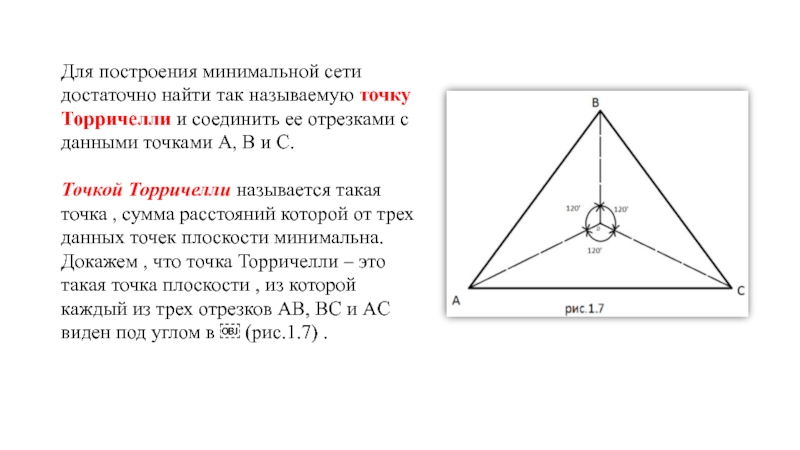
Слайд 12Для построения минимальной сети достаточно найти так называемую точку Торричелли и
Точкой Торричелли называется такая точка , сумма расстояний которой от трех данных точек плоскости минимальна. Докажем , что точка Торричелли – это такая точка плоскости , из которой каждый из трех отрезков AB, BC и AC виден под углом в  (рис.1.7) .
Слайд 13Задача 7.Пусть L—окружность с центром в точке С и радиусом R=CD
Из обобщения теоремы Герона (если заменить прямую дугой окружности ) следует, что AD + DB должны образовывать равные углы с окружностью , а значит и радиусом DC. Повторяя эти рассуждения для двух других точек A и B , убеждаемся , что углы , образованные отрезками AD, BD, CD друг с другом , должны быть равные , т. е. равны по величине  . доказательство было построено на допущении, что две остальные точки были вне круга. Но иначе и быть не может . Пусть точка A находится внутри окружности L, тогда AC ≤CD.В Этом случае при любом расположении точек A, B, D AD+BD≥AB и AD + BD+ CD ≥AB+ AC. Последнее неравенство показывает , что минимальное значение суммы AD + BD+ CD получится , если D совпадает с А , но это противоречит нашему допущению. Значит, что точка находится вне круга.Итак, для отыскания точки D строим на каждый из сторон AB, BC, AC треугольника ABC сегмент, вмещающий угол в  . точка пересечения дуг сегментов – искомая точка (достаточно построить два сегмента).
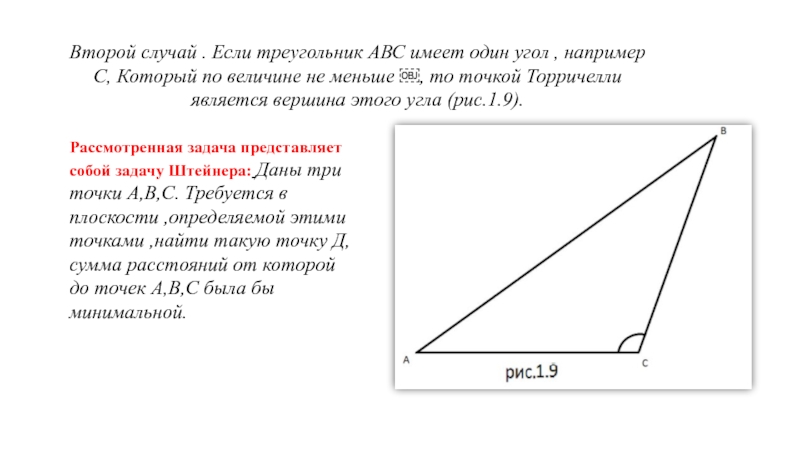
Слайд 14Второй случай . Если треугольник АВС имеет один угол , например
Рассмотренная задача представляет собой задачу Штейнера: Даны три точки А,В,С. Требуется в плоскости ,определяемой этими точками ,найти такую точку Д, сумма расстояний от которой до точек А,В,С была бы минимальной.
Слайд 15Задача 8. Площадь треугольника АВ`С равна S. Укажите такой треугольник со
Решение .
На рисунке 1.10 показан AB’C с площадью S=ACH. Заданную площадь треугольника определяет сторона и высота H. Проведем через точку B’ прямую MN, параллельную AC. Теперь задачу можно сформулировать так: на прямой MN найдите точку B, чтобы сумма AB+BC была наименьшей, для случая, когда две точки A и C расположены в одной полуплоскости с границей MN на одном и том же расстоянии от MN. Из задачи Герона следует, что AB=BC, т.е. ABC -равнобедренный.
Слайд 21Решена ли задача Дидоны?
Если подходить к вопросу утилитарно, то ответ, конечно,
C Дидоной связывают изучение изопериметрических задач геометрии, приведшее впоследствии к вариационному исчислению и современным концепциям оптимального управления и теории экстремальных задач. Сложилось довольно стойкое убеждение, что задача Дидоны — исторический анекдот, а не проблема современной науки. В реальности дело обстоит совсем иначе. Гипотеза о том, что у математики есть метод решения задачи Дидоны, с теоретической точки зрения критики не выдерживает.
Слайд 22С практической точки зрения ситуация, в которой Дидона должна была принять
Задача Дидоны, вдохновлявшая наших предков, остается таким же интеллектуальным вызовом, как кантовские звездное небо и моральный закон.
Слайд 23ВЫВОДЫ
Экстремальные задачи интересны своей нестандартностью, красотой, индивидуальностью, постановкой вопроса. Они требуют
Общее в решении экстремальных задач заключается в самом характере применения того или иного мате математического метода, т. к. математические методы применяются к математическим моделям того или иного явления. Ведь математика - это универсальный язык науки и техники, средство моделирования процессов и явлений.