- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математикеГеометрический смысл определённого интеграла. Площадь криволинейной трапеции.
Содержание
- 1. Презентация по математикеГеометрический смысл определённого интеграла. Площадь криволинейной трапеции.
- 2. Определенный интегралДостаточное условие существование определенного интеграла: если
- 3. Свойства определенного интеграла1) Если переставить пределы интегрирования, то
- 4. Свойства определенного интеграла4) Определенной интеграл от алгебраической суммы
- 5. Свойства определенного интеграла6) Если a ≤ b, а f(x) и u·g(x) - две
- 6. Свойства определенного интеграла8) Если m и M – наименьшее и наибольшее значения
- 7. Геометрический смысл Определенный интеграл как функция верхнего
- 8. Криволинейная трапеция Фигура, ограниченная осью абцисс
- 9. Формула Ньютона-ЛейбницаФормула Ньютона-Лейбница - даёт соотношение между операциями
Слайд 2Определенный интеграл
Достаточное условие существование определенного интеграла: если функция y = f(x)
Если существует конечный предел интегральной суммы который не зависит ни от разбиения отрезка [a;b], ни от выбора точек частичных отрезков, то этот предел называется – определенным интегралом.
Слайд 3Свойства определенного интеграла
1) Если переставить пределы интегрирования, то изменится лишь знак:
2) Каковы
3) Постоянный множитель А выносится за знак определенного интеграла:
Слайд 4Свойства определенного интеграла
4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций
5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a Замечание: если f(x) ≤0 на [a;b] и a
Если f(x) ≤0 на [a;b], то ≥0
Слайд 5Свойства определенного интеграла
6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на
, т.е. неравенство почленно интегрируется.
7) Если a ≤ b и f(x) непрерывна на [a, b], то:
, т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
Слайд 6Свойства определенного интеграла
8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b],
9) Теорема о среднем:
Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство:
10) Определенный интеграл с одинаковыми пределами равен 0.
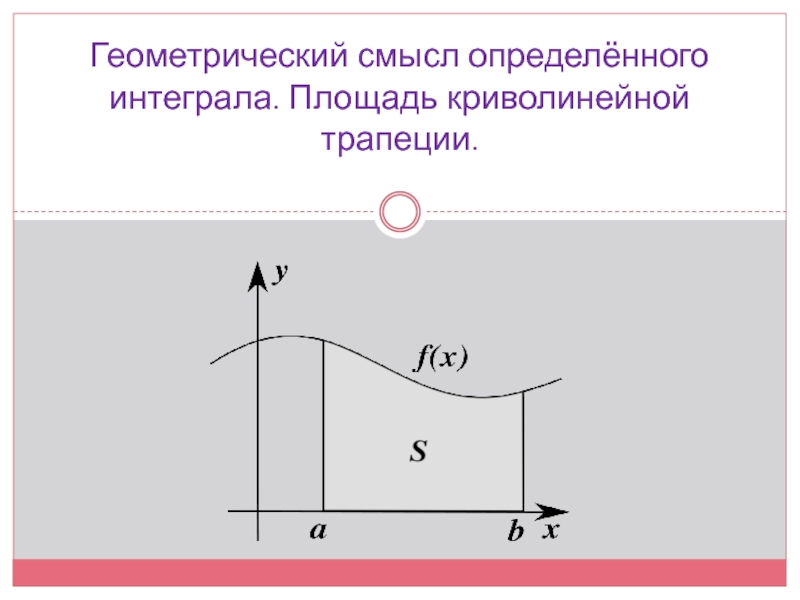
Слайд 7Геометрический смысл
Определенный интеграл как функция верхнего предела:
В отличие
Интеграл с переменным верхним пределом есть функция своего верхнего предела Ф(х):
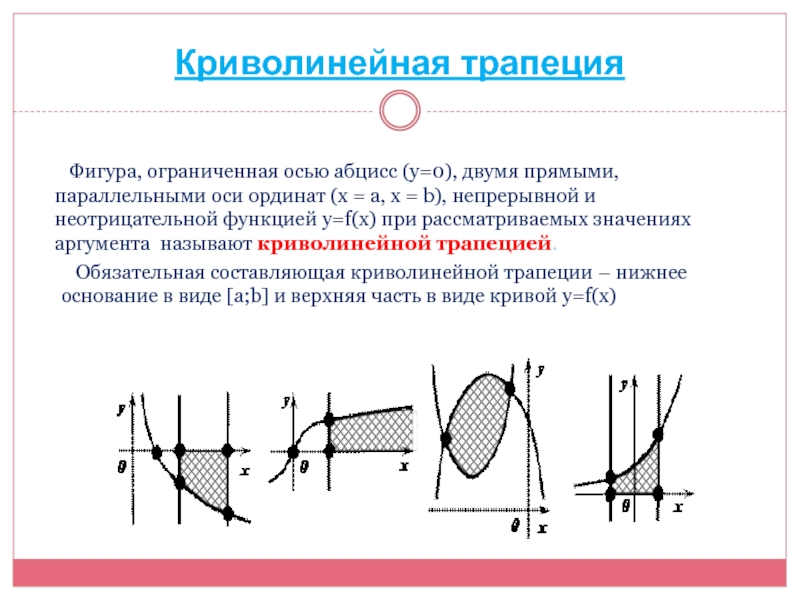
Слайд 8Криволинейная трапеция
Фигура, ограниченная осью абцисс (у=0), двумя прямыми, параллельными
Обязательная составляющая криволинейной трапеции – нижнее основание в виде [a;b] и верхняя часть в виде кривой y=f(x)
Слайд 9Формула Ньютона-Лейбница
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F- первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
![Презентация по математикеГеометрический смысл определённого интеграла. Площадь криволинейной трапеции. Определенный интегралДостаточное условие существование определенного интеграла: если функция y = f(x) Определенный интегралДостаточное условие существование определенного интеграла: если функция y = f(x) непрерывна на [a;b], то она интегрируема](/img/thumbs/a2704f18c167c342ed94c33b3fb3ff69-800x.jpg)


![Презентация по математикеГеометрический смысл определённого интеграла. Площадь криволинейной трапеции. Свойства определенного интеграла6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на Свойства определенного интеграла6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то:, т.е. неравенство](/img/thumbs/e4ab4128465226ce26773cf3c7abed8a-800x.jpg)
![Презентация по математикеГеометрический смысл определённого интеграла. Площадь криволинейной трапеции. Свойства определенного интеграла8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], Свойства определенного интеграла8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то:9) Теорема о среднем:Если функция f(x) непрерывна](/img/thumbs/79ccb989f37ec8b7afff359a6b5cb6ed-800x.jpg)