- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Вводное повторение. Квадратные неравенства (9 класс
Содержание
- 1. Презентация по математике Вводное повторение. Квадратные неравенства (9 класс
- 2. Квадратные неравенстваКвадратным называетсянеравенство, левая часть которого −квадратный
- 3. Решением неравенства с одним неизвестным называется
- 4. Являются ли следующие неравенства квадратными? А)
- 5. Как разложить квадратный трёхчлен ax2+bx+cна множители?ax2+bx+c= a(x-x1 )(x-x2)
- 6. Основные способы решения квадратных неравенств:Графический методМетод интервалов
- 7. Графический метод решения квадратного неравенства:1) Определить направление
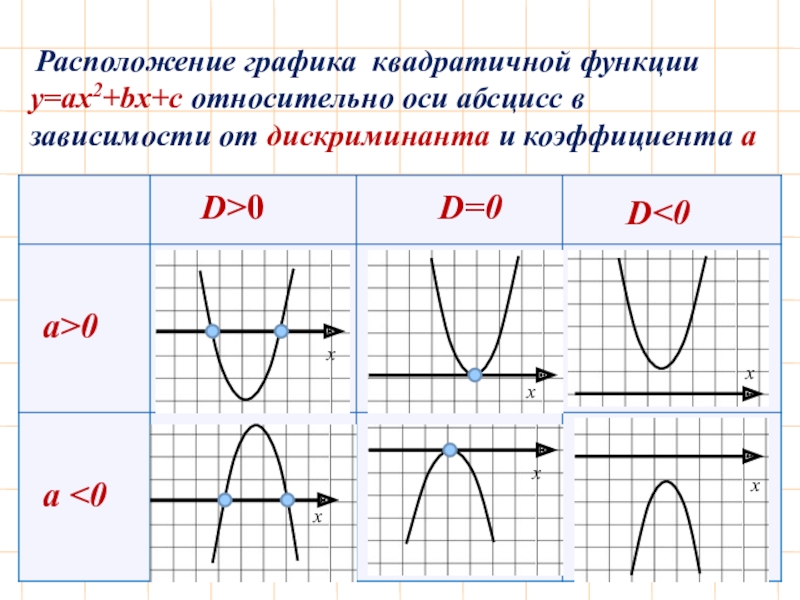
- 8. D>0D=0D0а
- 9. -13yxу= х2 - 2х - 3
- 10. Решите графически неравенства: 1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞)
- 11. Разложить квадратный трехчлен на множители, воспользовавшись формулой
- 12. Пример1) решим соответствующее квадратное уравнениех² + 5х
- 13. Решите неравенства методом интервалов : 1) х(х+7)≥0; 2) (х-1)(х+2)≤0; 3) х- х²+20; 5) х(х+2)
- 14. Домашнее задание.№ 606(2,4,6,8), 608 (2,4,6)
Слайд 2Квадратные неравенства
Квадратным называется
неравенство, левая часть которого −
квадратный трёхчлен, а правая часть
равна
ах²+bх+с>0 ах²+bх+с≥0
ах²+bх+с<0 ах²+bх+с≤0
Слайд 3Решением неравенства с одним неизвестным называется то значение неизвестного, при
Решить неравенство − это значит найти все его решения или установить, что их нет.
Слайд 4Являются ли следующие неравенства квадратными?
А) 4у² - 5у +7
Б) 2х - 4 > 0
В) 4х² - 2х ≥ 0
Г) 3у – 5у² + 7 < 0
Д) 4 – 6х + 5х² ≤ 0
Е) 5у⁴ +3у - 6 < 0
Слайд 7Графический метод решения квадратного неравенства:
1) Определить направление ветвей параболы, по
2) Найти корни соответствующего квадратного уравнения (нули функции);
3) Построить эскиз графика.
4) Учитывая знак неравенства, выписать ответ.
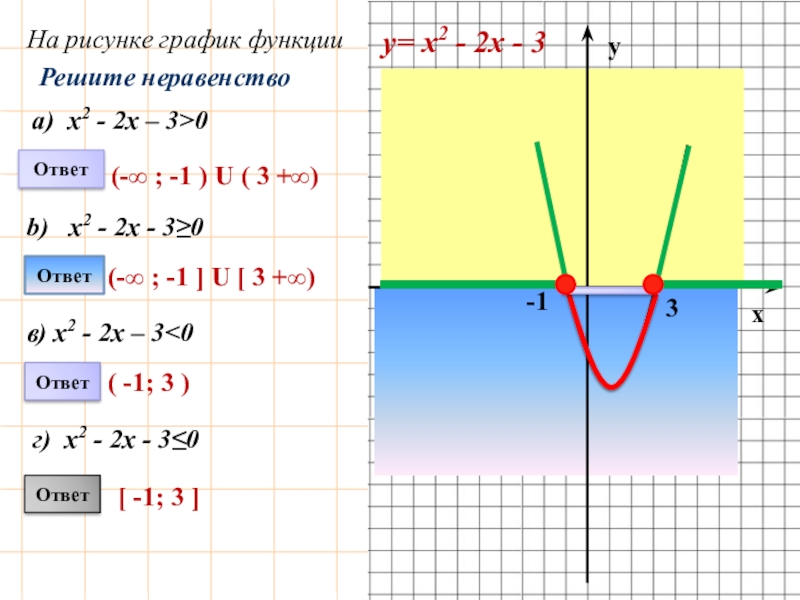
Слайд 9-1
3
y
x
у= х2 - 2х - 3
Решите неравенство
a)
b) х2 - 2х - 3≥0
в) х2 - 2х – 3<0
г) х2 - 2х - 3≤0
Ответ
(-∞ ; -1 ) U ( 3 +∞)
Ответ
[ -1; 3 ]
Ответ
( -1; 3 )
Ответ
(-∞ ; -1 ] U [ 3 +∞)
На рисунке график функции
Слайд 10Решите графически неравенства:
1) х²-3х0;
3) х²+2х≥0;
4) -2х²+х+1≤0
Проверим ответы:
(0;3)
(-∞;0)U(4;+∞)
(-∞; -2]U[0; +∞)
(-∞; -
Слайд 11Разложить квадратный трехчлен на множители, воспользовавшись формулой ах2+вх+с=а(х-х1)(х-х2);
Найти корни многочлена;
Изобразить их
Разбить числовую прямую на интервалы;
Определить знаки множителей на интервалах;
Выбрать промежутки нужного знака;
Записать ответ (с помощью скобок или знаков неравенства).
Алгоритм решения неравенств методом интервалов
Слайд 12Пример
1) решим соответствующее квадратное уравнение
х² + 5х – 6 = 0.
х
Значит, х² + 5х – 6 = (х−1)(х+6)
2)
3) Запишем ответ: (-∞; -6]U[1; +∞)
Дано неравенство: х² + х – 6 ≥ 0
Решение:
х
- 6
1
−
+
+
Слайд 13
Решите неравенства методом интервалов :
1) х(х+7)≥0;
2) (х-1)(х+2)≤0;
3) х-
4) -х²-5х+6>0;
5) х(х+2)<15
Проверим ответы:
1) (-∞;-7]U[0; +∞)
2) [-2;1]
3) (-∞;-1)U(2; +∞)
4) (-6;1)
5) (-5;3)







![Презентация по математике Вводное повторение. Квадратные неравенства (9 класс Решите графически неравенства: 1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞) Решите графически неравенства: 1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞)](/img/thumbs/8c39871df51dcca85df0b9a4acd5281b-800x.jpg)









