МАТЕМАТИКА 11 КЛАСС
(подготовка к ЕГЭ)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Вероятность события 11 класс
Содержание
- 1. Презентация по математике Вероятность события 11 класс
- 2. Классическое определение вероятностиВероятностью события называется отношение числа исходов m, благоприятствующих его наступлению к числу всех исходов n (несовместных): Р(А)=m/n
- 3. На тарелке 16 пирожков: 7 с рыбой,
- 4. На конференцию приехали 3 ученых из Норвегии,
- 5. Вася, Петя, Коля и Лёша бросили жребий
- 6. В некотором городе из 5000 появившихся на
- 7. Проводится жеребьёвка Лиги Чемпионов. На первом этапе
- 8. В случайном эксперименте бросают две игральные кости.
- 9. В случайном эксперименте симметричную монету бросают дважды.
- 10. За круглый стол на 9 стульев в
- 11. За круглый стол на 5 стульев в
- 12. Механические часы с двенадцатичасовым циферблатом в какой-то
- 13. Механические часы с двенадцатичасовым циферблатом в какой-то
- 14. На клавиатуре телефона 10 цифр, от 0
- 15. Из множества натуральных чисел от 10 до
- 16. СобытияСовместные и несовместныеЗависимые и независимыеСумма Произведение Классификация
- 17. Несовместные событияРассмотрим два случайных события A и
- 18. Вообще союз "или" в теории вероятностей можно
- 19. Бросаются два игральных кубика A -
- 20. Вообще союз «и» в теории вероятностей можно
- 21. Совместные событияСлучайные события А и В называются совместными, если в проводимом эксперименте эти события наступают одновременно.
- 22. Случайные события А и В называются независимыми,
- 23. В теории вероятностей события, появления которых не
- 24. ПРИМЕРБросаются два игральных кубика и рассматриваются события:A
- 25. Какое число выпало на 1-м кубике никак
- 26. Р(А * В)=P(A)*P(B)- для независимых событий
- 27. Пример. Допустим, имеется урна с 2 черными
- 28. Случайные события А и В называются зависимыми,
- 29. Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью
- 30. Слайд 30
- 31. Слайд 31
- 32. Два события называются противоположными, если в данном испытании они несовместны
- 33. На экзамене по геометрии школьник отвечает на
- 34. В магазине стоят два платёжных автомата. Каждый
- 35. В торговом центре два одинаковых автомата продают
- 36. В торговом центре два одинаковых автомата продают
- 37. Вероятность того, что батарейка бракованная, равна 0,06.
- 38. Помещение освещается фонарём с тремя лампами. Вероятность
- 39. В магазине стоят два платёжных автомата. Каждый
- 40. В торговом центре два одинаковых автомата продают
- 41. По отзывам покупателей Иван Иванович оценил надёжность
Классическое определение вероятностиВероятностью события называется отношение числа исходов m, благоприятствующих его наступлению к числу всех исходов n (несовместных): Р(А)=m/n
Слайд 1Вероятность события
Климова О.Н., учитель математики высшей квалификационной категории
МБОУ СОШ №108
г. Новосибирска
Слайд 2Классическое определение вероятности
Вероятностью события называется отношение числа исходов m, благоприятствующих его наступлению к
числу всех исходов n (несовместных):
Р(А)=m/n
Р(А)=m/n
Слайд 3На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и
4 с вишней. Юля наугад выбирает
один пирожок. Найдите вероятность того, что он окажется с вишней.
Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Слайд 4На конференцию приехали 3 ученых из Норвегии, 3 из России и
4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Слайд 5Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру.
Найдите вероятность того, что начинать игру должен будет Петя.
Слайд 6
В некотором городе из 5000 появившихся на свет младенцев оказалось 2512
мальчиков. Найдите частоту (вероятность) рождения девочек
Слайд 7Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди
которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Слайд 8В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что
в сумме выпадет 8 очков. Результат округлите до сотых.
Слайд 9В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что
орел выпадет ровно один раз.
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки
Слайд 10За круглый стол на 9 стульев в случайном порядке рассаживаются 7
мальчиков и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
Слайд 11За круглый стол на 5 стульев в случайном порядке рассаживаются 3
мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
Слайд 12Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали
идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 4, но не дойдя до отметки 7 часов.
Слайд 13Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали
идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.
Слайд 14На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность
того, что случайно нажатая цифра будет чётной?
Слайд 15Из множества натуральных чисел от 10 до 19 наудачу выбирают одно
число. Какова вероятность того, что оно делится на 3?
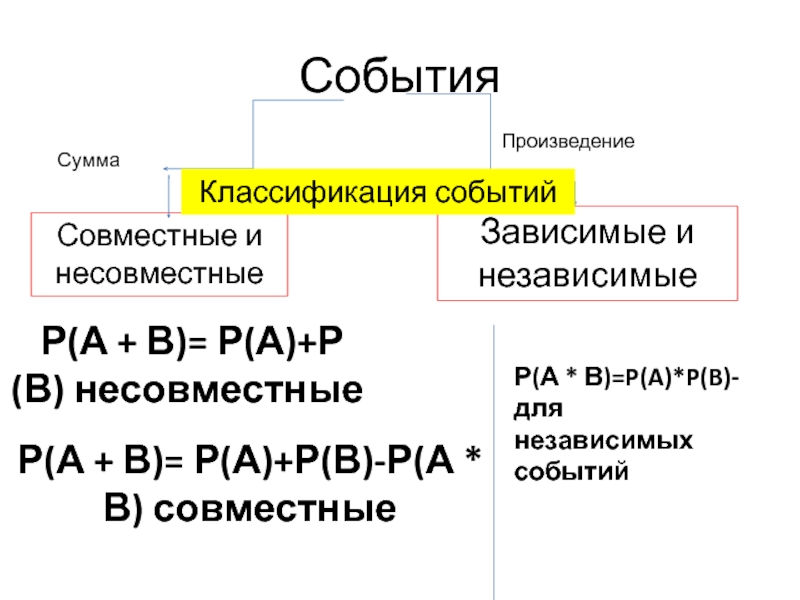
Слайд 16События
Совместные и несовместные
Зависимые и независимые
Сумма
Произведение
Классификация событий
Р(А + В)=
Р(А)+Р(В)-Р(А * В) совместные
Р(А + В)= Р(А)+Р(В) несовместные
Р(А * В)=P(A)*P(B)- для независимых событий
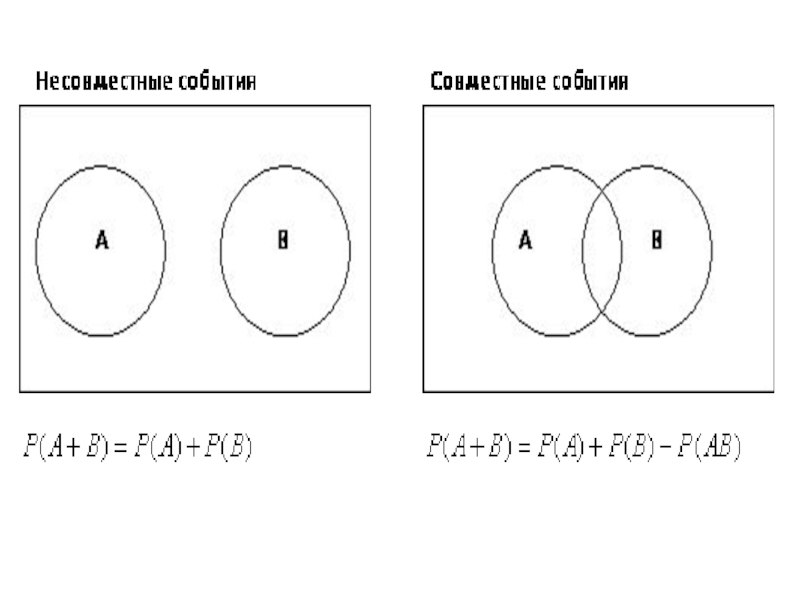
Слайд 17Несовместные события
Рассмотрим два случайных события A и B.
И определим третье
событие C
Тогда событие C можно трактовать как или появление события A или появление события B в ходе эксперимента.
Случайные события А и В называются несовместными, если при данном испытании (эксперименте) появление одного из них исключает появление другого события.
Пример :
Допустим, бросается игральный кубик и рассматриваются события
A - появление числа 2;
B - появление числа 5.
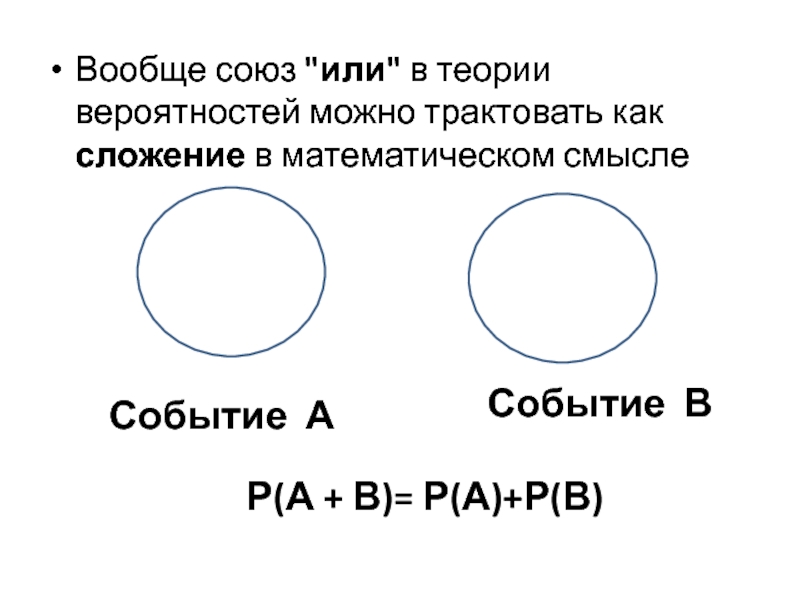
Слайд 18Вообще союз "или" в теории вероятностей можно трактовать как сложение в
математическом смысле
Событие А
Событие В
Р(А + В)= Р(А)+Р(В)
Вообще союз "или" в теории вероятностей можно трактовать как сложение в математическом смысле
Слайд 19
Бросаются два игральных кубика
A - появление числа 2;
B -
появление числа 5.
В этом случае событие A и B могут произойти одновременно в эксперименте, поэтому такие события называются совместные, т.е. и событие А и событие В
В этом случае событие A и B могут произойти одновременно в эксперименте, поэтому такие события называются совместные, т.е. и событие А и событие В
Совместные события
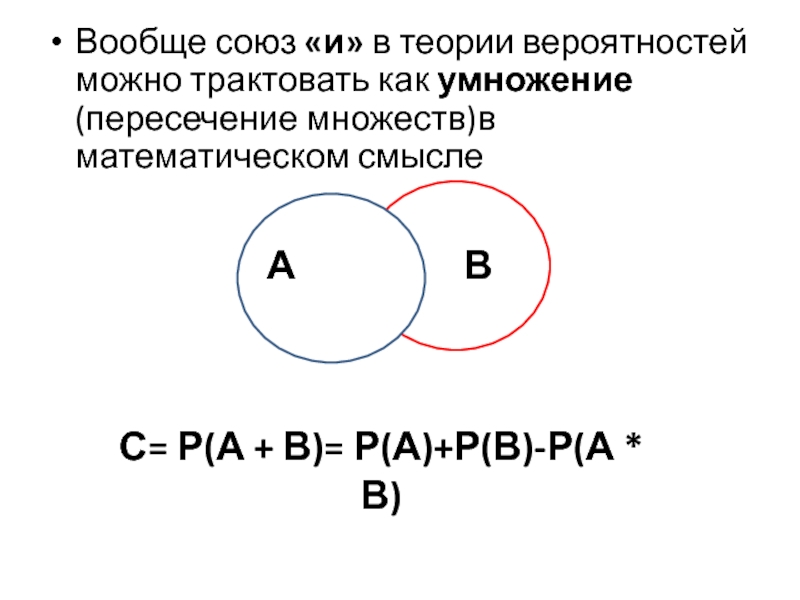
Слайд 20Вообще союз «и» в теории вероятностей можно трактовать как умножение (пересечение
множеств)в математическом смысле
А
В
С= Р(А + В)= Р(А)+Р(В)-Р(А * В)
Слайд 21Совместные события
Случайные события А и В называются совместными, если в проводимом эксперименте
эти события наступают одновременно.
Слайд 22Случайные события А и В называются независимыми, если появление одного из
них, например, А не изменяет (не влияет) вероятность появления другого события – В.
НЕЗАВИСИМЫЕ СОБЫТИЯ
Слайд 23В теории вероятностей события, появления которых не влияют на появления других
событий, в ходе проведения эксперимента, называются независимыми.
И для независимых событий вероятность
Р(А *В)=Р(А)*Р(В)
И для независимых событий вероятность
Р(А *В)=Р(А)*Р(В)
Слайд 24ПРИМЕР
Бросаются два игральных кубика и рассматриваются события:
A - выпадение числа 3
на 1-м кубике;
B - выпадение числа 2 на 2-м кубике.
Тогда событие С можно трактовать как одновременное выпадение числа 3 на первом кубике и числа 2 на втором.
B - выпадение числа 2 на 2-м кубике.
Тогда событие С можно трактовать как одновременное выпадение числа 3 на первом кубике и числа 2 на втором.
Слайд 25Какое число выпало на 1-м кубике никак не влияет на число,
которое выпадет на 2-м кубике, и наоборот.
Слайд 27Пример.
Допустим, имеется урна с 2 черными и 3 белыми шарами.
Шары последовательно вынимаются из урны (и не кладутся обратно в нее).
Выделим два события:
A - вынули белый шар;
B - вынули черный шар.
В этом случае событие интерпретируется так: сначала вынули белый шар, а затем черный.
Выделим два события:
A - вынули белый шар;
B - вынули черный шар.
В этом случае событие интерпретируется так: сначала вынули белый шар, а затем черный.
Слайд 28Случайные события А и В называются зависимыми, если появление одного из
них, например, А изменяет (влияет) вероятность появления другого события – В.
ЗАВИСИМЫЕ СОБЫТИЯ
Слайд 29Диагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения
между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру. Используется в математике, логике, менеджменте и других прикладных направлениях.
Слайд 32Два события называются противоположными, если в данном испытании они несовместны и одно из них
обязательно происходит.
Пример: ОРЕЛ-РЕШКА; Получил зачет - получил незачет; пришел в школу – не пришел в школу
Пример: ОРЕЛ-РЕШКА; Получил зачет - получил незачет; пришел в школу – не пришел в школу
ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ
Слайд 33На экзамене по геометрии школьник отвечает на один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по те»Параллелограмм», равна 0,15.
Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Слайд 34В магазине стоят два платёжных автомата. Каждый из них может быть
неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Слайд 35В торговом центре два одинаковых автомата продают кофе. Вероятность того, что
к концу дня в автомате закончится кофе равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12.
Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Слайд 36В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит
по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.
Слайд 37Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает
случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Слайд 38Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в
течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Слайд 39В магазине стоят два платёжных автомата. Каждый из них может быть
неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Слайд 40В торговом центре два одинаковых автомата продают кофе. Вероятность того, что
к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Слайд 41По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того,
что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Похожие презентации
Что такое shareslide.ru?
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Обратная связь
Email: Нажмите что бы посмотреть