СОШ Пономарева Наталья Николаевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике в 10 классе по теме Тригонометрические функции
Содержание
- 1. Презентация по математике в 10 классе по теме Тригонометрические функции
- 2. Цель: напомнить сведения о тригонометрических функциях, полученные
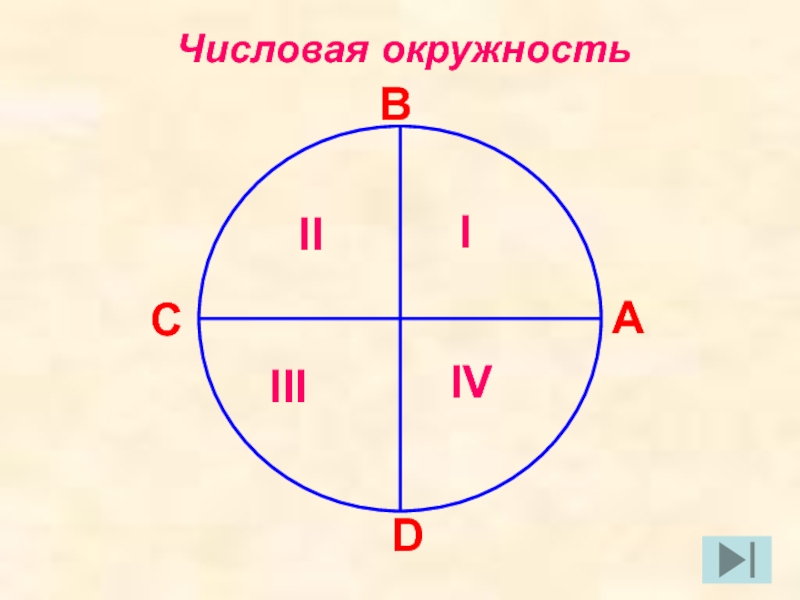
- 3. Числовая окружность
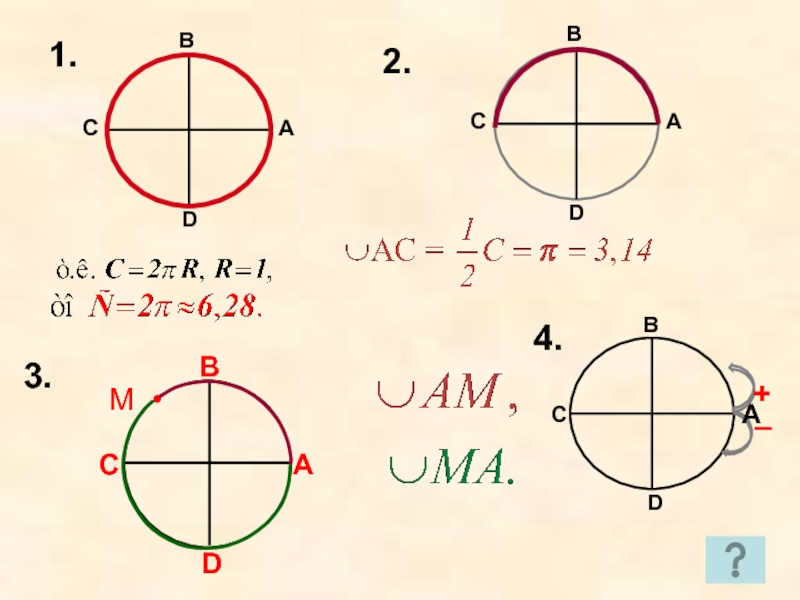
- 4. 1.2.М •3.ВСD4.А+–
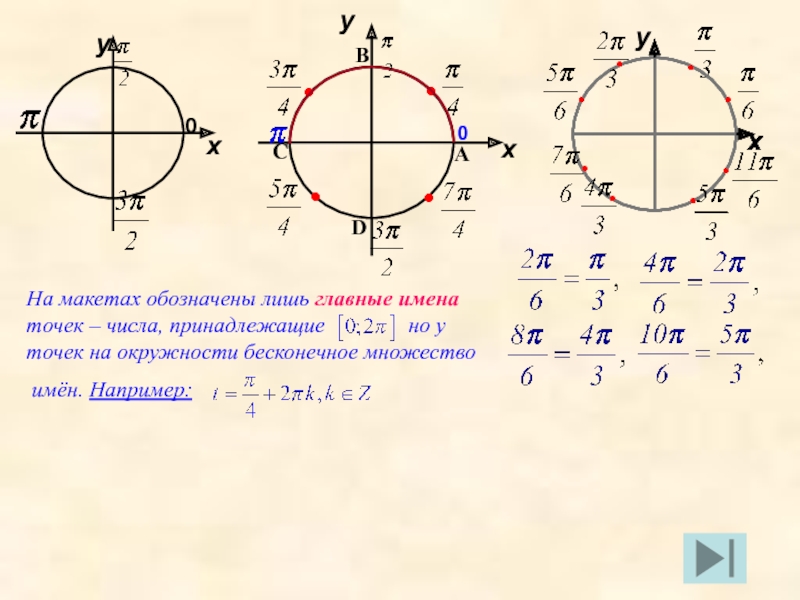
- 5. уАВСDНа макетах обозначены лишь главные имена точек
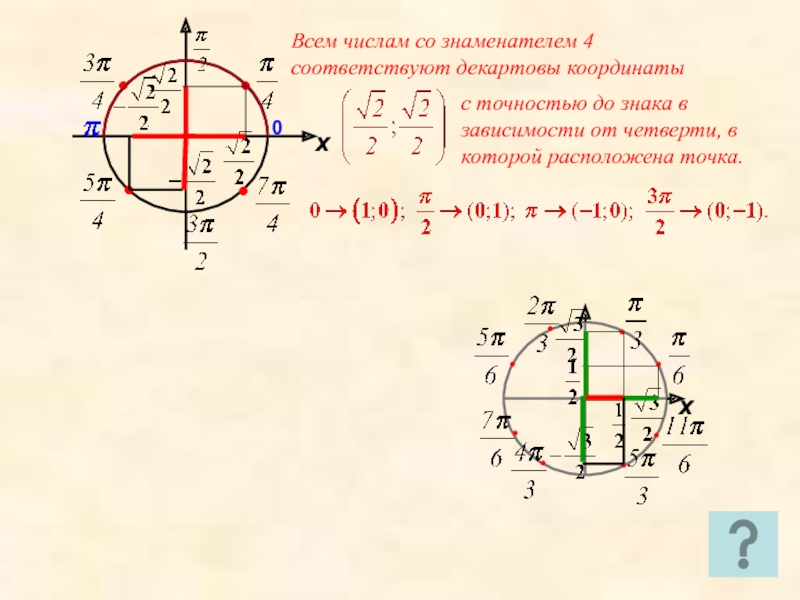
- 6. Всем числам со знаменателем 4 соответствуют декартовы
- 7. Синус, косинус, тангенс и котангенсЕсли M (t)
- 8. Свойства синуса, косинуса, тангенса и котангенса
- 9. Основные тригонометрические формулы
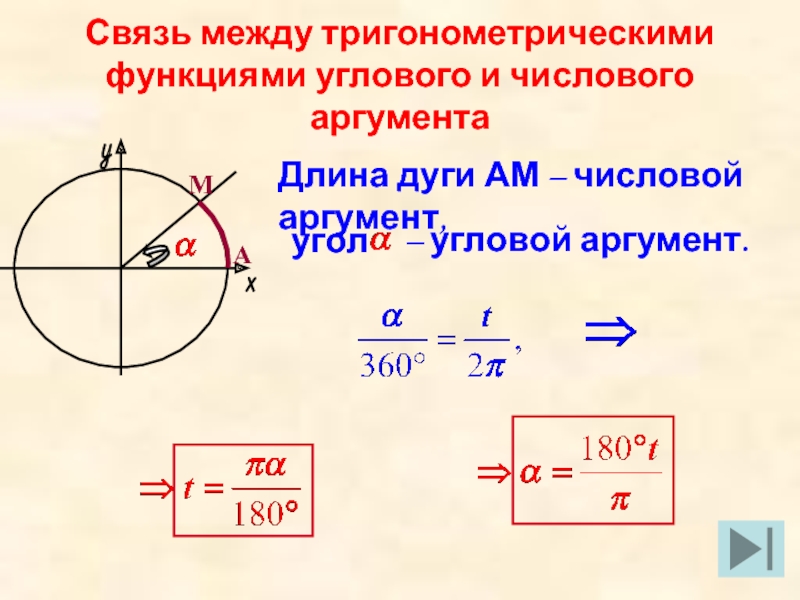
- 10. Связь между тригонометрическими функциями углового и числового аргументаАМДлина дуги АМ – числовой аргумент,угол – угловой аргумент.
- 11. Угол в 1 рад – это центральный
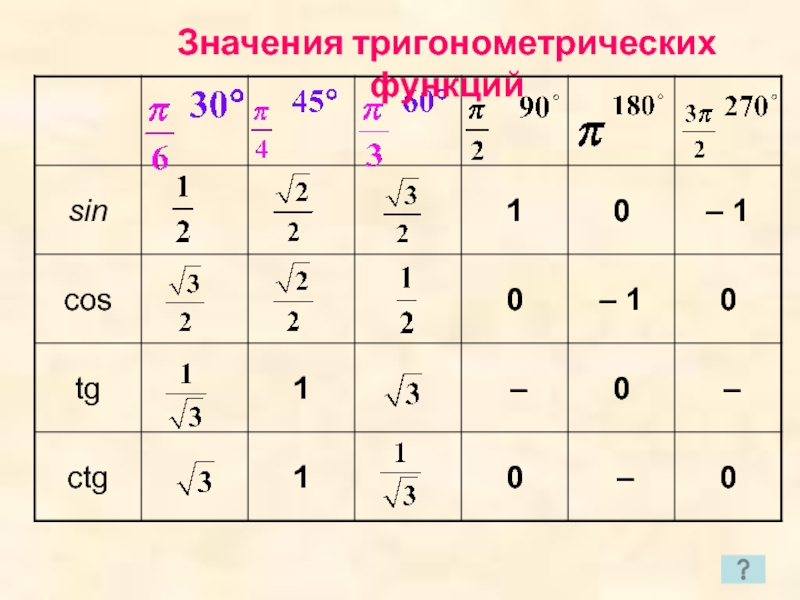
- 12. Значения тригонометрических функций
- 13. Тренировочные упражнения1.Точка М делит дугу АВ в
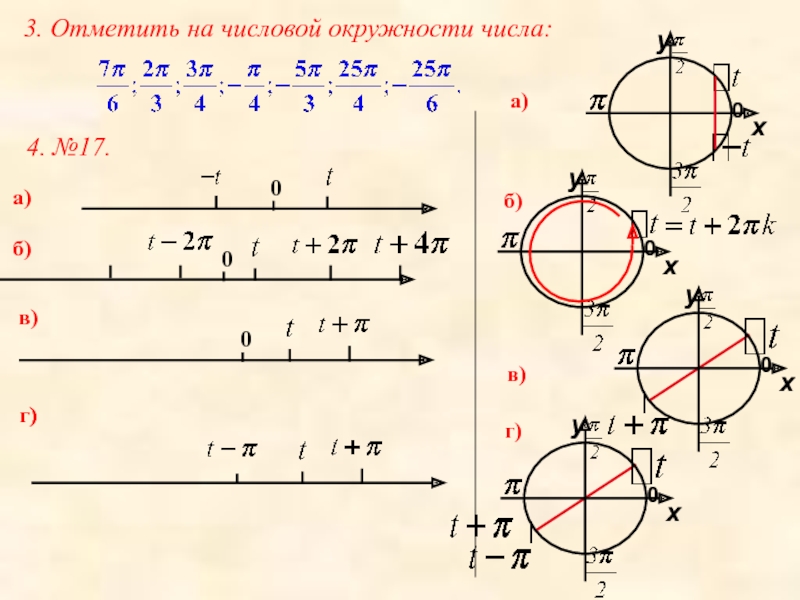
- 14. 3. Отметить на числовой окружности числа: 4. №17.а)б)в)г)а)б)в)г)г)
- 15. Итог урокаЧисловая окружность, радиус, четверти. Длина окружности.
Цель: напомнить сведения о тригонометрических функциях, полученные в 9 классе, подготовить к изучению новых сведений и свойств тригонометрических функций.
Слайд 1x = cost
Презентация на тему:
«Тригонометрические функции»
Подготовила учитель математики МКОУ Бондаревская
Слайд 2Цель: напомнить сведения о тригонометрических функциях, полученные в 9 классе, подготовить
к изучению новых сведений и свойств тригонометрических функций.
Слайд 5у
А
В
С
D
На макетах обозначены лишь главные имена точек – числа, принадлежащие
но у точек на окружности бесконечное множество
имён. Например:
имён. Например:
Слайд 6
Всем числам со знаменателем 4 соответствуют декартовы координаты
с точностью до знака
в зависимости от четверти, в которой расположена точка.
Слайд 7Синус, косинус, тангенс и котангенс
Если M (t) = M (x; y),
то
+
+
–
–
+
–
–
+
•
M(t)=M(x;y)
– 1
1
– 1
1
Знаки по четвертям:
+
–
+
–
Слайд 10Связь между тригонометрическими функциями углового и числового аргумента
А
М
Длина дуги АМ –
числовой аргумент,
угол
– угловой аргумент.
Слайд 11Угол в 1 рад – это центральный угол , длина дуги
которого равна радиусу окружности.
Таким образом, в тригонометрии независимую переменную мы можем считать числовым аргументом или угловым аргументом.
Слайд 13Тренировочные упражнения
1.
Точка М делит дугу АВ в отношении 2 : 3.
найти длину дуг: а) АМ; б) МВ; в) DM; г) МС
Решение: а) АМ =
2.
Точка Р делит третью четверть в отношении 1 : 5. Найдите длину дуги СР, РD, АР.
Ответ:
Слайд 15Итог урока
Числовая окружность, радиус, четверти. Длина окружности. Положительное и отрицательное направление
обхода.
Имена точек на числовой окружности. Какие декартовы координаты им соответствуют.
Определение синуса, косинуса, тангенса и котангенса. Знаки, значения.
Формулы, выражающие свойства тригонометрических функций.
Связь между тригонометрическими функциями числового и углового аргумента.
Таблица значений.
Имена точек на числовой окружности. Какие декартовы координаты им соответствуют.
Определение синуса, косинуса, тангенса и котангенса. Знаки, значения.
Формулы, выражающие свойства тригонометрических функций.
Связь между тригонометрическими функциями числового и углового аргумента.
Таблица значений.
Д/з. 1 – 7 № 12,15,16(в, г), 23, 24(а, г), 55.
§
