- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теория вероятности в ЕГЭ
Содержание
- 1. Презентация по математике Теория вероятности в ЕГЭ
- 2. Истинная логика нашего мира – правильный подсчет
- 3. Слайд 3
- 4. Какие из следующих событий – случайные, достоверные,
- 5. Слайд 5
- 6. m – число исходов, благоприятствующих событию n – число всех возможных исходов
- 7. Какова вероятность того, что из 5 цыплят один будет синего цвета?
- 8. Кубики1. Подбрасывают два игральных кубика. Какова вероятность
- 9. Монеты1. Перед началом футбольного матча судья бросает
- 10. Деление на группы1. Конкурс исполнителей проводится в
- 11. Производство
- 12. 1. В квадрат со стороной, равной 1,
- 13. Деление на группы3. В классе учится 21
- 14. Слайд 14
- 15. Слайд 15
- 16. ЗадачаОтвет: 7.
- 17. Независимые событияСобытие B называют независимым от
- 18. Вероятность произведения двух независимых событий равна
- 19. 3. Перед началом волейбольного матча капитаны команд
- 20. Производство4. Номера российских автомобилей состоят из записанных
- 21. Решение:Сначала обозначим путь (или пути), которым паук
- 22. 1. Найти вероятность поражения цели при совместной
- 23. Слайд 23
- 24. Производство3. При изготовлении подшипников диаметром 67 мм
- 25. Виды случайных событий События называются несовместными, если
- 26. Вероятность суммы двух несовместных событий равна
- 27. Решение: Джон попадает в муху, если схватит
- 28. Разные задачи5. Из районного центра в деревню
- 29. Производство6. Всем пациентам с подозрением на гепатит
- 30. 3. При артиллерийской стрельбе автоматическая система делает
- 31. Спасибо за внимание!
Слайд 2Истинная логика нашего мира – правильный подсчет вероятностей.
(Джеймс Максвелл)
Теория вероятностей
это раздел математики, изучающий вероятно-статистические закономерности
Слайд 4Какие из следующих событий – случайные, достоверные, невозможные:
черепаха научиться говорит;
ваш день рождения – 19 октября
день рождение вашего друга – 30 февраля;
вы выиграете участвуя в лотереи;
вы не выигрываете, участвуя в беспроигрышной лотереи;
вы проиграете партию в шахматы;
на следующей недели испортиться погода;
вы нажали на звонок, а он не зазвонил;
после четверга будет пятница;
после пятницы будет воскресенье.
Слайд 8Кубики
1. Подбрасывают два игральных кубика. Какова вероятность того, что в сумме
Рассмотрим событие А, которое означает, что в сумме выпадет 6 очков.
Количество равновозможных
исходов – 36.
Количество благоприятных
исходов – 5.
Р(А) =
Слайд 9Монеты
1. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая
Решение. Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Слайд 10Деление на группы
1. Конкурс исполнителей проводится в 5 дней. Всего заявлено
Решение.
На третий день запланировано выступлений.
Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
Слайд 121. В квадрат со стороной, равной 1, бросают случайную точку.
Какова вероятность того, что расстояние от этой точки до
ближайшей стороны квадрата не превосходит 0,25?
Решение.
Площадь всего квадрата равна 1.
Множество точек, расстояние от которых до ближайшей его стороны не превосходит 0,25 – это закрашенная на рисунке часть квадрата (внутри данного квадрата расположен квадрат со стороной, равной 0,5).
Площадь этой части равна 1-0,5² =0,75.
Отсюда вероятность равна Р(А)= 0,75/1=0,75 Ответ: 0,75
Разные задачи
Слайд 13Деление на группы
3. В классе учится 21 человек. Среди них две
Решение.
Пусть Аня оказалась в некоторой группе.
Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности.
Вероятность этого события равна 2 : 20 = 0,1.
Слайд 17Независимые события
Событие B называют независимым от события A, если появление
Пример 1. При бросании кубика вероятность появления числа 2 при втором бросании не зависит от результатов первого бросания.
Пример 2. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Слайд 18 Вероятность произведения двух независимых событий равна произведению вероятностей этих событий P(AВ) =
Теорема произведения вероятностей
Слайд 193. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы
Решение. Начинает игру – О, не начинает - Р
Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру.
О Р О
Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим:
0,5·0,5·0,5 = 0,125.
Монеты
Слайд 20Производство
4. Номера российских автомобилей состоят из записанных последовательно одной буквы, трех
Решение.
Количество всех исходов: 12 ∙ 10 ∙ 10 ∙ 10 ∙ 12 ∙ 12
А: «Все цифры и все буквы в номере автомобиля будут разными»
Количество благоприятных исходов: 12 ∙ 10 ∙ 9 ∙ 8 ∙ 11 ∙ 10
Р(А) =
.
Ответ:
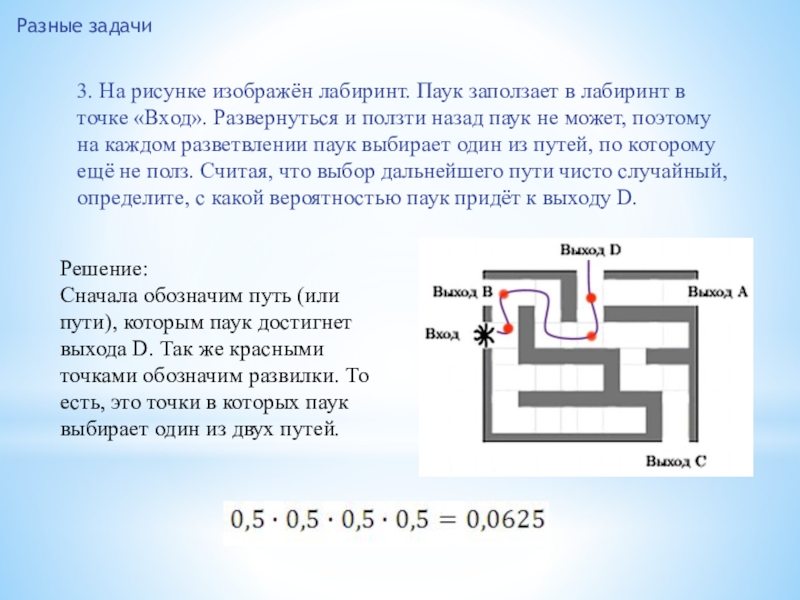
Слайд 21Решение:
Сначала обозначим путь (или пути), которым паук достигнет выхода D. Так
Разные задачи
3. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Слайд 221. Найти вероятность поражения цели при совместной стрельбе тремя орудиями, если
Решение. Поскольку события А, В И С являются независимыми, то искомая вероятность вычисляется, согласно формуле
Выстрелы
Слайд 24Производство
3. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр
Решение.
По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Слайд 25Виды случайных событий
События называются несовместными, если появление одного из них
Пример
несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное;
совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное.
Слайд 26 Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий P(A+В) =
Теорема сложения вероятностей
Слайд 27Решение:
Джон попадает в муху, если схватит пристрелянный револьвер и попадет
или если схватит не пристрелянный револьвер и попадает из него 0,6·0,2 = 0,12
Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий:
0,36 + 0,12 = 0,48.
Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна
1 − 0,48 = 0,52.
2. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Выстрелы
Слайд 28Разные задачи
5. Из районного центра в деревню ежедневно ходит автобус. Вероятность
Решение.
Рассмотрим события A = «в автобусе меньше 15 пассажиров»
и В = «в автобусе от 15 до 19 пассажиров».
Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем:
0,94 = 0,56 + P(В), откуда
P(В) = 0,94 − 0,56 = 0,38.
Слайд 29Производство
6. Всем пациентам с подозрением на гепатит делают анализ крови. Если
Решение.
Анализ пациента может быть положительным по двум причинам:
А) пациент болеет гепатитом, его анализ верен;
B) пациент не болеет гепатитом, его анализ ложен.
Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:
Слайд 303. При артиллерийской стрельбе автоматическая система делает выстрел по цели, вероятность
Выстрелы