- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теория вероятности для решения задачи ЕГЭ
Содержание
- 1. Презентация по математике Теория вероятности для решения задачи ЕГЭ
- 2. Слайд 2
- 3. Теоремы сложения и умножения.Теорема сложения вероятностей несовместных
- 4. Теорема умножения вероятностей независимых событий. Вероятность совместного
- 5. Вероятность наступления события A, вычисленная в предположении,
- 6. 1.На экзамене по геометрии школьнику достаётся один
- 7. 2. В торговом центре два одинаковых автомата
- 8. 3. В магазине стоят два платёжных автомата.
- 9. 4. Помещение освещается фонарём с двумя лампами.
- 10. 5. Если гроссмейстер А. играет белыми, то
- 11. 6. Биатлонист пять раз стреляет по мишеням.
- 12. 7. В классе 26 человек, среди
- 13. 8. На фабрике керамической посуды 10% произведённых
- 14. 9. В магазине три продавца. Каждый из
- 15. 10. По отзывам покупателей Иван Иванович оценил
- 16. 11. Вероятность того, что батарейка бракованная, равна
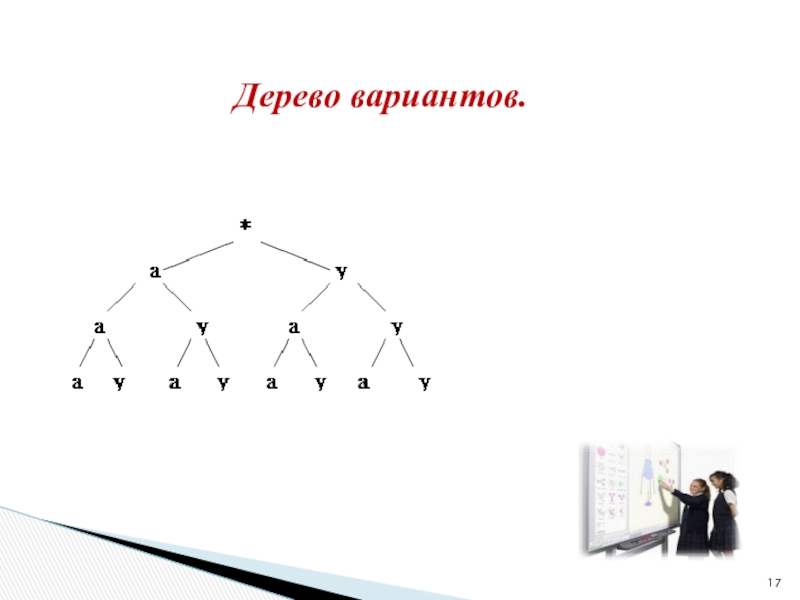
- 17. Дерево вариантов.
- 18. 1. Две фабрики выпускают одинаковые стекла для
- 19. 2. Агрофирма закупает куриные яйца в двух
- 20. 3. Ковбой Джон попадает в муху на
- 21. 4. Автоматическая линия изготавливает батарейки. Вероятность того,
- 22. 5. Всем пациентам с подозрением на гепатит
- 23. Всем пациентам с подозрением на гепатит делают
- 24. Анализ дает положительный результат в случаях
- 25. 6.На рисунке изображён лабиринт. Паук заползает в
- 26. Неравенства.1.Вероятность того, что новый электрический чайник прослужит
- 27. 2.Вероятность того, что на тесте по биологии
- 28. 3. При изготовлении подшипников диаметром 67 мм
- 29. 4.Из районного центра в деревню ежедневно ходит
Слайд 3Теоремы сложения и умножения.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из
безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B); P( + +…+ =P( +P +…+P( ).
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме
вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B)-P(AB)
Слайд 4Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна
P(AB)=P(A)•P(B)
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий
равна произведению одного из них на условную вероятность второго:
P(AB)=P(A)• (B)=P(B)• (A)
Слайд 5Вероятность наступления события A, вычисленная в предположении,
что событие B уже
события A при условии B и обозначается (A) или P(A/B). Если A и B – независимые события, то P(B)- (B)= (B).
Слайд 61.На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных
Решение
Р=0,2+0,15=0,25
Слайд 72. В торговом центре два одинаковых автомата продают кофе.
Вероятность того,
Вероятность того, что кофе закончится в обоих автоматах, равна 0,12.
Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение
А – кофе закончится в 1м автомате
В - кофе закончится во 2м автомате
Р(А)=Р(В)=0,3
кофе закончится в обоих автоматах
- кофе закончится хотя бы в одном
Но противоположное событие
означает – кофе останется в обоих автоматах
Слайд 83. В магазине стоят два платёжных автомата. Каждый из них может
Решение
- автомат неисправен
- автомат исправен
Слайд 94. Помещение освещается фонарём с двумя лампами. Вероятность
перегорания одной лампы
Решение
Слайд 105. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера
Решение
Если А играет чёрными, то потом белыми.
Р=0,52*0,3=0,156
Слайд 116. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень
Решение
Независимые события
Слайд 12 7. В классе 26 человек, среди них два близнеца —
Решение
Р1(попадание в первую группу одного из близнецов) =
Р2(попадание в первую группу второго из близнецов) =
Р(обоих)=
Так как групп две, то
Слайд 138. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При
Решение
10% брака – это 0,1 с браком и 0,9 – без брака
ОТК обнаруживает 80% от бракованных, это
В продажу поступило 1-0,08=0,92 всех произведённых тарелок,
из них 0,9 – без брака
Слайд 149. В магазине три продавца. Каждый из них занят с клиентом
Решение
Слайд 1510. По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность
Решение
Слайд 1611. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине
Решение
Слайд 181. Две фабрики выпускают одинаковые стекла для автомобильных фар.
Первая фабрика
Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите
вероятность того, что случайно купленное в магазине
стекло окажется бракованным.
.
Слайд 192. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц
Слайд 203. Ковбой Джон попадает в муху на стене с вероятностью 0,9,
из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Слайд 214. Автоматическая линия изготавливает батарейки. Вероятность того,
что готовая батарейка неисправна,
батарейка проходит систему контроля. Вероятность того, что система
забракует неисправную батарейку, равна 0,99. Вероятность того, что система
по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность
того, что случайно выбранная из упаковки батарейка будет забракована.
Слайд 225. Всем пациентам с подозрением на гепатит делают анализ крови. Если
Слайд 23Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ
Пусть – вероятность того, что пациент, поступивший с подозрением на гепатит, действительно болен гепатитом.
Тогда – вероятность того, что пациент, поступивший с подозрением на гепатит, не болен гепатитом.
Слайд 24Анализ дает положительный результат в случаях
или (сложение)
пациент не болен и анализ ложно положителен
Так как по условию задачи у 6% пациентов с подозрением на гепатит анализ дает положительный результат, то
р*0,9+(1-р)*0,01=0,06
0,9р-0,01р=0,05
0,89р=0,05
Р=5/89
Р=0,05617
Округляем до тысячных: р=0,056 .
Ответ: 0,056.
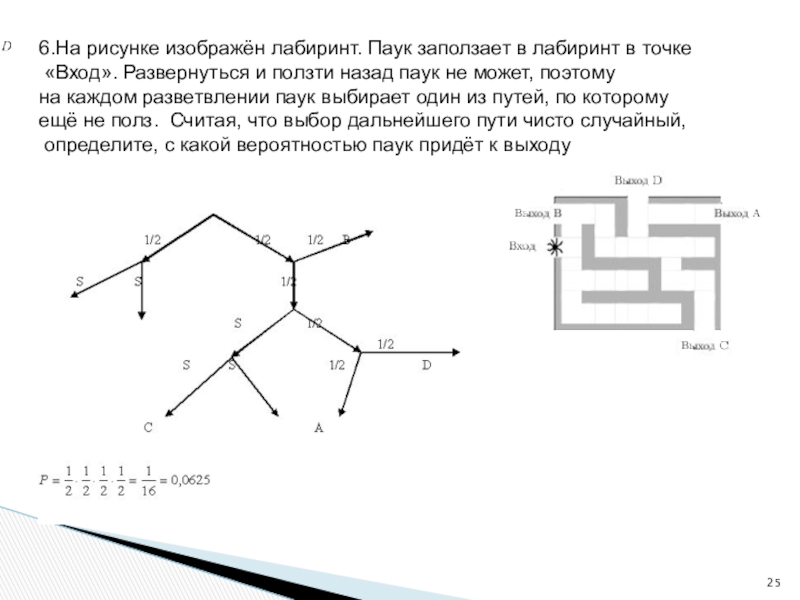
Слайд 256.На рисунке изображён лабиринт. Паук заползает в лабиринт в точке
«Вход».
на каждом разветвлении паук выбирает один из путей, по которому
ещё не полз. Считая, что выбор дальнейшего пути чисто случайный,
определите, с какой вероятностью паук придёт к выходу
.
Слайд 26Неравенства.
1.Вероятность того, что новый электрический чайник прослужит больше года,
равна 0,97.
Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Слайд 272.Вероятность того, что на тесте по биологии учащийся О. верно решит
10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11
задач.
P(x>11)=0.67
P(x>10)=0.74
P(x=11) - ?
(x>10)=(x=11)+(x>11)
0.74=P(x=11)+0.67
P(x=11)=0.07
Другой способ рассуждений.
Больше 10: 11ю, 12ю,….. Р1=0,74
Больше 11:12ю, 13ю,… Р2=0,67
Ровно 11: Р=Р1-Р2=0,74-0,67=0,07
Слайд 283. При изготовлении подшипников диаметром 67 мм вероятность того, что
диаметр
Найдите вероятность того, что случайный подшипник будет иметь диаметр
меньше чем 66,99 мм или больше чем 67,01 мм.
Слайд 294.Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что
Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите
вероятность того, что число пассажиров будет от 15 до 19.