- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теория вероятностей
Содержание
- 1. Презентация по математике Теория вероятностей
- 2. «Вероятность математическая – это числовая характеристика степени
- 3. Исходом эксперимента называют значение наблюдаемого признака, непосредственно
- 4. События бывают детерминированные (солнце встает), и случайные
- 5. Под испытанием (опытом) в теории вероятностей принято понимать наблюдение
- 6. Вероятность - отношение числа благоприятствующих исходов, к
- 7. Частота события – сколько раз оно выпало
- 8. Достоверным называют событие, которое в результате испытание
- 9. Случайные события называются несовместными если появление одного исключает
- 10. Противоположными называют события такие, что наступление события
- 11. Случайная величина Х – однозначная действительная функция,
- 12. Охарактеризуйте событие, о котором идет речь, как
- 13. Укажите, какие из описанных пар событий являются
- 14. Из событий 1) «Идет дождь, 2) «на
- 15. Тетраэдр одна грань серая, три другие белые.
- 16. Назовите событие, противоположное указанному в данном испытании:При
- 17. Допустим, что 5 раз подбрасывалась монеты и
- 18. Ученик записал в тетради произвольное трехзначное число.
- 19. Бросают 2 монеты, какова вероятность того, что выпадет хотя бы один орел? (2 решения)Задача 8
- 20. В некоторой настольной игре игрок бросает сразу
- 21. На карточках записаны цифра 1,2,34. Карточки перевернули
- 22. Из 4 шаров, занумерованных числами 1,2,3 и
- 23. В коробке «Ассорти» - 20 неразличимых по
- 24. В вазе 11 гвоздик, из которых 4
- 25. Случайно нажимают три клавиши одной октавы. Найдите
- 26. Найдите вероятность того, что случайно выбранная точка
- 27. Схема Бернулли предполагает, что один и тот
- 28. Какова вероятность того, что при четырех бросаниях
«Вероятность математическая – это числовая характеристика степени возможности появления какого либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях» А.Н. Колмогоров
Слайд 2«Вероятность математическая – это числовая характеристика степени возможности появления какого либо
определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях» А.Н. Колмогоров
Слайд 3Исходом эксперимента называют значение наблюдаемого признака, непосредственно полученное по окончании эксперимента.
Каждый раз эксперимент заканчивается одним и только одним исходом.
Событием, наблюдаемым в эксперимента, называют появление исхода, обладающего заранее указанным свойством.
В конкретном эксперименте может являться не любые события, а только такие, которые могут быть определены через свойства исходов этого эксперимента.
Слайд 4События бывают детерминированные (солнце встает), и случайные те, которые происходят не
при каждом проведении опыта, одни случаются чаще другие реже.
Слайд 5Под испытанием (опытом) в теории вероятностей принято понимать наблюдение какого-либо явления при соблюдении
определенного комплекса условий, который должен каждый раз строго выполняться при повторении данного испытания. Если то же самое явление наблюдается при другом комплексе условий, то это уже другое испытание.
Слайд 6Вероятность - отношение числа благоприятствующих исходов, к общему числу равновозможных исходов
(классическое).
Вероятность - предел относительной частоты при неограниченном числе испытания (статистическое).
Вероятность - отношение длин, площадей или объемом двух областей: общей, в которой лежат все возможные исходы и благоприятствующей, в которой лежат интересующие нас исходы
Слайд 7Частота события – сколько раз оно выпало в ходе испытаний.
Относительная частота
– это отношение числа испытаний в которых событие наступило к общему числу испытаний.
Слайд 8Достоверным называют событие, которое в результате испытание должно произойти.
Невозможным называют событие
которое в результате испытания произойти не может.
События называются равновозможными если в результате испытания не одно из них не является объективно более возможным.
Слайд 9Случайные события называются несовместными если появление одного исключает появление другого. В противном
случае они называются совместными.
Теорема сложения вероятностей. Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий:
Р(A+B)=Р(А)+Р(В)- Р(AB)
Теорема сложения вероятностей. Вероятность объединения произвольных событий равна сумме их вероятностей за вычетом вероятности произведения событий:
Р(A+B)=Р(А)+Р(В)- Р(AB)
Слайд 10Противоположными называют события такие, что наступление события А означает не наступление
В и наоборот.
Независимыми называются такие события, что наступление одного из них не зависит от наступления другого.
Если событие С означает совместное наступление двух независимых событий А и В, то вероятность С равна произведению вероятностей А и В.
Р(С)=Р(А)*Р(В)
Слайд 11Случайная величина Х – однозначная действительная функция, определенная на множестве всех
возможных исходов эксперимента: Х=Х(ω).
Ряд распределения случайной величины
Слайд 12Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное.
Оцените его словами «стопроцентная вероятность», «нулевая вероятность», «маловероятно», «достаточно вероятно»:
а) рождение моего друга – число, меньше чем 32;
б) на уроке математики ученики делали физические упражнения;
в) на уроке математики ученики решали математические задачи;
г) из интервала (1;2) наугад взяли число, оно оказалось натуральным;
д) вверх подкинули монету она упала на землю «орлом»;
е) вверх подкинули монету и она упала на землю, встав на ребро.
а) рождение моего друга – число, меньше чем 32;
б) на уроке математики ученики делали физические упражнения;
в) на уроке математики ученики решали математические задачи;
г) из интервала (1;2) наугад взяли число, оно оказалось натуральным;
д) вверх подкинули монету она упала на землю «орлом»;
е) вверх подкинули монету и она упала на землю, встав на ребро.
Задача 1
Слайд 13Укажите, какие из описанных пар событий являются совместными, а какие несовместными.
В сыгранное Катей и Славой партии в шахматы:
Катя выиграла, Слава проиграл.
Катя проиграла, Слава проиграл.
Катя выиграла, Слава проиграл.
Катя проиграла, Слава проиграл.
Задача 2
Слайд 14Из событий 1) «Идет дождь, 2) «на небе нет ни облачка»
3) «Наступило лето» - составить всевозможные пары выявить среди них пары совместных и несовместных событий.
Задача 3
Слайд 15Тетраэдр одна грань серая, три другие белые. Тетраэдр бросают на стол
и наблюдают за гранью, которой он соприкасается со столом. Являются ли равновозможными события «тетраэдр упал на серую грань» и «тетраэдр упал на белую грань»?
Задача 4
Слайд 16Назовите событие, противоположное указанному в данном испытании:
При бросании монеты упала решка;
При
бросании игральной кости выпало 5 очков;
При бросании игральной кости выпало четное число очков;
Алеша вытащил выигрышный билет в розыгрыше лотереи.
При бросании игральной кости выпало четное число очков;
Алеша вытащил выигрышный билет в розыгрыше лотереи.
Задача 5
Слайд 17Допустим, что 5 раз подбрасывалась монеты и каждый раз выпал орел.
Какова вероятность того, что при новом броске выпадет орел ?
Задача 6
Слайд 18Ученик записал в тетради произвольное трехзначное число. Какова вероятность, что это
число при делении на 11 дает в остатке 7.
Задача 7
Слайд 19Бросают 2 монеты, какова вероятность того, что выпадет хотя бы один
орел? (2 решения)
Задача 8
Слайд 20В некоторой настольной игре игрок бросает сразу два кубика и делает
столько ходов, какова сумма выпавших очков. Какова вероятность, что игрок сделает менее 10 ходов?
Задача 9
Слайд 21На карточках записаны цифра 1,2,34. Карточки перевернули и перемешали. Затем открыли
наугад последовательно одну за другой, расположив их в ряд слева направо. Какова вероятность того, что в результате получилось число 123.
Задача 10
Слайд 22Из 4 шаров, занумерованных числами 1,2,3 и 4 наугад вынимают два
шара. Какова вероятность того, что вынутые шары имеют номера 2 и 3.
Задача 11
Слайд 23В коробке «Ассорти» - 20 неразличимых по виду конфет, из которых
12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять 2 конфеты. Какова вероятность, что:
А) обе конфеты с шоколадной начинкой;
Б) конфеты с разными начинками.
А) обе конфеты с шоколадной начинкой;
Б) конфеты с разными начинками.
Задача 12
Слайд 24В вазе 11 гвоздик, из которых 4 красные. В темноте наугад
вынимают три гвоздики. Какова вероятность того, что хотя бы одна из них будет красной? (Противоположное)
Задача 13
Слайд 25Случайно нажимают три клавиши одной октавы. Найдите вероятность того, что:
А) звучат
ноты си и до;
Б) звучит нота ля;
Б) звучит нота ля;
Задача 14
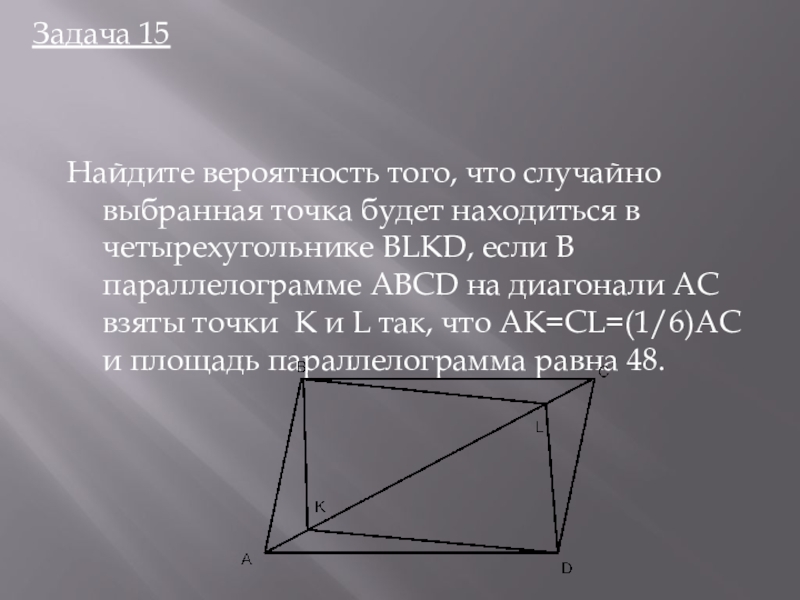
Слайд 26Найдите вероятность того, что случайно выбранная точка будет находиться в четырехугольнике
BLKD, если В параллелограмме ABCD на диагонали AC взяты точки K и L так, что AK=CL=(1/6)AC и площадь параллелограмма равна 48.
Задача 15
Слайд 27Схема Бернулли предполагает, что один и тот же эксперимент повторяется в
неизменных условиях независимо, n раз; мы наблюдаем за появлением (успех) или непоявлением (неудача) в каждом эксперименте одного и того же события А, вероятность появление данного события в каждом испытании постоянна и равна p. Подсчитываем сколько k «успехов». Тогда вероятность наступления k успехов из n равна:
Слайд 28Какова вероятность того, что при четырех бросаниях игрального кубика «тройка» выпадет:
А) ровно 2 раза;
Б) ровно 3 раза.
Задача 16
