Долинска Сахалинской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Решение неравенств методом интервалов
Содержание
- 1. Презентация по математике Решение неравенств методом интервалов
- 2. Содержание Пример 1.Пример 2.Пример 3.
- 3. Пример 1. Решить неравенство: (х - 2)(х
- 4. 2-6х1). (х - 2)(х + 6) =
- 5. Пример 2. Решить неравенство: 2х2 - 3х
- 6. +10,5х1). 2х2 - 3х + 1 =
- 7. Пример 3. Решить неравенство: -х2 + х
- 8. +–4-3х1). -х2 + х + 12 =
Содержание Пример 1.Пример 2.Пример 3.
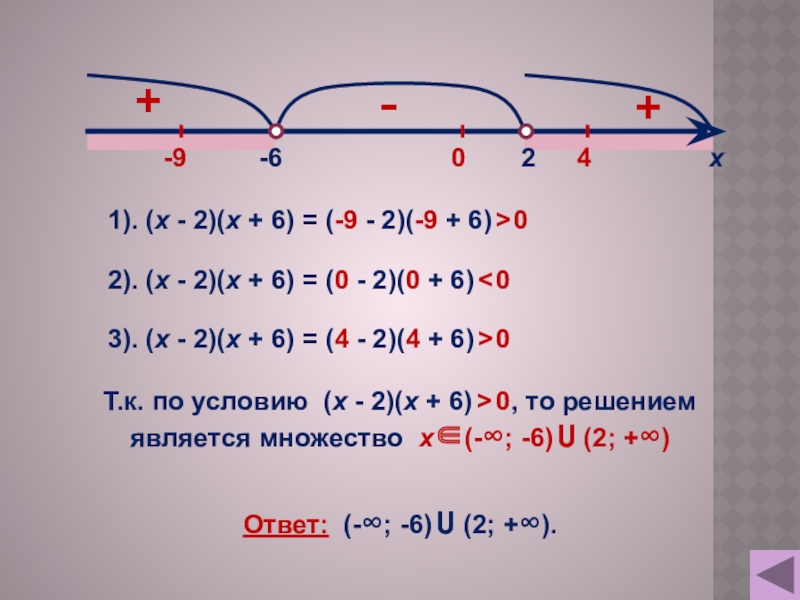
Слайд 3Пример 1. Решить неравенство: (х - 2)(х + 6) > 0
Найдём
корни квадратного трехчлена из уравнения:
(х – 2)(х + 6) = 0
(х – 2)(х + 6) = 0
х1 = 2; х2 = -6
Отметим эти корни на числовой прямой:
2
-6
х
Получим три промежутка:
Определим знаки (х - 2)(х + 6) на каждом из полученных промежутков:
х – 2 = 0 или х + 6 = 0
Слайд 42
-6
х
1). (х - 2)(х + 6) = (-9 - 2)(-9 +
6) > 0
-9
2). (х - 2)(х + 6) = (0 - 2)(0 + 6) < 0
0
4
3). (х - 2)(х + 6) = (4 - 2)(4 + 6) > 0
+
+
–
Т.к. по условию (х - 2)(х + 6) > 0, то решением
является множество х(-∞; -6) U (2; +∞)
Ответ: (-∞; -6) U (2; +∞).
Слайд 5Пример 2. Решить неравенство: 2х2 - 3х + 1 < 0
Найдём
корни квадратного трехчлена из уравнения:
2х2 - 3х + 1 = 0
2х2 - 3х + 1 = 0
х1 = 1; х2 = 0,5
Отметим эти корни на числовой прямой:
1
0,5
х
Получим три промежутка:
Определим знаки 2х2 - 3х + 1 на каждом из полученных промежутков:
Слайд 6+
1
0,5
х
1). 2х2 - 3х + 1 = 2∙02 - 3∙0 +
1 > 0
0
0,8
1,2
+
–
Т.к. по условию 2х2 - 3х + 1 < 0, то решением
является множество х(0,5; 1)
Ответ: (0,5; 1).
2). 2х2 - 3х + 1 = 2∙0,82 - 3∙0,8 + 1 < 0
3). 2х2 - 3х + 1 = 2∙1,22 - 3∙1,2 + 1 > 0
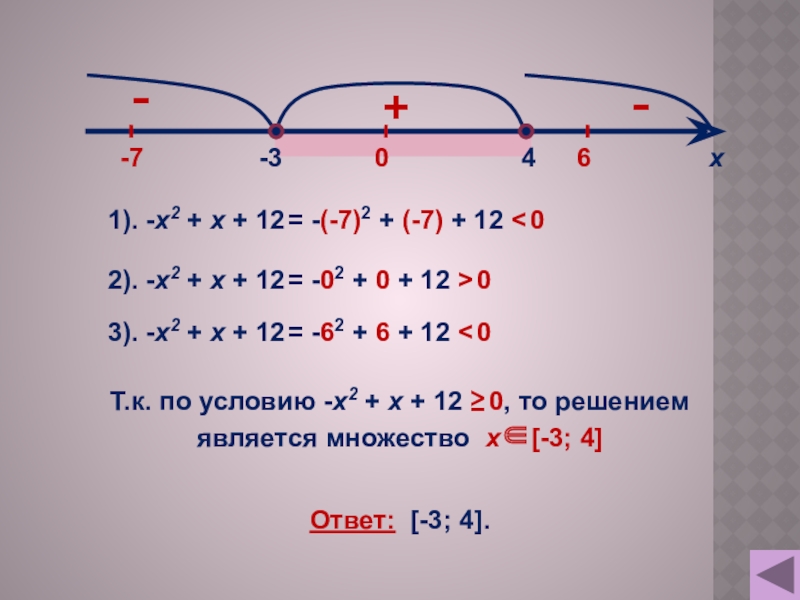
Слайд 7Пример 3. Решить неравенство: -х2 + х + 12 ≥ 0
Найдём
корни квадратного трехчлена из уравнения:
-х2 + х + 12 = 0
-х2 + х + 12 = 0
х1 = 4; х2 = -3
Отметим эти корни на числовой прямой:
4
-3
х
Получим три промежутка:
Определим знаки -х2 + х + 12 на каждом из полученных промежутков:
Слайд 8+
–
4
-3
х
1). -х2 + х + 12 = -(-7)2 + (-7) +
12 < 0
-7
0
6
–
Т.к. по условию -х2 + х + 12 ≥ 0, то решением
является множество х[-3; 4]
Ответ: [-3; 4].
2). -х2 + х + 12 = -02 + 0 + 12 > 0
3). -х2 + х + 12 = -62 + 6 + 12 < 0
