Бутенко Е.С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике при подготовки к ЕГЭ
Содержание
- 1. Презентация по математике при подготовки к ЕГЭ
- 2. Слайд 2
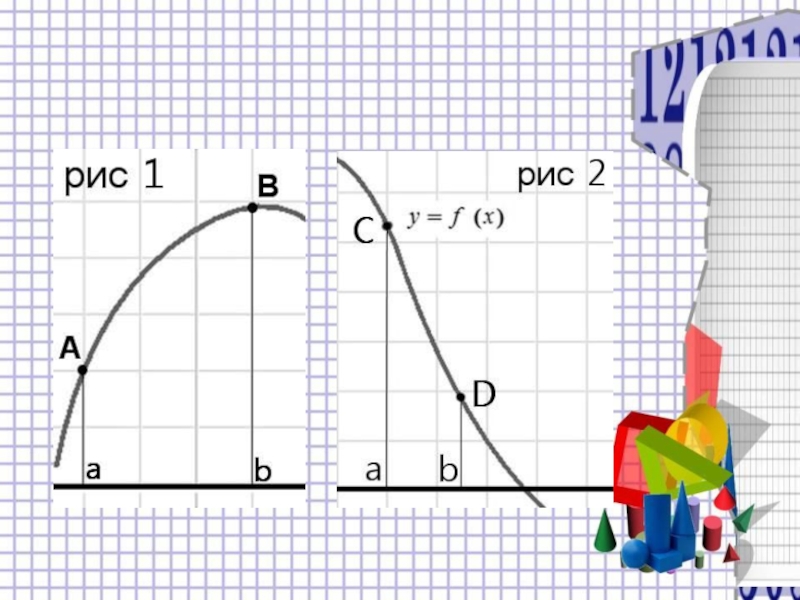
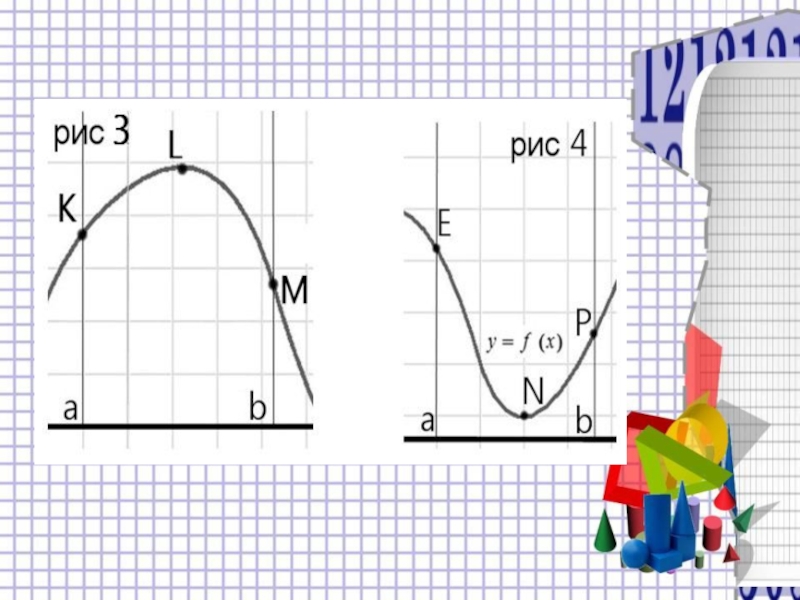
- 3. Задачи на нахождение точек экстремума функции.Алгоритм нахождения
- 4. Вывод:если в точке производная меняет знак с
- 5. Задание 12.Найдите точку минимума функции
- 6. Слайд 6
- 7. Слайд 7
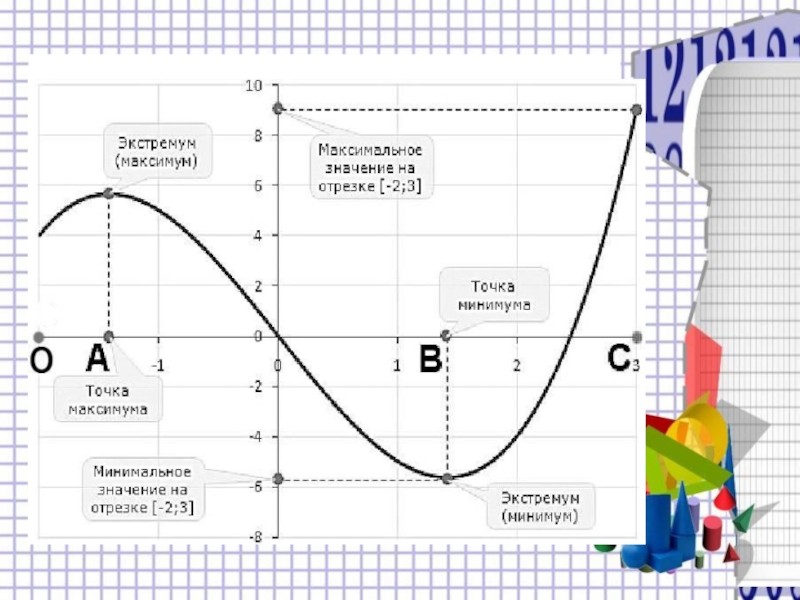
- 8. Задачи на наибольшее и наименьшее значение функции
- 9. Задание 12. 1. Найдите наибольшее значение функции y = x3 +
- 10. Не робей, не бойся ты заданий И
Задачи на нахождение точек экстремума функции.Алгоритм нахождения точек экстремума.1. Находим производную функции2. Находим нули производной путём приравнивания производной к нулю, решаем полученное уравнение3. Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах,
Слайд 3Задачи на нахождение точек
экстремума функции.
Алгоритм нахождения точек экстремума.
1. Находим производную
функции
2. Находим нули производной путём приравнивания производной к нулю, решаем полученное уравнение
3. Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах, путём подстановки значений из интервалов в выражение производной
4. Делаем вывод
2. Находим нули производной путём приравнивания производной к нулю, решаем полученное уравнение
3. Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах, путём подстановки значений из интервалов в выражение производной
4. Делаем вывод
Слайд 4Вывод:
если в точке производная меняет знак с положительного на отрицательное значение,
то это точка максимума; если с отрицательного на положительное значение, то это точка минимума.
Слайд 5Задание 12.
Найдите точку минимума функции
у=х3 - 3х2
+ 2
2. Найдите точку максимума функции
у=(х-2)2 (Х- 4) + 5
3. Найдите точку максимума функции
у=(х2 + 289)/ Х
2. Найдите точку максимума функции
у=(х-2)2 (Х- 4) + 5
3. Найдите точку максимума функции
у=(х2 + 289)/ Х
Слайд 8Задачи на наибольшее и наименьшее значение функции на интервале
Алгоритм нахождения наибольшего
(наименьшего)
значения функции:
1. находим производную функции
2. находим нули производной путём приравнивания производной к нулю, решаем полученное уравнение
3. определяем, принадлежат ли полученные точки заданному интервалу, записываем лежащие в пределах интервала.
4. подставляем в исходную функцию (не в производную, а в данную в условии) концы данного интервала и точки (максимума-минимума), лежащие в пределах интервала
5. вычисляем значения функции.
6. выбираем из полученных наибольшее (наименьше) значение, смотря какой вопрос поставлен в задаче, и записываем ответ.
значения функции:
1. находим производную функции
2. находим нули производной путём приравнивания производной к нулю, решаем полученное уравнение
3. определяем, принадлежат ли полученные точки заданному интервалу, записываем лежащие в пределах интервала.
4. подставляем в исходную функцию (не в производную, а в данную в условии) концы данного интервала и точки (максимума-минимума), лежащие в пределах интервала
5. вычисляем значения функции.
6. выбираем из полученных наибольшее (наименьше) значение, смотря какой вопрос поставлен в задаче, и записываем ответ.
Слайд 9Задание 12.
1. Найдите наибольшее значение функции y = x3 + 2x2 -4 x + 4
на отрезке [−2;0].
2. Найдите
наименьшее значение функции y = (х+3) 2 (х+5) - 1
на отрезке [−4;-1].
3. Найдите наименьшее значение функции
на отрезке
на отрезке
на отрезке [−4;-1].
3. Найдите наименьшее значение функции
на отрезке
на отрезке
![Задание 12. 1. Найдите наибольшее значение функции y = x3 + 2x2 -4 x + 4 на отрезке [−2;0].2. Найдите наименьшее значение функции y = (х+3) 2 (х+5)](/img/thumbs/e5521273d272c8e4f234a6bc79d20718-800x.jpg "Презентация по математике при подготовки к ЕГЭ Задание 12. 1. Найдите наибольшее значение функции y = x3 + 2x2 -4 x + 4 на отрезке [−2;0].2.")
Слайд 10Не робей, не бойся ты заданий И откинь сомнения назад, Ты поверь, что
хватит сил и знаний,
Чтоб экзамен «на отлично» сдать.
Успехов !!!
Успехов !!!
