- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад и конспект по математике на тему Векторно-координатный метод решения задач (11 класс)
Содержание
- 1. Презентация и конспект по математике на тему Векторно-координатный метод решения задач (11 класс)
- 2. «Какое чудо – этот переход от слепоты к прозрению, к пониманию сути дела!»М. Вертгеймер.
- 3. Проверка домашнего заданияКак находят координаты вектора, если
- 4. 5. Как вы понимаете выражение «угол между
- 5. 8. Чему равно скалярное произведение перпендикулярных векторов?Скалярное
- 6. 1. Куб с ребром а. Куб
- 7. 2.Правильная треугольная призма сторона основания а,
- 8. 3.Правильная шестиугольная призма сторона основания а,
- 9. 4.Правильная треугольная пирамида МАВС, сторона основания а,
- 10. 5.Правильная четырехугольная пирамида МABCD, сторона основания a,
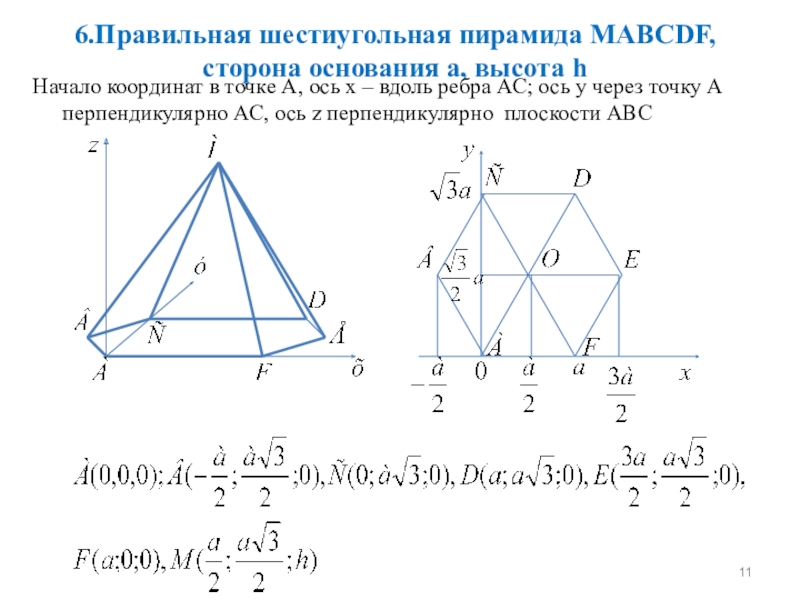
- 11. 6.Правильная шестиугольная пирамида MABCDF, сторона основания a,
- 12. Метод решения хорош, если с самого начала
- 13. Угол между скрещивающимися прямыми — это угол между
- 14. Алгоритм решения задач1.Ввести декартовую систему координат2.Определить координаты
- 15. Угол между прямыми.Для нахождения угла использует формулу
- 16. Вариант 7 С2 в правильной шестиугольной призме
- 17. Угол между прямой и плоскостьюУгол между прямой
- 18. Алгоритм решения1.Ввести декартовую систему координат2.Определить координаты необходимых
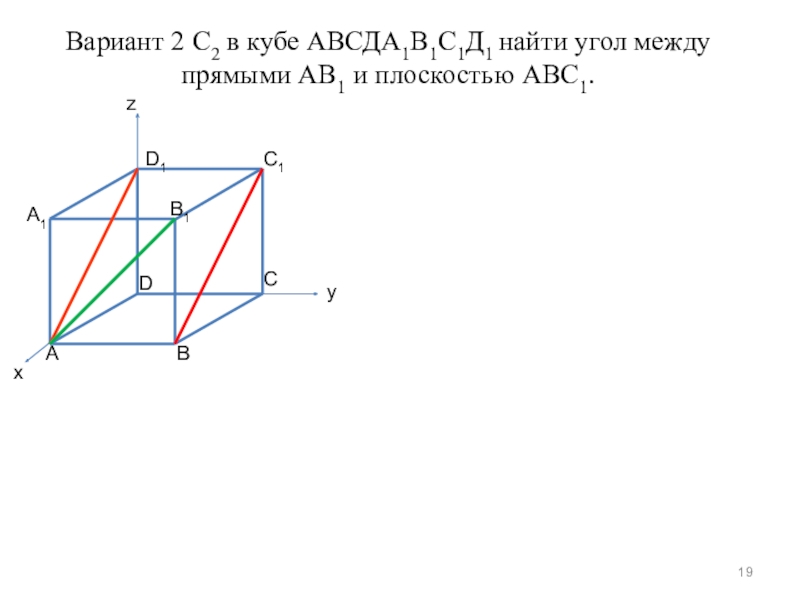
- 19. Вариант 2 С2 в кубе АВСДА1В1С1Д1
- 20. Угол между плоскостямиДля нахождения угла используют формулу
- 21. Алгоритм1.Координаты вектора нормали можно вывести, если известны
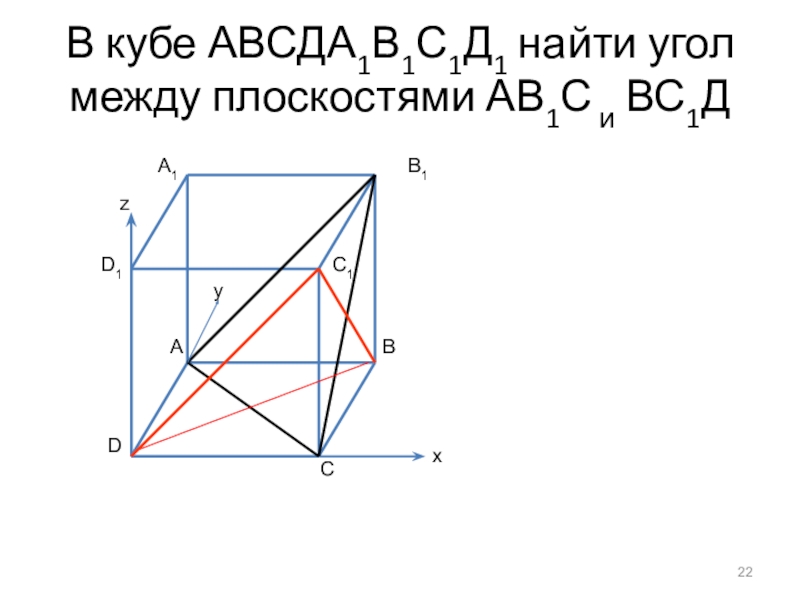
- 22. В кубе АВСДА1В1С1Д1 найти угол между плоскостями АВ1С и ВС1ДС1А1В1DyxCzD1BА
- 23. Помните!Во многих задачах получаются весьма неслабые векторы, координаты
- 24. Замечания по оформлению задачи C2 Подробно
Слайд 1Векторно - координатный метод решения задач С2. МБОУ Бурулятуйская СОШ учитель математики Гармаева
Слайд 3Проверка домашнего задания
Как находят координаты вектора, если известны координаты его начала
-Каждая координата вектора равна разности соответствующих координат его конца и начала.
2. Как находят координаты середины отрезка?
-Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
3. Как находят длину вектора?
4. Как находят расстояние между точками?
-Расстояние между точками вычисляется по формуле
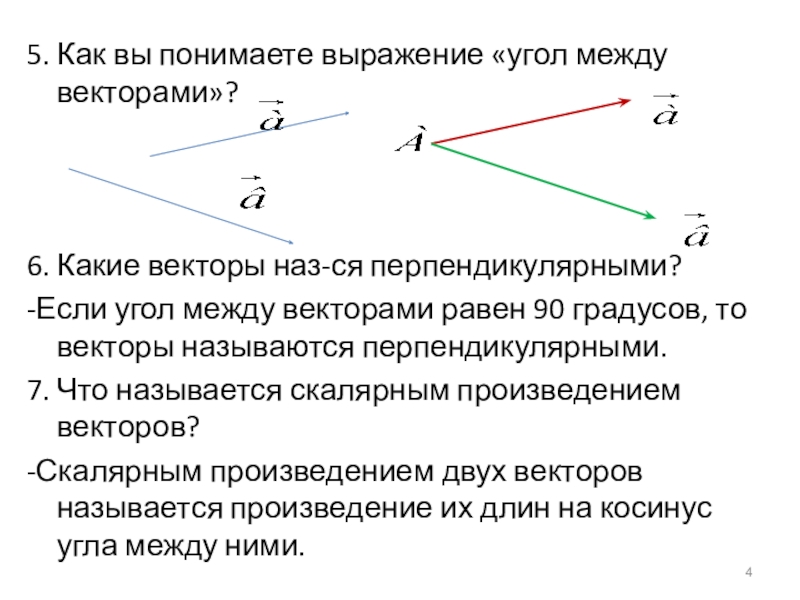
Слайд 45. Как вы понимаете выражение «угол между векторами»?
6. Какие векторы наз-ся
-Если угол между векторами равен 90 градусов, то векторы называются перпендикулярными.
7. Что называется скалярным произведением векторов?
-Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Слайд 58. Чему равно скалярное произведение перпендикулярных векторов?
Скалярное произведение перпендикулярных векторов равно
9. Какой вектор называется направляющим вектором прямой?
- Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой а, либо на прямой, параллельной а.
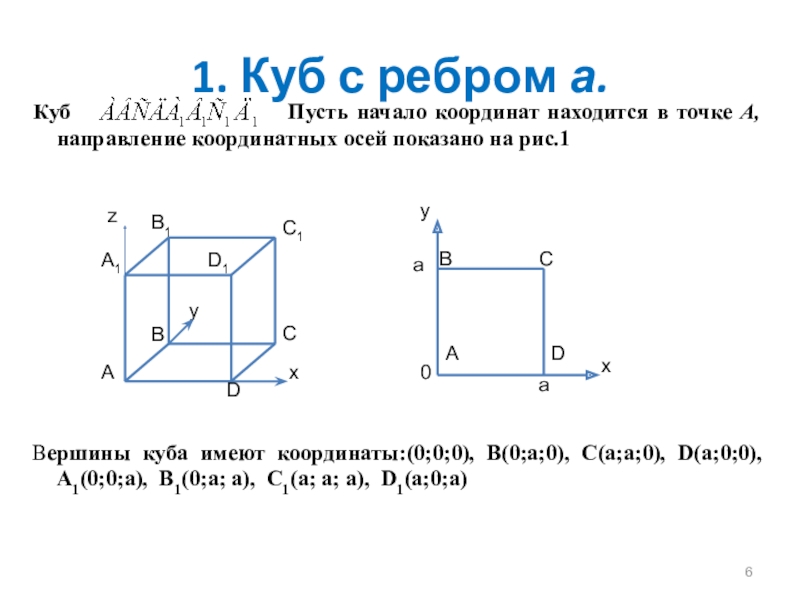
Слайд 61. Куб с ребром а.
Куб
Вершины куба имеют координаты:(0;0;0), В(0;а;0), С(а;а;0), D(а;0;0), A1(0;0;а), B1(0;а; а), С1(а; а; а), D1(а;0;а)
А
A1
B1
C1
C
D1
D
B
y
x
z
0
B
C
x
у
a
D
a
А
Слайд 72.Правильная треугольная призма сторона основания а, боковое ребро b
Начало координат
Тогда вершины призмы имеют координаты:
A(0;0;0), В( ), С(а;0;0), А1(0;0;b), В 1( ), С1( )
y
B
B1
A1
A
C1
C
x
z
A
C
В
0
y
x
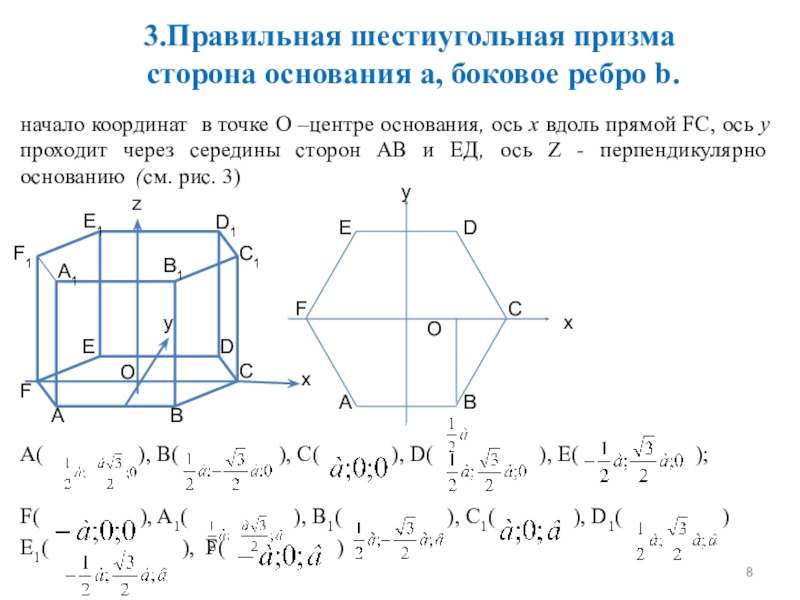
Слайд 83.Правильная шестиугольная призма сторона основания а, боковое ребро b.
начало координат в точке О –центре основания, ось х вдоль прямой FC, ось у проходит через середины сторон АВ и ЕД, ось Z - перпендикулярно основанию (см. рис. 3)
A( ), B( ), C( ), D( ), Е( );
F( ), A1( ), В1( ), С1( ), D1( )
E1( ), F( )
y
С
D1
D
А
F1
В
E1
C1
E
B1
A1
F
x
z
O
A
B
С
x
F
E
D
y
O
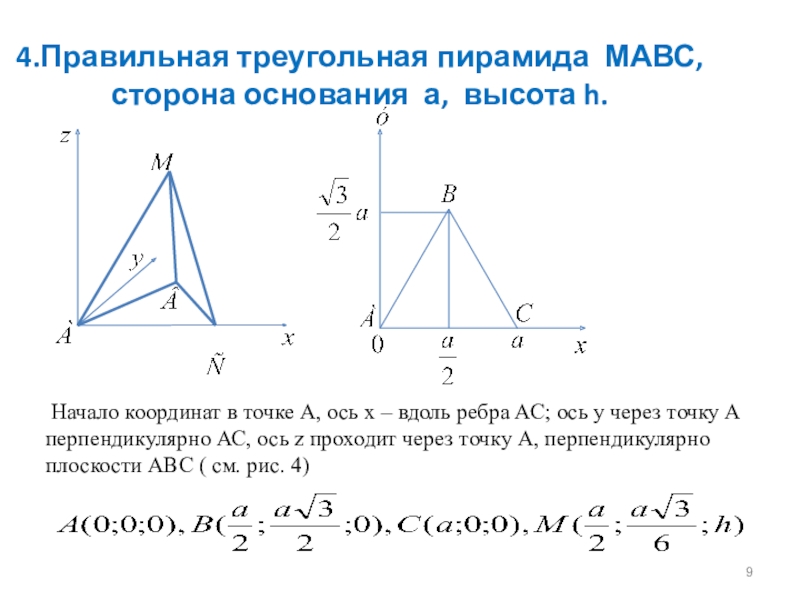
Слайд 94.Правильная треугольная пирамида МАВС, сторона основания а, высота h.
Начало координат
Слайд 105.Правильная четырехугольная пирамида МABCD, сторона основания a, высота h.
Начало координат в
Слайд 116.Правильная шестиугольная пирамида MABCDF, сторона основания a, высота h
Начало координат в
Слайд 12Метод решения хорош, если с самого начала мы можем предвидеть –
Слайд 13Угол между скрещивающимися прямыми — это угол между двумя прямыми, которые пересекаются
Угол между прямой и плоскостью — это угол между самой прямой и ее проекцией на данную плоскость.
Угол между двумя плоскостями — это угол между прямыми, которые лежат в данных плоскостях и перпендикулярны линии пересечения этих плоскостей.
Слайд 14Алгоритм решения задач
1.Ввести декартовую систему координат
2.Определить координаты необходимых точек.
3.Определить координаты направляющих
4. Найти неизвестный угол по формуле.
Слайд 15Угол между прямыми.
Для нахождения угла использует формулу
координатной форме cos
где
направляющие векторы прямых
Слайд 16Вариант 7 С2 в правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все ребра которой
C1
B1
А1
F1
E1
D
D1
y
x
z
F
E
C
B
A
,
Слайд 17Угол между прямой и плоскостью
Угол между прямой и плоскостью вычисляется по
где } – вектор нормали плоскостиα;
- направляющий вектор.
Прямая и плоскость α перпендикулярны тогда и только тогда, когда х1х2 +у1у2 +z1z2=0
Слайд 18Алгоритм решения
1.Ввести декартовую систему координат
2.Определить координаты необходимых точек.
3.Определить координаты направляющих векторов
4. Определим вектор нормали к плоскости
, координаты которого определяются из условия перпендикулярности этого вектора к
векторам плоскости.
4. Найти неизвестный угол по формуле.
Слайд 19 Вариант 2 С2 в кубе АВСДА1В1С1Д1 найти угол между прямыми АВ1
А
D1
A1
C1
B1
С
В
y
z
D
x
Слайд 20Угол между плоскостями
Для нахождения угла используют формулу
-вектор нормали к плоскости
Слайд 21Алгоритм
1.Координаты вектора нормали можно вывести, если известны координаты трех точек плоскости
2. и
3. вектор нормали к плоскости (MNP)
4. Определение координат вектора нормали
5. Вектор нормали к другой плоскости
6. Найдем угол по формуле
Слайд 23Помните!
Во многих задачах получаются весьма неслабые векторы, координаты которых содержат корни и дроби.
Слайд 24
Замечания по оформлению задачи C2
Подробно комментируйте основные моменты решения. Недостаточно просто
Выписывайте координаты точек, с которыми работаете.
Не экономьте на вычислениях. Подставляя числа в формулу для косинуса, напишите эту формулу в исходном виде, затем — с подставленными числами, и только затем проводите вычисления. Это вдвое упростит работу для проверяющего и уменьшит число претензий.
Внимательно читайте условие задачи. Метод координат дает нам только косинус или синус угла — но не ответ. А что, если требуется тангенс? Обидно, если все решение будет правильным, а ответ — совсем не тот, что надо.