«Тоншаловская средняя общеобразовательная школа»
Учитель математики:
Потапова Любовь Николаевна.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Применение подобия
Содержание
- 1. Презентация по математике: Применение подобия
- 2. Тема урока: «Применение подобия к
- 3. Одинаковые по форме, но различные по величине
- 4. Слайд 4
- 5. Вставьте недостающие слова: 1. Многоугольники называются
- 6. 4. Если две стороны одного треугольника ____________
- 7. 7. Прямоугольные треугольники подобны, если _________
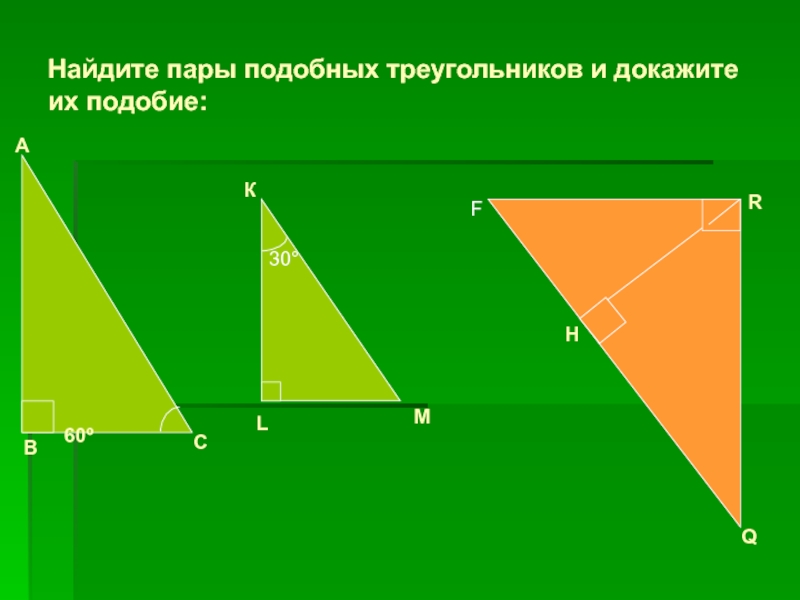
- 8. Найдите пары подобных треугольников и докажите их
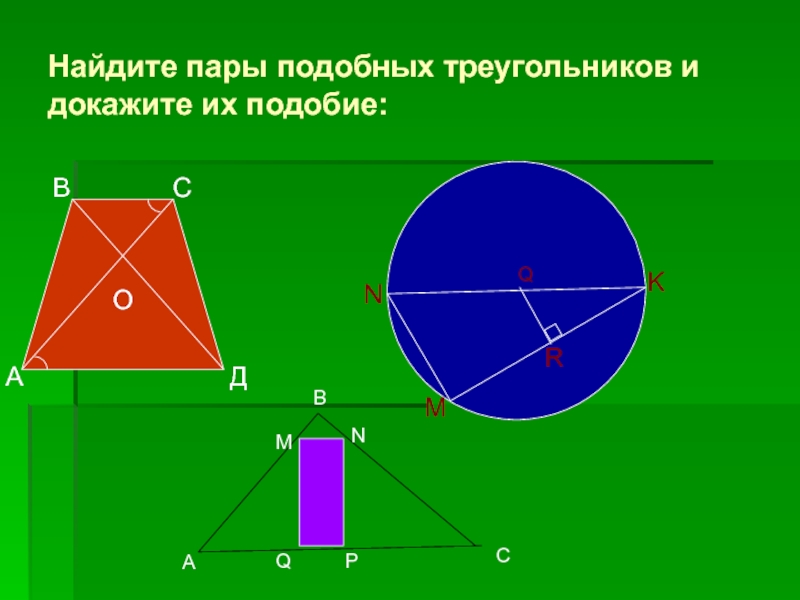
- 9. Найдите пары подобных треугольников и докажите их подобие:ОДСАВNMKRQАМВСРNQ
- 10. Задача 1 План земельного участка имеет форму
- 11. Задача № 2 Длина тени дерева
- 12. Задача № 3 Найдите площадь и периметр
- 13. Задача № 3 Найдите площадь и периметр
- 14. Решение: Данные треугольники подобны. (Докажите их
- 15. Теперь мы знаем, что такое подобие!
Тема урока: «Применение подобия к решению практических задач» Цели урока: Обобщить и систематизировать теоретический материал по теме«Подобие». Рассмотреть применение свойств подобных фигур к решению практических задач.
Слайд 2 Тема урока: «Применение подобия к решению практических задач»
Цели урока:
Обобщить и систематизировать теоретический материал по теме
«Подобие».
Рассмотреть применение свойств подобных фигур к решению практических задач.
Слайд 3Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских
и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса 2 имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров. Своего рода «способ палетки» применяется и сейчас при копировании рисунков, картин и портретов.
Слайд 5Вставьте недостающие слова: 1. Многоугольники называются подобными, если их углы соответственно ______
и стороны одного многоугольника ___________________
сходственным сторонам другого.
2. Число k, равное отношению сходственных сторон подобных многоугольников, называется __________________ подобия.
3. Если два угла одного треугольника ________ двум углам другого треугольника, то такие треугольники подобны.
равны
пропорциональны
коэффициентом
равны
Слайд 64. Если две стороны одного треугольника ____________
двум сторонам другого треугольника
и __________ , заключенные между этими сторонами, ___________ , то такие треугольники подобны.
5. Если _________ стороны одного треугольника пропорциональны ___________ сторонам другого треугольника, то такие треугольники подобны.
6. Прямоугольные треугольники подобны, если гипотенуза и катет одного треугольника ______________ гипотенузе и ________________ другого треугольника.
5. Если _________ стороны одного треугольника пропорциональны ___________ сторонам другого треугольника, то такие треугольники подобны.
6. Прямоугольные треугольники подобны, если гипотенуза и катет одного треугольника ______________ гипотенузе и ________________ другого треугольника.
пропорциональны
углы
равны
три
трем
пропорциональны
катету
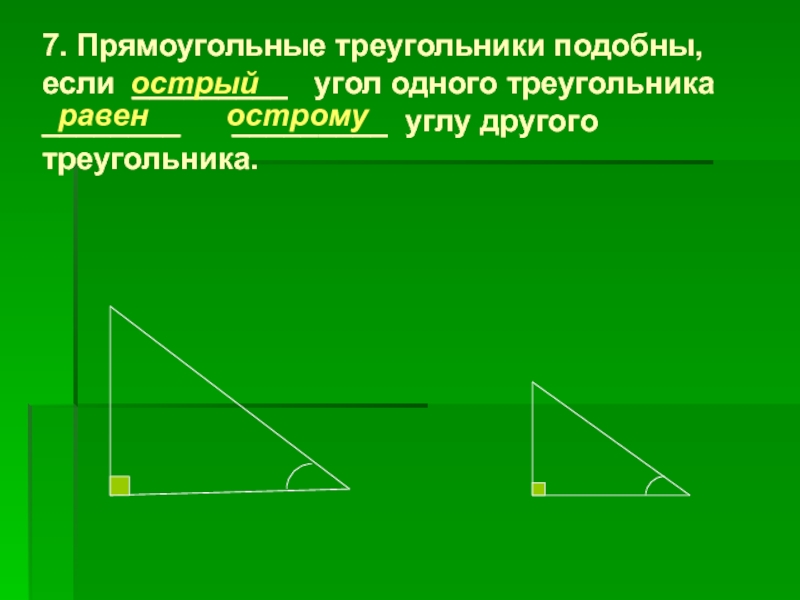
Слайд 77. Прямоугольные треугольники подобны, если _________ угол одного треугольника
________
_________ углу другого треугольника.
острый
равен острому
Слайд 10Задача 1
План земельного участка имеет форму прямоугольного треугольника. Катеты изображенного
на плане треугольника равны 12 см и 10 см. Найти площадь земельного участка, если план выполнен в масштабе 1:100 000.
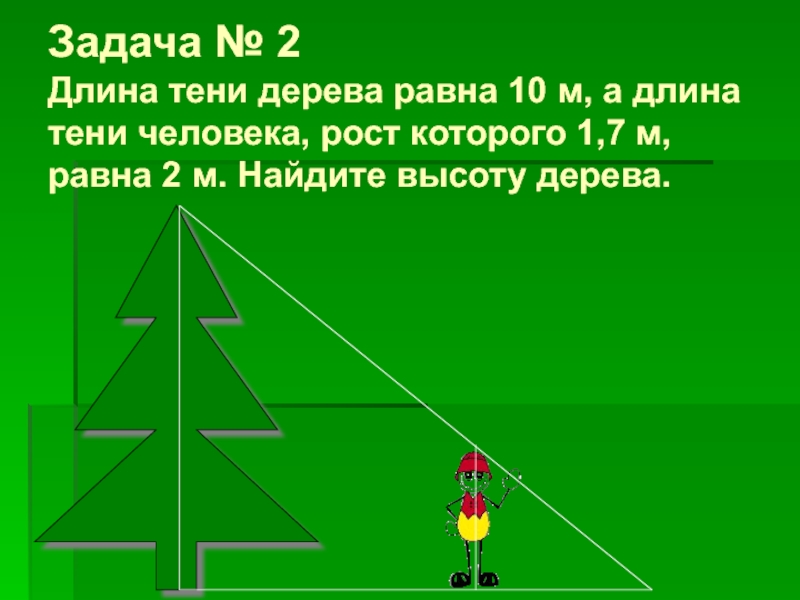
Слайд 11 Задача № 2 Длина тени дерева равна 10 м, а длина тени
человека, рост которого 1,7 м, равна 2 м. Найдите высоту дерева.
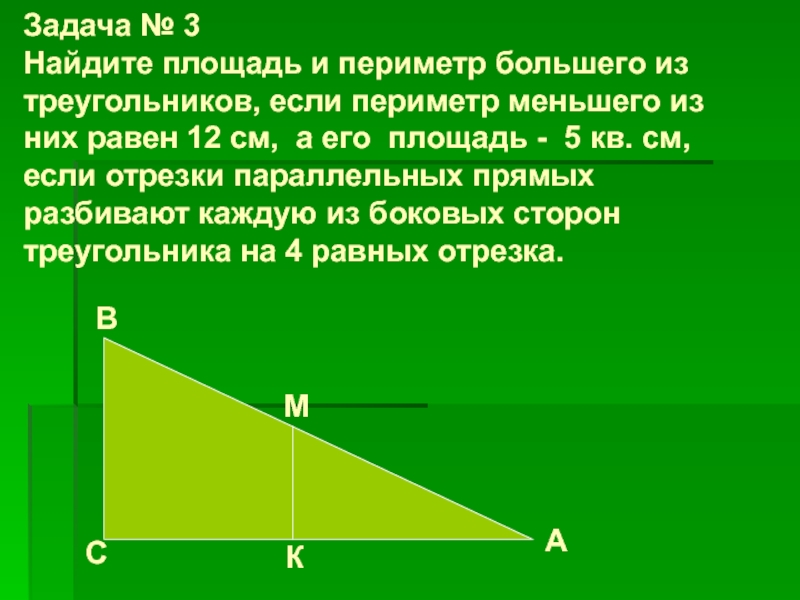
Слайд 12Задача № 3 Найдите площадь и периметр большего из треугольников, если периметр
меньшего из них равен 12 см, а его площадь - 5 кв. см, если отрезки параллельных прямых разбивают каждую из боковых сторон треугольника на 4 равных отрезка.
К
М
С
В
А
Слайд 13Задача № 3 Найдите площадь и периметр большего из треугольников, если периметр
меньшего из них равен 12 см, а его площадь - 5 кв. см, если отрезки параллельных прямых разбивают каждую из боковых сторон треугольника на 4 равных отрезка.
Слайд 14Решение: Данные треугольники подобны. (Докажите их подобие). Коэффициент подобия равен 4.
Отношение периметров подобных треугольников равно коэффициенту подобия,
значит периметр большего треугольника равен:
12 * 4 = 48.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия, значит площадь большего треугольника равна:
5 * 4 * 4 = 80
Ответ: 48см – периметр, 80 кв.см – площадь большего из треугольников.
