- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Последовательность, 10 класс
Содержание
- 1. Презентация по математике Последовательность, 10 класс
- 2. Examples of SequencesThe 3 dots are used to show that a sequence continues
- 3. Recurrence Relations Suppose the formula continues by adding 2 to each term.etc.11
- 4. Recurrence RelationsRecurrence relation:
- 5. Recurrence Relations
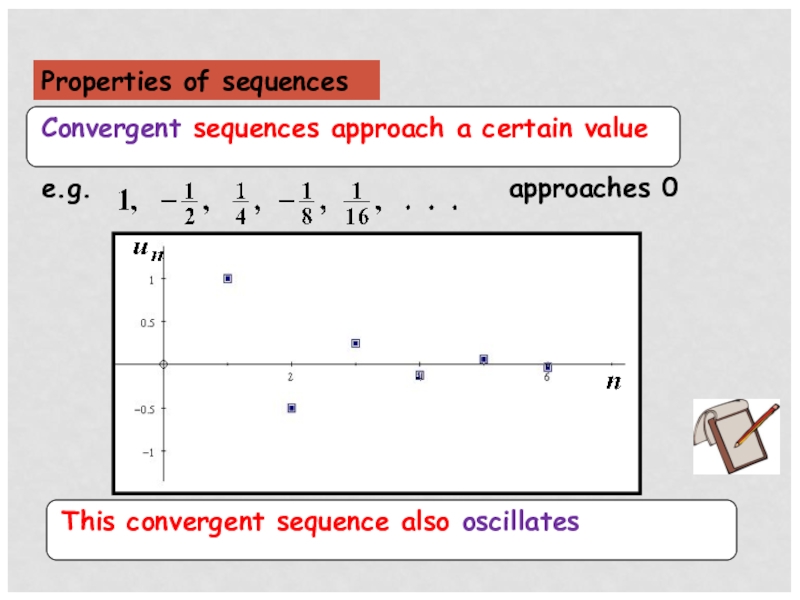
- 6. Properties of sequences
- 7. Properties of sequences
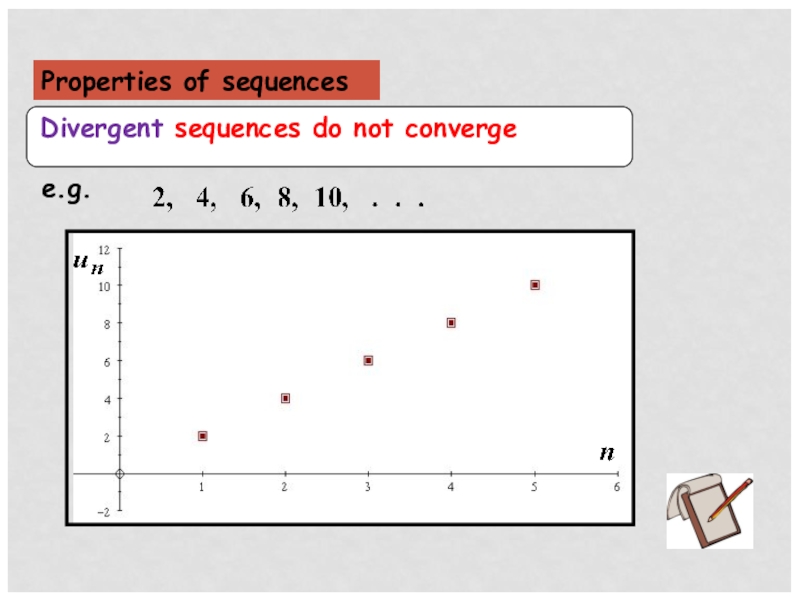
- 8. Properties of sequences
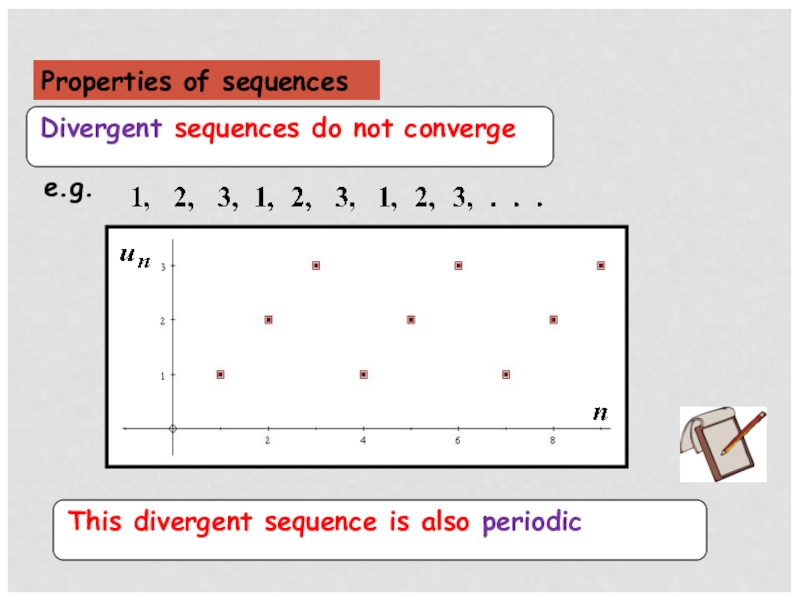
- 9. Properties of sequences
- 10. Properties of sequences
- 11. Introduction of 3 Special sequencesThe triangle number
- 12. Introduction of 3 Special sequencesPascal sequences Based
- 13. Convergent Values It is not always easy
- 14. Exercises1. Write out the first 5 terms
- 15. General Term of a SequenceSome sequences can
- 16. ExercisesWrite out the first 5 terms of
- 17. SeriesWhen the terms of a sequence are
- 18. (b)2. Write the following using sigma notation
Слайд 11Introduction of 3 Special sequences
The triangle number sequence
The
tr=(1/2)r(r+1)
The factorial sequence
fr+1=fr×(r+1), where r=0,1,2,3…… and f0=1
f1=f0×1=1, f2=f1×2=2, f3=f2×3=6
fr=1×2×3×…×r
Factorial r is defined by 0!=1 and (r+1)!=r!×(r+1)
where r=0,1,2,3….. For r≥1, r! is the product of
all the natural numbers from 1 to r.
Read as factorial r or r factorial
Слайд 12Introduction of 3 Special sequences
Pascal sequences Based on multiplication rule as
n=0:1,0,0,0,0…
n=1:1,1,0,0,0…
n=2:1,2,1,0,0…
n=3:1,3,3,1,0…
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Pascal`s triangle which will be studied in chapter 9
Слайд 13Convergent Values
It is not always easy to see what value
To find the value that the sequence converges to we use the fact that eventually ( at infinity! ) the ( n + 1 ) th term equals the n th term.
Слайд 14Exercises
1. Write out the first 5 terms of the following sequences
2. What value does the sequence given by
Слайд 15General Term of a Sequence
Some sequences can also be defined by
The general term can easily be checked by substituting n = 1, n = 2, etc.
Слайд 16Exercises
Write out the first 5 terms of the following sequences
1.
Give the
2.
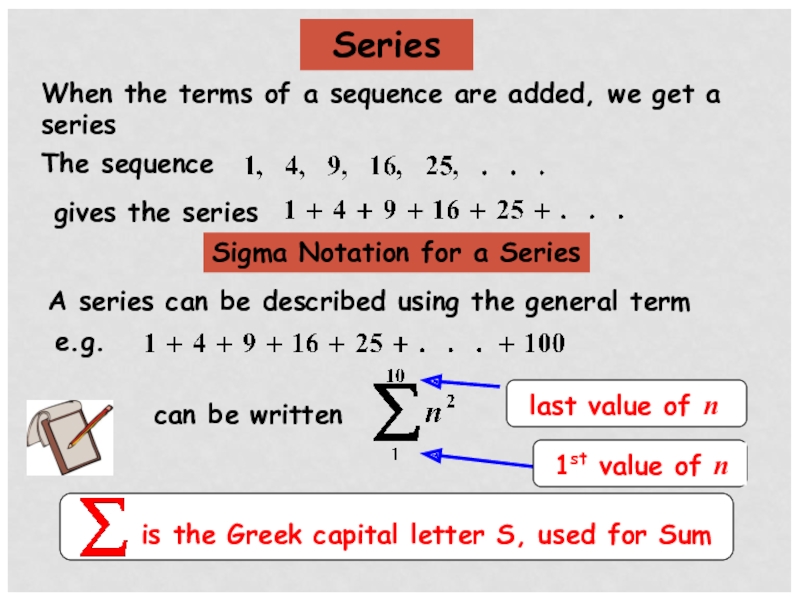
Слайд 17Series
When the terms of a sequence are added, we get a
Sigma Notation for a Series
A series can be described using the general term
Слайд 18(b)
2. Write the following using sigma notation
Exercises
1. Write out the
(a)
(b)
n = 1
n = 2
n = 20