- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике показательная функция
Содержание
- 1. Презентация по математике показательная функция
- 2. СодержаниеУчебный материалСамоконтрольОб автореВыход
- 3. ОпределениеПусть а > 1 и
- 4. Свойства функции1.
- 5. Свойства функции1.
- 6. ОпределениеПоказательной функцией называетсяфункция вида
- 7. График показательной функции1
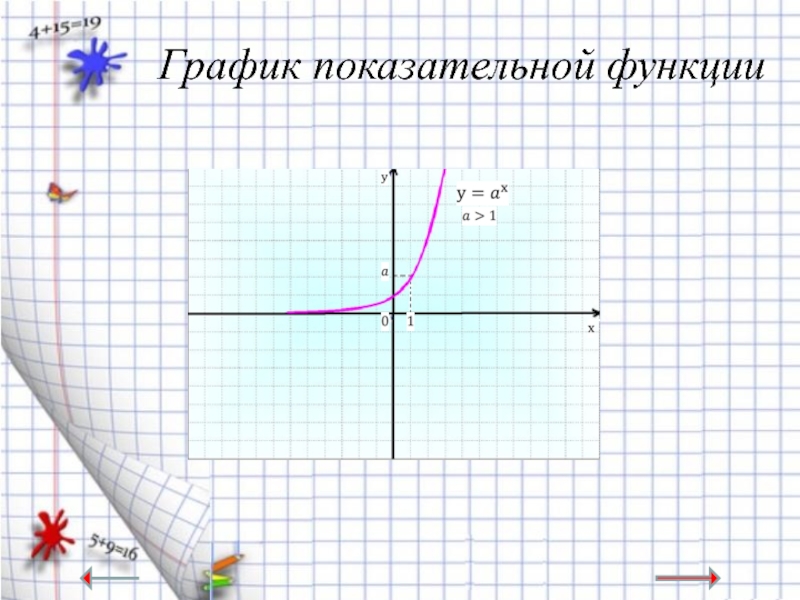
- 8. График показательной функции
- 9. Свойства показательной функции При а>1: 1.
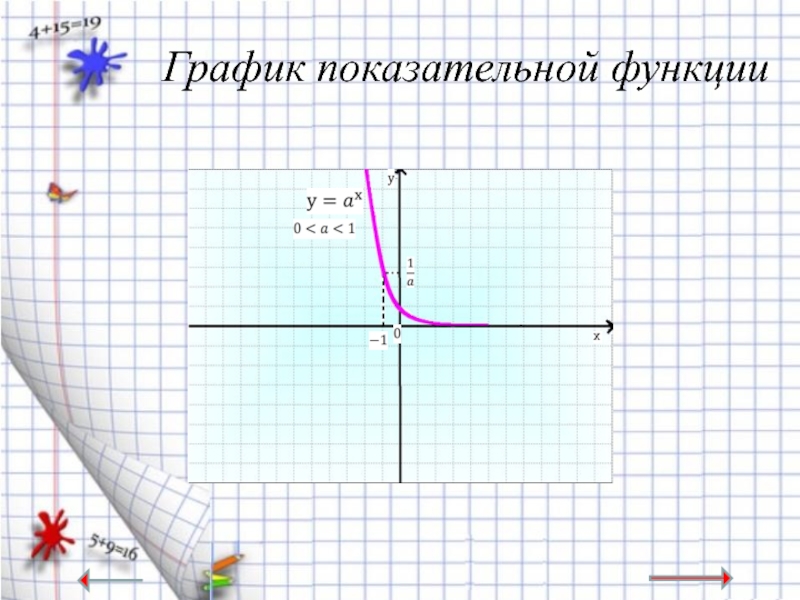
- 10. Свойство показательной функции При 0
- 11. Перечислить свойство функции и постройте ее график
- 12. Перечислить свойство функции и постройте ее график
- 13. Теорема 1Если
- 14. Теорема 2Если
- 15. Пример 1Решим уравнение:
- 16. Пример 2Решим неравенство: График функции
- 17. Теорема 3Если 0 < а < 1, то равенствосправедливо тогда и только тогда, когда t=s.
- 18. Теорема 4Если 0 < а
- 19. Пример 3Решим уравнение: Построим в системе
- 20. Пример 4Решим неравенство: Экспонента
- 21. Самоконтроль. Пример 1Какая из функций является показательной
- 22. Самоконтроль. Пример 2Найти множество значений функции
- 23. Самоконтроль. Пример 3Укажите возрастающую функцию
- 24. Самоконтроль. Пример 4Какое из следующих чисел входит
- 25. Самоконтроль. Пример 5Найти область определения функции
- 26. Самоконтроль. Пример 6Укажите, какие из заданных функцийограничены снизу
- 27. Неверно…
- 28. Молодец!
- 29. Об авторе(С) Мухина Эльвина Вадиславовна, Russia.2011Xoчу выразить
СодержаниеУчебный материалСамоконтрольОб автореВыход
Слайд 4Свойства функции
1.
;
2. не является ни четной, ни нечетной;
3. возрастает;
4. не ограничена сверху, ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. ;
8. выпукла вниз.
2. не является ни четной, ни нечетной;
3. возрастает;
4. не ограничена сверху, ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. ;
8. выпукла вниз.
Слайд 5Свойства функции
1.
;
2. не является ни четной, ни нечетной;
3. возрастает;
4. не ограничена сверху, ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. ;
8. выпукла вниз.
2. не является ни четной, ни нечетной;
3. возрастает;
4. не ограничена сверху, ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. ;
8. выпукла вниз.
Слайд 6Определение
Показательной функцией называется
функция вида
где
а заданное число, х - переменная.
Запиши в тетрадь
Слайд 9Свойства показательной функции
При а>1:
1. область определения - множество
R;
2. область значений - множество положительных R;
3. функция возрастает;
4. функция непрерывна.
2. область значений - множество положительных R;
3. функция возрастает;
4. функция непрерывна.
Слайд 10 Свойство показательной функции
При 0
область определения - множество R;
2. область значений - множество положительных R;
3. функция убывает;
4. функция непрерывна.
2. область значений - множество положительных R;
3. функция убывает;
4. функция непрерывна.
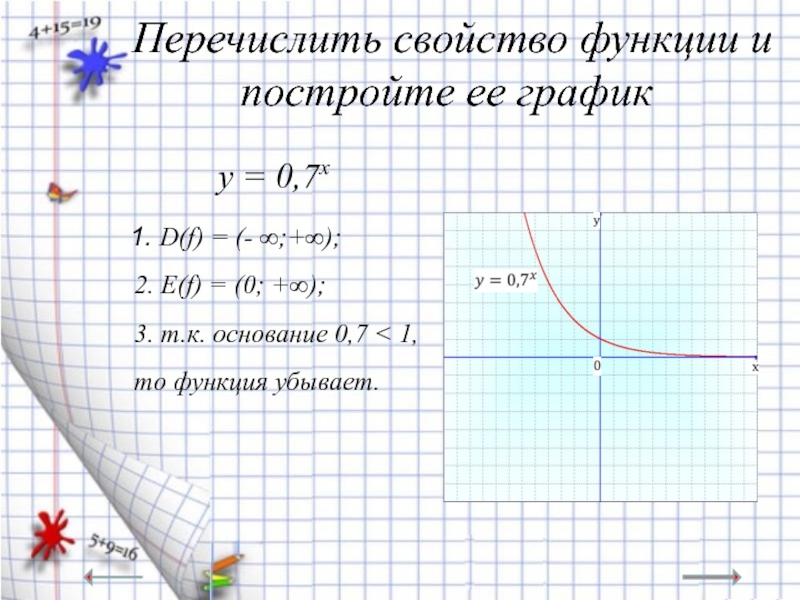
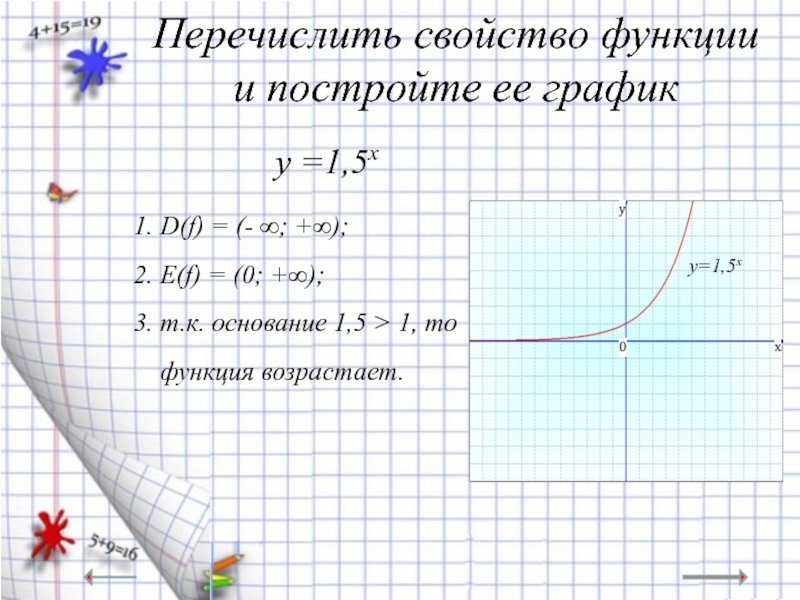
Слайд 11Перечислить свойство функции и постройте ее график
1. D(f) = (- ∞;+∞);
2. E(f) = (0; +∞);
3. т.к. основание 0,7 < 1,
то функция убывает.
у = 0,7х
Слайд 12Перечислить свойство функции и постройте ее график
у =1,5х
1. D(f) = (- ∞; +∞);
2. E(f) = (0; +∞);
3. т.к. основание 1,5 > 1, то
функция возрастает.
у=1,5х
Слайд 14Теорема 2
Если , то неравенство
справедливо тогда и только тогда, когда
; неравенство справедливо
тогда и только тогда, когда .
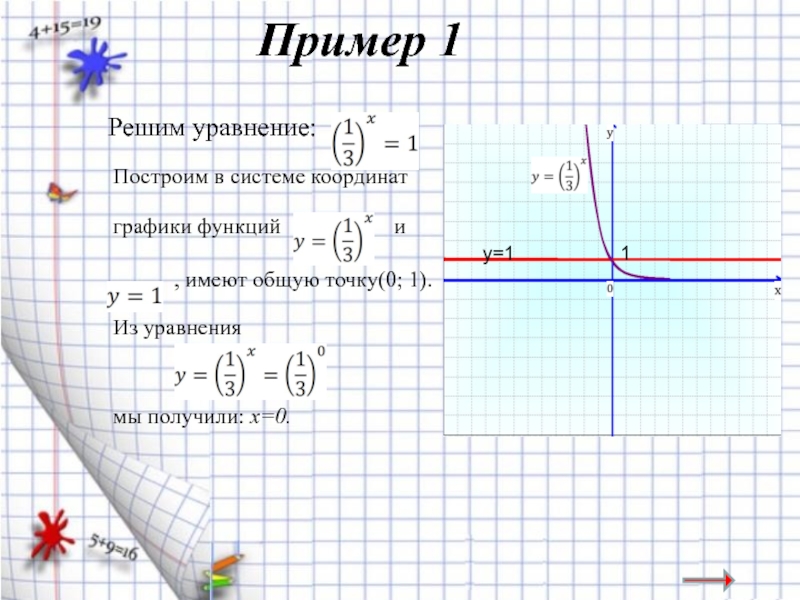
Слайд 15Пример 1
Решим уравнение:
Построим в системе координат
графики функций и
, имеют общую точку(0; 1).
Из уравнения
мы получили: х=0.
графики функций и
, имеют общую точку(0; 1).
Из уравнения
мы получили: х=0.
1
y=1
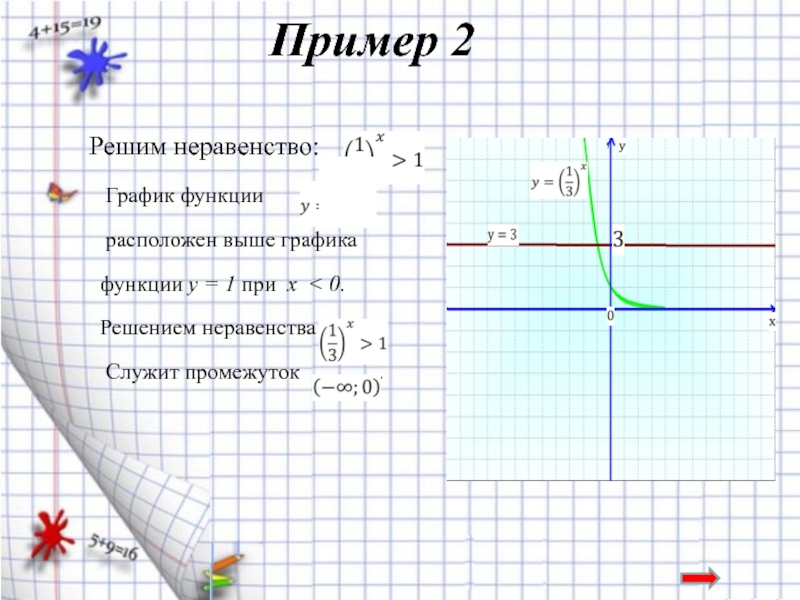
Слайд 16 Пример 2
Решим неравенство:
График функции
расположен выше графика
функции у = 1 при х < 0.
Решением неравенства
Служит промежуток .
Решением неравенства
Служит промежуток .
Слайд 18 Теорема 4
Если 0 < а < 1, то неравенство
справедливо тогда и только тогда, когда
х < 0; неравенство справедливо
тогда и только тогда, когда х >0.
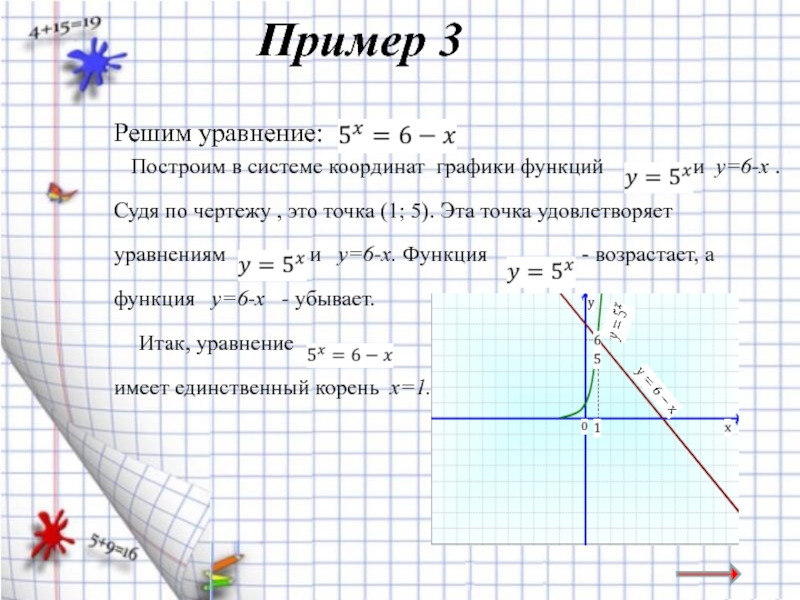
Слайд 19Пример 3
Решим уравнение:
Построим в системе координат графики функций
и у=6-х .
Судя по чертежу , это точка (1; 5). Эта точка удовлетворяет
уравнениям и у=6-х. Функция - возрастает, а
функция у=6-х - убывает.
Итак, уравнение
имеет единственный корень х=1.
Судя по чертежу , это точка (1; 5). Эта точка удовлетворяет
уравнениям и у=6-х. Функция - возрастает, а
функция у=6-х - убывает.
Итак, уравнение
имеет единственный корень х=1.
Слайд 20Пример 4
Решим неравенство:
Экспонента
лежит выше прямой у=6-х, если х > 1- это
видно на рисунке (пример 3). Значит, решением неравенства
можно записать так: .
видно на рисунке (пример 3). Значит, решением неравенства
можно записать так: .
Слайд 29Об авторе
(С) Мухина Эльвина Вадиславовна, Russia.2011
Xoчу выразить слова благодарности своим родителям
за мое воспитание. Также хочу поблагодарить своего научного руководителя Цвырко Олега Леонидовича….
меню
