- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Подготовка к ЕГЭ. Задачи с параметром
Содержание
- 1. Презентация по математике Подготовка к ЕГЭ. Задачи с параметром
- 2. СодержаниеКвадратные уравнения с параметромБиквадратные уравнения с параметромПоказательные и логарифмические уравнения с параметромТригонометрические уравнения с параметром
- 3. Квадратные уравнения с параметромНайти значения параметра p
- 4. Биквадратные уравнения с параметромНайдите все значения а,
- 5. Показательные и логарифмические уравнения с параметром Найдите
- 6. Тригонометрические уравнения с параметром Найти все значения
- 7. Найдите все значения а, при которых область
- 8. При a=1 неравенство
- 9. .Получили: решением неравенства
- 10. При каких значениях а сумма
- 11. На промежутке (0;1] функция
- 12. Найти значения параметра p при которых система имеет единственное решение. Решение:Метод исключения:Ответ: p=4Назад
- 13. Найти сумму всех значений параметра p при
- 14. Найти значения параметра P при которых уравнение имеет один корень.Решение: Ответ: 0; 1; 2; 3; 6. Назад
- 15. Решение:Рассмотрим функциюУпростим: Значения указанных в задаче выражений
- 16. Ответ: хНазад
- 17. Найдите все значения а, для которых при
- 18. ПустьПри графики функций
- 19. Перепишем в видеПусть Рассмотрим функцию Производная На
- 20. Рассмотрим уравнение
- 21. Найти все значения параметра а при каждом
- 22. Если , тот.е. Если x=-1, то y=13,
- 23. Найти все значения параметра а, при каждом
- 24. Слайд 24
- 25. Слайд 25
Слайд 2Содержание
Квадратные уравнения с параметром
Биквадратные уравнения с параметром
Показательные и логарифмические уравнения с
Тригонометрические уравнения с параметром
Слайд 3Квадратные уравнения с параметром
Найти значения параметра p при которых система имеет
Найти сумму всех значений параметра p при которых уравнение имеет одно решение
Найти значения параметра P при которых уравнение имеет один корень.
К содержанию
Решение
Решение
Решение
Слайд 4Биквадратные уравнения с параметром
Найдите все значения а, для которых при каждом
Найдите все значения а, для которых при каждом х из промежутка
(-3;1] значение выражения не равно значению выражения
Решение
Решение
К содержанию
Слайд 5Показательные и логарифмические уравнения с параметром
Найдите все значения а, при которых
содержит ровно три целых числа.
При каких значениях а сумма
больше 1 при всех х ?
К содержанию
Решение
Решение
Слайд 6Тригонометрические уравнения с параметром
Найти все значения параметра p, при которых
не имеет корней.
Найдите все значения параметра p , при которых выражение
будет равно 2 хотя бы при одном значении x.
Найти все значения параметра а, при каждом из которых оба числа
и являются решениями неравенства
Найти все значения параметра а, при каждом из которых функция
возрастает на всей числовой прямой и не имеет критических точек.
К содержанию
Решение
Решение
Решение
Решение
Слайд 7Найдите все значения а, при которых область определения функции содержит ровно 3
Решение.
Область определения функции
Преобразуем левую часть неравенства (*) :
Неравенство (*) равносильно системе:
Решим неравенство методом интервалов.
Слайд 8
При a=1 неравенство
Если а≠1, тогда в (**) где x>0, x ≠1
Рассмотрим целые решения неравенства при различных значениях параметра a>0, а≠1
0
Это решение не удовлетворяет требованиям задачи
1
Это решение не удовлетворяет требованиям задачи
a=3
Это решение не удовлетворяет требованиям задачи
a>3
Слайд 9
.
Получили: решением неравенства
Этот отрезок содержит 3 целых числа в том случае, если
Ответ: Область определения данной функции содержит 3 целых числа при
Назад
Слайд 11На промежутке (0;1] функция
Таким образом, при a>24 при всех t из промежутка
решений нет.
a>1 - возрастающая
На промежутке (0;1] функция является непрерывной и возрастающей.
При при всех t из промежутка
Ответ:
Назад
Слайд 12Найти значения параметра p при которых система имеет единственное решение.
Решение:
Метод исключения:
Ответ:
Назад
Слайд 13Найти сумму всех значений параметра p при которых уравнение имеет одно
Решение:
Коэффициент перед равен 0
Дискриминант равен 0
Ответ:
Назад
Слайд 14Найти значения параметра P при которых уравнение имеет один корень.
Решение:
Ответ: 0;
Назад
Слайд 15Решение:
Рассмотрим функцию
Упростим:
Значения указанных в задаче выражений не равны друг другу
Так как f(0)=-3, то уравнение f(t)=0 имеет 2 корня, один из которых положительный, другой отрицательный.
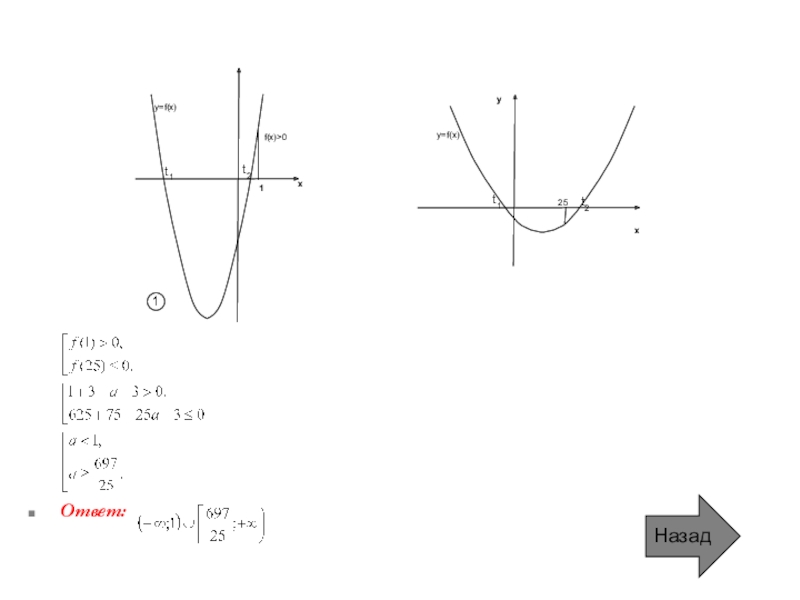
Условие f(t) ≠0 на промежутке [1;25) выполняется, если график квадратичной функции f(t) имеет вид:
Найдите все значения а, для которых при каждом х из промежутка (-5;1] значение выражения не равно значению выражения .
Слайд 17Найдите все значения а, для которых при каждом х из промежутка (-3;1]
Решение.
Используем графическое представление.
чётная функция;
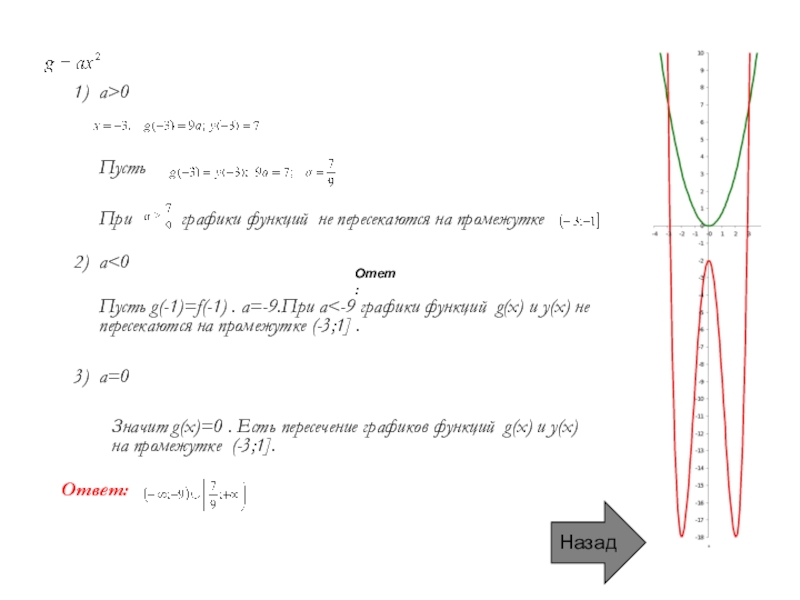
Слайд 18Пусть
При графики функций не пересекаются на промежутке
Пусть g(-1)=f(-1) . a=-9.При a<-9 графики функций g(x) и y(x) не пересекаются на промежутке (-3;1] .
Значит g(x)=0 . Есть пересечение графиков функций g(x) и y(x) на промежутке (-3;1].
1) a>0
2) a<0
3) a=0
Ответ:
Отет:
Назад
Слайд 19Перепишем в виде
Пусть
Рассмотрим функцию
Производная
На отрезке [-1;1] есть единственная
Так как функция непрерывна на отрезке [-1;1] и множество её значений [-7;11], то уравнение не имеет корней, если p не лежит во множестве [-7;11],т.е.
Ответ:
Назад
Найти все значения параметра p при которых уравнение не имеет корней
Слайд 20Рассмотрим уравнение
Преобразуем
Делим на
Пусть tgx=a
Уравнение имеет корни, если его D≥0
Ответ:
Назад
Найти все значения параметра p, при которых выражение
будет равно 2 хотя бы при одном значении x
Слайд 21Найти все значения параметра а при каждом из которых оба числа
Решение.
Решением неравенства является множество [-2;0)∪[13;18)
Найдём все значения параметра а, при каждом из которых оба числа 4sina-3 и 8cos2a+16sina+1 принадлежат множеству [-2;0)∪[13;18)
Пусть
подставим во второе число
По условию x и являются решениями неравенства, т.е. принадлежат множеству
[-2;0)∪[13;18)
т.к.-7≤4sina-3 ≤1 , то x∉[13;18)
-парабола с вершиной (-1;13)
Слайд 22Если , то
т.е.
Если x=-1, то y=13, т.е. x и y
т.е. x=-1, т.е.
Ответ:
Назад
Слайд 23Найти все значения параметра а, при каждом из которых функция
Решение.
Функция возрастает на всей числовой прямой и не имеет критических, если при всех значениях х.
Пусть t = sinx , рассмотрим f(t)
Решая систему получаем
Ответ:
Назад










![Презентация по математике Подготовка к ЕГЭ. Задачи с параметром На промежутке (0;1] функция является непрерывной На промежутке (0;1] функция является непрерывной](/img/thumbs/5860cc6ed1a6d99a6fc60f25f0c4fb91-800x.jpg)




![Презентация по математике Подготовка к ЕГЭ. Задачи с параметром Найдите все значения а, для которых при каждом х из промежутка Найдите все значения а, для которых при каждом х из промежутка (-3;1] значение выражения](/img/thumbs/01f79d56a7dd5859f2b248d48477df5e-800x.jpg)
![Презентация по математике Подготовка к ЕГЭ. Задачи с параметром Перепишем в видеПусть Рассмотрим функцию Производная На отрезке [-1;1] есть единственная Перепишем в видеПусть Рассмотрим функцию Производная На отрезке [-1;1] есть единственная критическая точка t=0Так как функция непрерывна](/img/thumbs/f81e25e84497e498217e4ad9bca3d7d3-800x.jpg)











