- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Простейшие тригонометрические уравнения
Содержание
- 1. Презентация по математике по теме Простейшие тригонометрические уравнения
- 2. Простейшие тригонометрические уравнения Определение арксинуса. Уравнение sin
- 3. Слайд 3
- 4. Определение арккосинусаАрккосинусом числа а называется такой угол
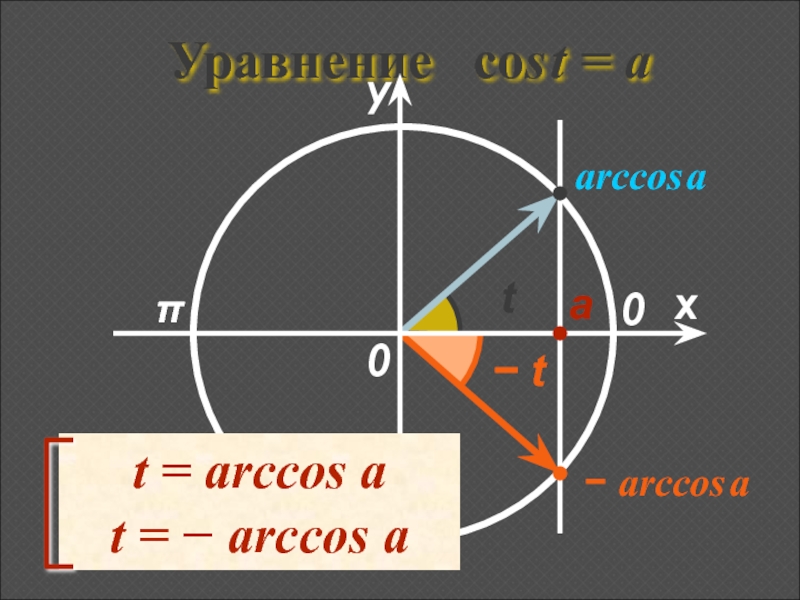
- 5. Уравнение cos t = а πxу0аarccos a− arccos a0t− t
- 6. Уравнение cost = a0xy2. Отметить точку а
- 7. Примеры уравнений0xy-11№ 136, 137
- 8. Частные случаи уравнения cost = axycost = 0cost = -1cost = 1
- 9. Определение арксинусаАрксинусом числа а называется такой угол
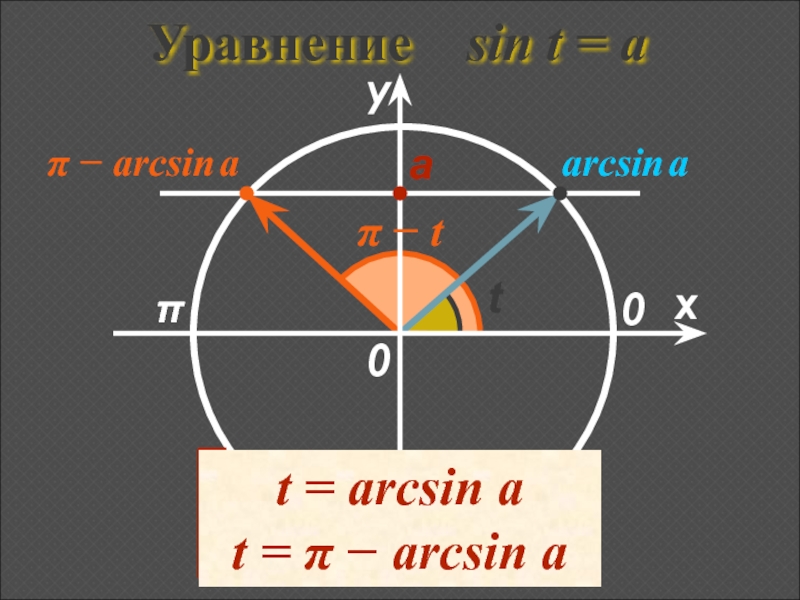
- 10. Уравнение sin t = а πxу0аarcsin aπ − arcsin a0tπ − t
- 11. Уравнение sint = a0xy2. Отметить точку а
- 12. Примеры уравнений0xy-11№ 138, 139
- 13. Частные случаи уравнения sint = axysint = 0sint = -1sint = 1
- 14. Определение арктангенсаАрктангенсом числа а называется такой угол
- 15. arctg aУравнение tg t = а 1xу0tt = arctg aЛиния тангенсова−1−11№ 140, 141
- 16. Домашнее заданиеП. 9 (Колмогоров А. Н. )№ 136 – 141 (в, г)
- 17. Спасибо за внимание!
Слайд 2Простейшие тригонометрические уравнения
Определение арксинуса.
Уравнение sin t = asin
Определение арккосинуса.
Уравнение cos t = acos t = a.
Определение арктангенса.
Уравнение tg t = a.
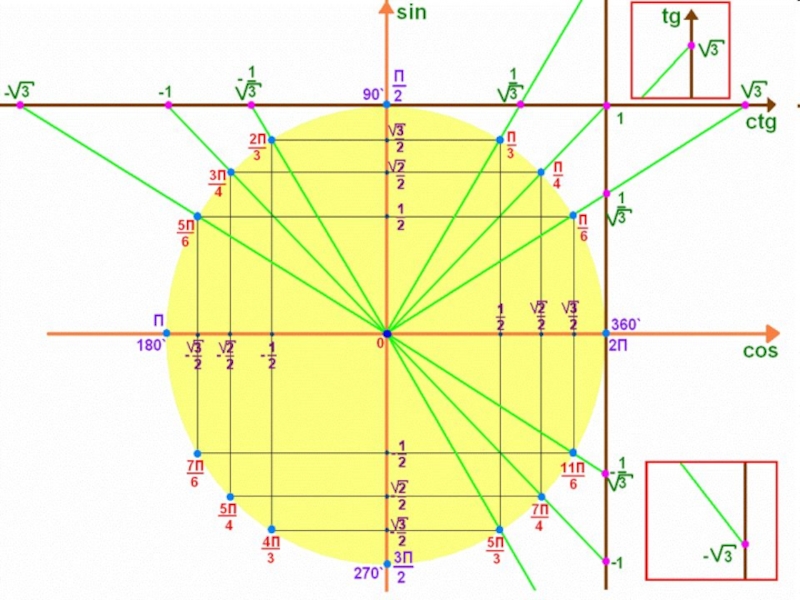
Слайд 4Определение арккосинуса
Арккосинусом числа а называется
такой угол из промежутка [ 0;
косинус которого равен а, где |а| ≤ 1.
arccos a = t , cos t = a
где t ∈ [ 0; π]
а ∈ [− 1; 1]
cos(arccos a) = a, a ∈ [-1; 1]
arccos(cos t) = t, t ∈ [ 0; π]
№ 122 стр 68
Слайд 6Уравнение cost = a
0
x
y
2. Отметить точку а на оси абсцисс.
3. Построить
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения cost = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
-t1
-1
1
Слайд 9Определение арксинуса
Арксинусом числа а называется
такой угол из промежутка [− 0,5π;
синус которого равен а, где |а| ≤ 1.
arcsin a = t , sin t = a
где t ∈ [− 0,5π; 0,5π]
а ∈ [− 1; 1]
sin(arcsin a) = a, а ∈ [− 1; 1]
arcsin(sin t) = t, t ∈ [− 0,5π; 0,5π]
№ 121 стр 67
Слайд 11Уравнение sint = a
0
x
y
2. Отметить точку а на оси ординат.
3. Построить
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения sint = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
-t1
-1
1
Слайд 14Определение арктангенса
Арктангенсом числа а называется
такой угол из промежутка (− 0,5π;
тангенс которого равен а.
arctg a = t , tg t = a
где t ∈ (− 0,5π; 0,5π)
tg(arctg a) = a
arctg(tg t) = t, t ∈ (− 0,5π; 0,5π)
arctg (−a) = − arctg a
№ 123 стр 68


![Презентация по математике по теме Простейшие тригонометрические уравнения Определение арккосинусаАрккосинусом числа а называется такой угол из промежутка [ 0; Определение арккосинусаАрккосинусом числа а называется такой угол из промежутка [ 0; π], косинус которого равен а, где](/img/thumbs/29cfe9f07a5507a79a8b3a91c26131a7-800x.jpg)



![Презентация по математике по теме Простейшие тригонометрические уравнения Определение арксинусаАрксинусом числа а называется такой угол из промежутка [− 0,5π; Определение арксинусаАрксинусом числа а называется такой угол из промежутка [− 0,5π; 0,5π], синус которого равен а, где](/img/thumbs/2050913ec080ec8c5cc84d4c91903f38-800x.jpg)