Презентация, доклад по математике по теме Метод интервалов (9 класс)

Содержание

1. Презентация по математике по теме Метод интервалов (9 класс)
2. Если функция задана формулой вида: f
3. 5- 4 + + -Ответ:Решение.Решить
4. Работа в группах1) (х-1)(х+4) ≤ 0.2) (х+2)(х-5)
5. ФизкультминуткаРасслабимся не отходя от математики:1. Покажите направление ветвей параболы, если старший коэффициент параболы а>0 ,а
6. 7- 2 + - -Ответ:Решение.Решить
7. Решите методом интервалов неравенства:2) x(x +
8. Найдите область определения функции1)2) Решите систему неравенств1)2)
9. Спасибо за урок

Если функция задана формулой вида: f (x)=(x-x1)(x-x2)…(x- xn), где х- переменная, а х 1,х2 ,…,хn, не равные друг другу числа. Эти числа являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями

Главная
Алгебра
Презентация по математике по теме Метод интервалов (9 класс)

Слайд 1Решение неравенств методом интервалов
Автор: Учитель математики
МБОУ СКОШ №36

г. Озёрск

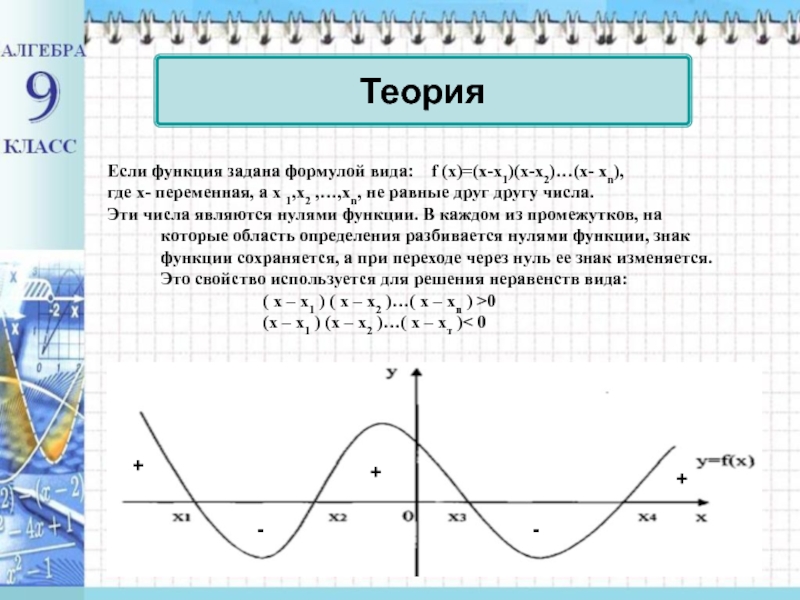
Слайд 2Если функция задана формулой вида: f (x)=(x-x1)(x-x2)…(x- xn),
где х-

переменная, а х 1,х2 ,…,хn, не равные друг другу числа.
Эти числа являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется. Это свойство используется для решения неравенств вида:
( х – х1 ) ( х – х2 )…( х – хn ) >0
(x – x1 ) (x – x2 )…( x – xт )< 0

Теория

Если функция задана формулой вида: f (x)=(x-x1)(x-x2)…(x- xn), где х- переменная, а х 1,х2 ,…,хn, не

Слайд 3

5

- 4
+
+
-
Ответ:
Решение.
Решить неравенство (x –

5)(x + 4)(x + 5) ≤ 0

1. Рассмотрим функцию f(x) = (x – 5)(x + 4)(x + 5)

Нули функции: f(x) = 0
(x – 5)(x + 4)(x + 5)=0
x = 5, x= - 4, x = - 5

- 5

(- ∞;-5] U [-4; 5]

2. Область определения функции D(f) = R

5. х

(- ∞;-5] U [-4; 5]

5- 4 + + -Ответ:Решение.Решить неравенство (x – 5)(x + 4)(x + 5) ≤ 01.

Слайд 4Работа в группах
1) (х-1)(х+4) ≤ 0.

2) (х+2)(х-5) ≤ 0.

3) (х-6)(х-4) >

· [-4;1],(-3;1),[0;1],(-4;1),[-4;-2]

[-2;-5],(2;5),[0;2],[-1;2),[3;-5]

(7;10),[-5;3],[8;11),[-6;4),[-7;0)

Определить промежуток , который принадлежит неравенству

Слайд 5Физкультминутка
Расслабимся не отходя от математики:
1. Покажите направление ветвей параболы, если старший

коэффициент параболы а>0 ,а<0
2. Покажите главное направление оси абсцисс правой рукой, а оси ординат левой рукой. Теперь покажите это быстро.
3. посмотрите, не поворачивая головы, на тетрадь и на затылок соседа.
                      Из-за маленькой ошибки
                      Вижу ваши я улыбки
                      Ничего! Получится!
                      Ведь не делает ошибки,
                      Кто совсем не учится.