- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Логарифмическая функция
Содержание
- 1. Презентация по математике по теме Логарифмическая функция
- 2. Содержание: Логарифм2.Логарифмическая функция3.Логарифмические уравнения4.Логарифмические неравенства
- 3. Определение логарифмаСвойства логарифмовЛОГАРИФМЫИсториялогарифмаЛогарифмическая линейкаПрименение логарифмов
- 4. История логарифма Логарифмы были изобретены Джоном Непером
- 5. Логарифмы с основанием e ввел учитель математики
- 6. Коши первый предложил ввести различные знаки для
- 7. После появления первых таблиц появились таблицы, содержащие
- 8. В течение более чем трех столетий все
- 9. Период полураспада вещества. λ = ln2/T T1/2 = λ-1ln2. λ-постоянная распадаПрименение логарифмов в физике.
- 10. Коэффициент звукоизоляции. Δ L = 10lg(I2/I1), дБI1
- 11. Логарифм в природеВ устройстве уха можно заметить
- 12. Первым ученым, открывшим эту кривую, был Р.Декарт.Затем
- 13. В 1846 г. физиолог Вебер установил зависимость
- 14. Логарифмы в музыке.Величина какого-либо интервала в долях
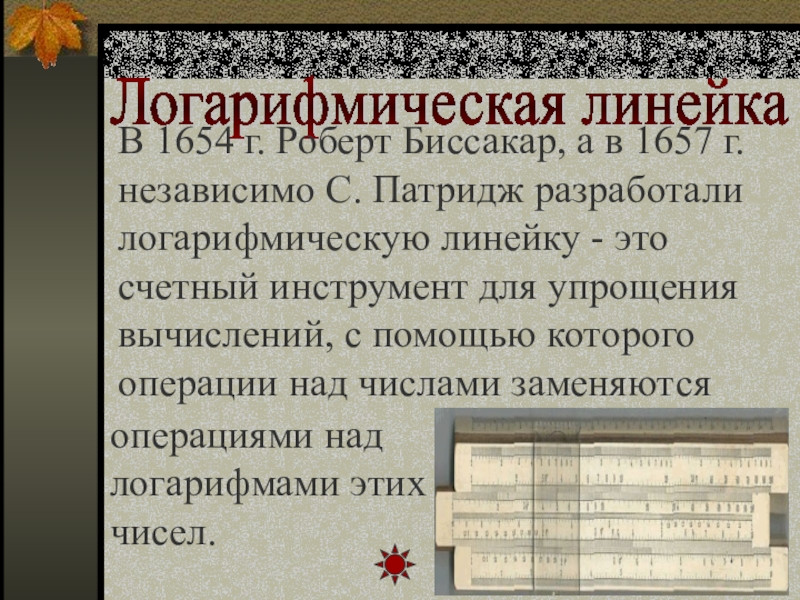
- 15. Логарифмическая линейка В 1654 г. Роберт Биссакар,
- 16. Логарифмическая линейка состоит из 3х частей:1)самой линейки:
- 17. Шкалы логарифмической линейки:1)шкала кубов-самая верхняя.2)шкала квадратов3)основная шкала.4)шкала логарифмов.
- 18. Логарифмом числа b по основанию a называется
- 19. Из определения логарифма вытекает следующее тождество:где a - основание логарифма . Loga1=0Logaa=1
- 20. 1. log a bc = log a
- 21. 1. log a bc = log a
- 22. 2.log a b/c = log a b
- 23. 1) alog ab=b, по основному логарифмическому
- 24. 4. log a b 2n = 2n
- 25. Логарифмическая функция 1) Определение 2) Свойства
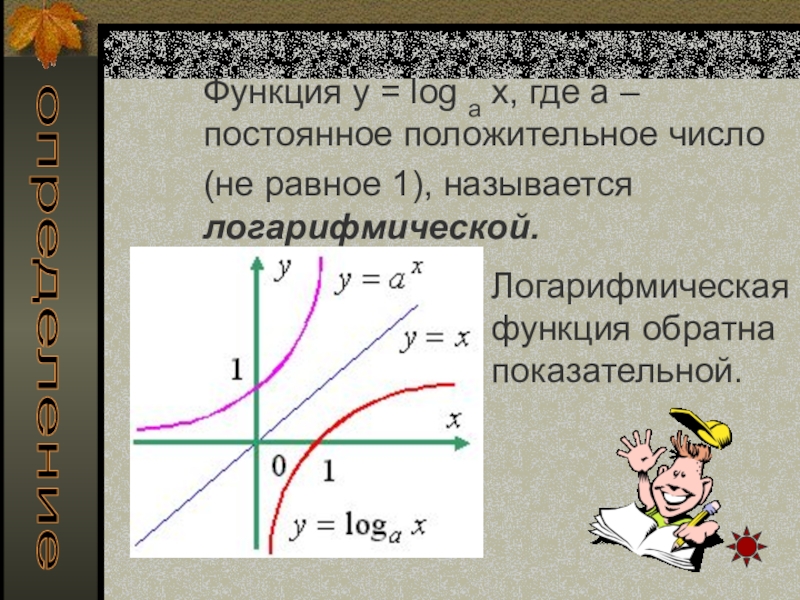
- 26. Функция y = log a x, где а – постоянное положительное
- 27. 1. Область определения логарифмической функции – множество всех положительных
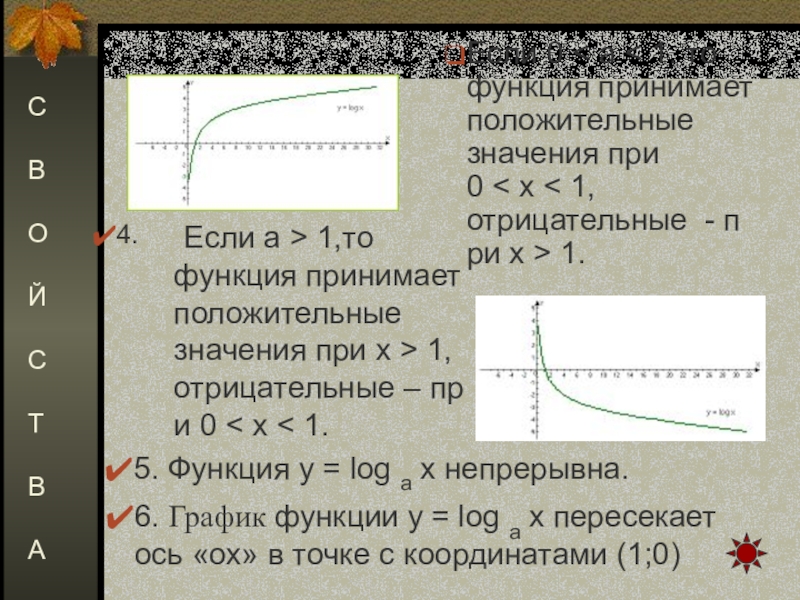
- 28. Если а > 1,то функция принимает положительные значения при x > 1, отрицательные – при 0
- 29. Логарифмические уравнения Логарифмическим уравнением называется уравнение, в
- 30. 5. Переход к логарифму по новому основанию.Методы
- 31. Метод, основанный на определении логарифма.1.Решить уравнение log1/5log5
- 32. Метод, использующий монотонность логарифмической функции. Все корни последнего
- 33. Решение:Так как D(loga)=R+ , то х-5>0 и
- 34. Замечание. Переход от равенства logaa=logab к равенству
- 35. Применение основного логарифмического тождества.Решить уравнение log2(9-2x)=10lg(3-x)Решение: ОДЗ
- 36. Введение нового неизвестного.Решить уравнение lg2x-3lgx=lg(x2)-4Решение: ОДЗ данного
- 37. Переход к логарифму по новому основанию.Решить уравнение
- 38. Логарифмические неравенства Примеры решения
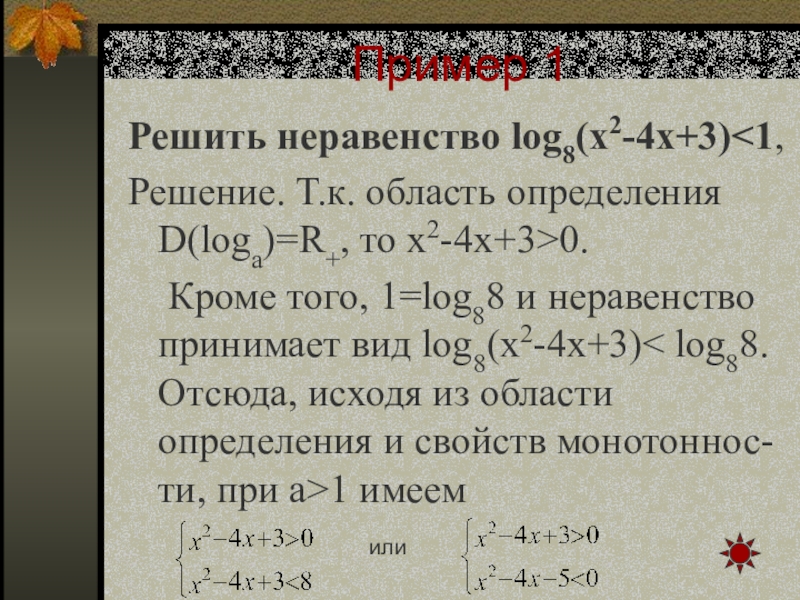
- 39. Пример 1Решить неравенство log8(x2-4x+3)0. Кроме того, 1=log88
- 40. Ответ: x∈(-1:1)∨(3:5) Каждое неравенство решаем методом интервалов:1)x2-4x+3>0, (x-1)(x-3)>0, т.е. x32) x2-4x-5
- 41. Пример 2log 2 (x-1) > 2Правая часть
Слайд 2Содержание:
Логарифм
2.Логарифмическая функция
3.Логарифмические уравнения
4.Логарифмические неравенства
Слайд 3
Определение
логарифма
Свойства логарифмов
ЛОГАРИФМЫ
История
логарифма
Логарифмическая линейка
Применение
логарифмов
Слайд 4История логарифма
Логарифмы были изобретены Джоном Непером (1550-1617), опубликованы им в
Название введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”.
Независимо от него пришел к откры-тию логарифмов Йост Бюрги (1552-1632), который опубликовал свои таблицы в 1620 году.
Слайд 5Логарифмы с основанием e ввел учитель математики Спейдел.
Слово основание заимствовано
Глагол “логарифмировать” появился в 19 веке у Коппе.
Слайд 6Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов.
Прингсхейм обозначал логарифм натурального числа через ln.
Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).
Слайд 7
После появления первых таблиц появились таблицы, содержащие числа от 1 до
Первая таблица десятичных логарифмов опубликована в 1617 году Г.Бригсом.
Слайд 8В течение более чем трех столетий все сложные вычисления выполнялись с
Использование логарифмов позволило астрономам успешно справиться с вычислениями, которые были необходимы для применения законов Ньютона
Слайд 9Период полураспада вещества.
λ = ln2/T
T1/2 = λ-1ln2.
λ-постоянная распада
Применение
Слайд 10Коэффициент звукоизоляции.
Δ L = 10lg(I2/I1), дБ
I1 - сила звука, падающего
Слайд 11Логарифм в природе
В устройстве уха можно заметить орган, который называется улиткой.
Этот
Слайд 12Первым ученым, открывшим эту кривую, был Р.Декарт.
Затем свойства этой спирали были
В логарифмической спирали углу поворота пропорционален логарифм расстояния от полюса до точки кривой. Спираль пересекает все прямые, проходящие через полюс, под одним и тем же углом.
Слайд 13В 1846 г. физиолог Вебер установил зависимость между ощущением и раздражением,
В 1860г. Фехнер сформулировал общий психофизический закон
Вебера-Фехнера: S=klg ,где
S-ощущение;
J0-первоначальное раздражение;
J-последующее раздражение;
K-коэффициент пропорциональности.
Логарифм в психофизике
Слайд 14Логарифмы в музыке.
Величина какого-либо интервала в долях этого тона выражается формулой:
,
f0-частота звука «до»;
fc-частота любого другого звука.
Слайд 15Логарифмическая линейка
В 1654 г. Роберт Биссакар, а в 1657 г.
операциями над логарифмами этих чисел.
Слайд 16 Логарифмическая линейка состоит из 3х частей:
1)самой линейки: корпуса линейки с нанесенными
2)движка- подвижной части,- скользящего в желобке корпуса линейки;
3)бегунка, состоящего из вделанного в металлическую рамку стеклышка. Посредине стеклышка нанесена тонкая визирная линия.
Слайд 17Шкалы логарифмической линейки:
1)шкала кубов-самая верхняя.
2)шкала квадратов
3)основная шкала.
4)шкала логарифмов.
Слайд 18 Логарифмом числа b по основанию a называется показатель степени x, в
Запись log a b= x равнозначно записи ax= b.
Определение логарифма
Примеры. log 2 8= 3, так как 23 = 8; log ½ 16= -4, так как (1/2) –4 =16
Слайд 19 Из определения логарифма вытекает следующее тождество:
где a - основание
Loga1=0
Logaa=1
Слайд 20 1. log a bc = log a b + log a
2.log a b/c = log a b – log a c
3. log a b r = r log a b
Свойства логарифмов
Слайд 211. log a bc = log a b + log a
1) a log ab = b, a log ac = c , по основному логарифмическому тождеству
2) a log a b + log a c =bc
3) log a b + log a c = log a bc,
по определению логарифма
Слайд 222.log a b/c = log a b – log a c
1)a log a b = b, a log a c =c, по
основному логарифмическому
тождеству
2) a log a b - log a c = b/c
3) log a b –log a c = log a b/c, по
определению логарифма
Слайд 231) alog ab=b, по основному логарифмическому тождеству 2) a r log a
3. log a b r = r log a b
Слайд 244. log a b 2n = 2n log a ⎜b ⎜,
Слайд 26Функция y = log a x, где а – постоянное положительное число
(не равное 1),
Логарифмическая функция обратна показательной.
определение
Слайд 271. Область определения логарифмической функции – множество всех положительных чисел.( D∈( 0; +∞
Свойства
2. Множество значений логарифмической функции – множество R+ всех действительных чисел .
Логарифмическая функция y = log a x является возрастающей , если a > 1.
Если 0 < a < 1, то функция убывающая.
3.
Слайд 28 Если а > 1,то функция принимает положительные значения при x > 1, отрицательные – при 0
6. График функции y = log a x пересекает ось «ох» в точке с координатами (1;0)
С
В
О
Й
С
Т
В
А
5. Функция y = log a x непрерывна.
Если 0 < a < 1, то функция принимает положительные значения при 0 < x < 1, отрицательные - при x > 1.
4.
Слайд 29Логарифмические уравнения
Логарифмическим уравнением называется уравнение, в котором неизвестное находится под
Простейшим логарифмическим уравнением является уравнение вида: loga ƒ(x)=b,
где a>0, a≠1, ƒ(x)>0.
Это уравнение равносильно уравнению ƒ(x)=ab
В случае, когда ƒ (x)=x, x>0,
логарифмическое уравнение имеет решение x=ab.
Слайд 305. Переход к логарифму по новому основанию.
Методы решения
1. Метод, основанный
2. Решение с помощью
потенцирования;
3.Применение основного логарифмического тождества;
4. Введение нового неизвестного;
Слайд 31Метод, основанный на определении логарифма.
1.Решить уравнение log1/5log5 =0 Используя
log5 =1,
откуда =51
Следовательно, 5х=25 ,
х=5 .
Проверка
log1/5log5 =log1/5log55=log1/51=0
Ответ: х=5.
Слайд 32Метод, использующий монотонность логарифмической функции.
Все корни последнего уравнения и будут корнями
Уравнение logaƒ(x)=logag(x) можно решить по схеме :
найти ОДЗ этого уравнения ;
2)решить на ОДЗ этого уравнения равносильное ему уравнение ƒ(x)=g(x).
Слайд 33Решение:Так как D(loga)=R+ , то х-5>0 и x+7>0.
Имеем х-5>0; x>5; x+7>0
Исходное уравнение можно представить
в виде:
Пример. Решить уравнение:
lg8-lg(x-5)=lg2-lg
Возведя обе части в квадрат, получим 16(х+7)=х2-10х+25.
Решение этого квадратного уравнения х1=-3, х2=29.
Число х=-3 не входит в ОДЗ. Следовательно, х=29.
Ответ: х=29.
Это уравнение при x>5 равносильно
Слайд 34Замечание.
Переход от равенства logaa=logab
к равенству а=b называется потенцированием
Слайд 35Применение основного
логарифмического тождества.
Решить уравнение log2(9-2x)=10lg(3-x)
Решение: ОДЗ находится решением системы:
Применив в
Используя определение логарифма, имеем 9-2х=23-х ; 9-2х=8/2x
Полагая 2х=y, y>0 получаем 9-y= 8/y
y2-9y+8=0
y ≠0, откуда y1 =1, y2 =8
Следовательно , 2х=1 или 2х=8 , т.е. х1=0,х2=3.
Но х2=3-посторонний корень, т.к. не входит в ОДЗ.
Ответ: 0
Слайд 36Введение нового неизвестного.
Решить уравнение lg2x-3lgx=lg(x2)-4
Решение:
ОДЗ данного уравнения х>0, поэтому
lg(x2)=2lgx,
Тогда уравнение примет вид y2-5y+4=0
Его решения y1=1 , y2=4
Откуда имеем
Оба корня входят в ОДЗ.
Ответ: 10;10000.
Слайд 37 Переход к логарифму по новому основанию.
Решить уравнение log2(x2-1)=log1/2(x-1)
Решение: Найдём ОДЗ
x2-1>0 ⇔(x-1)(x+1) >0 ⇔ x<-1или x>1.
Преобразуем выражение правой части уравнения к логарифму по основанию 2. Используя формулу перехода, получим
В результате имеем уравнение log2(x2-1)=-log2(x-1)
Отсюда, используя свойства логарифмической функции, получим
x2-1=(x-1)-1⇔x2-1=1/x-1 Преобразования дают (х2-1)(х-1)=1<=>
х3-х2-х+1=1 , т.е. х(х2-х-1)=0.
Решая его получим х1=0,
Из найденных трёх значений
лишь входит в ОДЗ, т.к. он больше 1
Ответ:
Слайд 39Пример 1
Решить неравенство log8(x2-4x+3)0.
Кроме
или
Слайд 40Ответ:
x∈(-1:1)∨(3:5)
Каждое неравенство решаем методом интервалов:
1)x2-4x+3>0, (x-1)(x-3)>0,
т.е. x
2) x2-4x-5<0, (x+1)(x-5)<0 Совмещая промежутки, имеем:
т.е. –1
x∈(-1:1)∨(3:5)
Слайд 41Пример 2
log 2 (x-1) > 2
Правая часть данного неравенства имеет смысл
Так как логарифмическая функция с основанием 2 возрастающая, то неравенство при условии x – 1 > 0 выполняется, если x – 1 > 4.
Таким образом, данное неравенство равносильно системе неравенств:
x ∈ (5;+∞).
Ответ: x ∈ (5;+∞).