- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Неравенства (8 класс)
Содержание
- 1. Презентация по математике Неравенства (8 класс)
- 2. Актуальность проектаДанная тема выбрана мной, исходя из
- 3. Цель исследования: изучить основные способы
- 4. Исторические сведения о возникновении неравенств Архимед (III в. до н.э.)Папп АлександрийскийЕвклид
- 5. Ученые, впервые использовавшие знаки строгих неравенств «»,
- 6. НеравенстваНеравенствами называют выражения вида а ≤ в
- 7. Вспомним
- 8. Основные виды преобразований неравенствЕсли к обеим
- 9. Основные виды решения линейных неравенств
- 10. Преобразование неравенства 5х – 5 < 2х – 16 .
- 11. Решение линейных неравенств Решить неравенство:
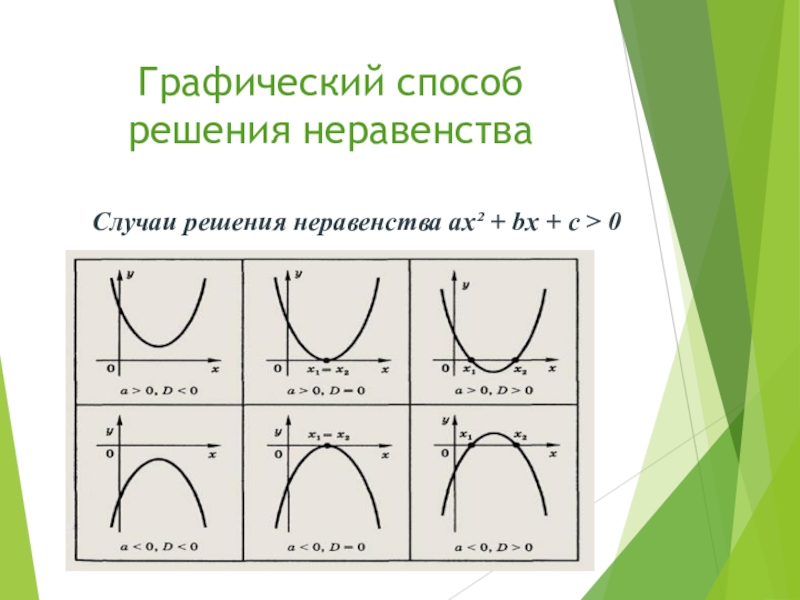
- 12. Графический способ решения неравенстваСлучаи решения неравенства ax² + bx + c > 0
- 13. Решить графически неравенствоРешить графически неравенство х²+5х-6≤0Решение:
- 14. Решение неравенств методом интервалов 1. (x –
- 15. Применение неравенств
- 16. ЗаключениеЯ рассмотрела способы решения неравенств линейных и
- 17. Спасибо за внимание
Актуальность проектаДанная тема выбрана мной, исходя из сложности изучения решения неравенств. Неравенства применяются как при решении алгебраических, так и геометрических задач. Для успешного решения применяется алгоритм решения неравенств, которым я хочу овладеть. Материал, связанный с неравенствами,
Слайд 1Муниципальное общеобразовательное учреждение «Килачевская средняя общеобразовательная школа»
Неравенства
Проект ученицы 8 «а» класса
Делевин Екатерины Евгеньевны
Руководитель проекта
Шарапова Галина Геннадьевна
2019 год
Слайд 2Актуальность проекта
Данная тема выбрана мной, исходя из сложности изучения решения неравенств.
Неравенства применяются как при решении алгебраических, так и геометрических задач.
Для успешного решения применяется алгоритм решения неравенств, которым я хочу овладеть. Материал, связанный с неравенствами, составляет значительную часть школьного курса математики. Например, неравенства используются при изучении свойств функции, решении текстовых задач, в которых построение математической модели приводит к неравенству или системе неравенств.
Знания, умения, навыки решения неравенств будут необходимы мне при подготовке к ОГЭ.
Для успешного решения применяется алгоритм решения неравенств, которым я хочу овладеть. Материал, связанный с неравенствами, составляет значительную часть школьного курса математики. Например, неравенства используются при изучении свойств функции, решении текстовых задач, в которых построение математической модели приводит к неравенству или системе неравенств.
Знания, умения, навыки решения неравенств будут необходимы мне при подготовке к ОГЭ.
Слайд 3 Цель исследования: изучить основные способы решения неравенств, рассматриваемые в основной школе. Задачи
исследования:
1.Представить исторические сведения о возникновении в школьном курсе линии неравенств.
2.Выделить основные типы преобразований неравенств.
3.Применить основные способы решения неравенств.
Объект исследования: процесс решения неравенств основной школы.
Предмет исследования: линейные и квадратные неравенства.
Слайд 4Исторические сведения о возникновении неравенств
Архимед (III в. до н.э.)
Папп Александрийский
Евклид
Слайд 5Ученые, впервые использовавшие знаки строгих неравенств «», и нестрогих
неравенств «≤ » и « ≥ »
Томас Гарриот
Пьер Бюге
Слайд 6Неравенства
Неравенствами называют выражения вида
а ≤ в , а≥ в или
а ‹ в , а › в (нестрогие, строгие), где а и в могут быть числами или функциями.
Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в верное числовое неравенство.
Решить неравенство это значить найти все его решения или установить что их нет.
Два неравенства называются равносильными, если их множества решений совпадают.
Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в верное числовое неравенство.
Решить неравенство это значить найти все его решения или установить что их нет.
Два неравенства называются равносильными, если их множества решений совпадают.
Слайд 8 Основные виды преобразований неравенств
Если к обеим частям неравенства f(х) >
g(х) прибавить одно и то же число d, то получим неравенство f(х) + d > g(х) + d, равносильное исходному.
Если какое-либо слагаемое перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Если обе части неравенства f(х) > g(х) умножить на одно и то же положительное число d, то получим неравенство f(х)∙d > g(х)∙d, равносильное данному.
Если обе части неравенства f(х) > g(х) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(х)∙d< g(х)∙d, равносильное данному.
Если какое-либо слагаемое перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Если обе части неравенства f(х) > g(х) умножить на одно и то же положительное число d, то получим неравенство f(х)∙d > g(х)∙d, равносильное данному.
Если обе части неравенства f(х) > g(х) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(х)∙d< g(х)∙d, равносильное данному.
Слайд 11 Решение линейных неравенств
Решить неравенство: 3(х – 2) – 4(х
+ 1) < 2(х – 3) – 2
Упростим левую и правую части неравенства:
3х – 6 – 4х < 2х – 6 – 2
–х – 10 < 2х – 6 – 2
–3х < 2
х> – 2/3
Множество чисел х, удовлетворяющих конечному неравенству, на числовой оси изображается лучом, а точка х = –2/3 не принадлежит этому лучу (отмечается не закрашенной точкой на числовом луче), сам луч изображен штриховкой.
Ответ: х∈(– 23 ;+∞).
Упростим левую и правую части неравенства:
3х – 6 – 4х < 2х – 6 – 2
–х – 10 < 2х – 6 – 2
–3х < 2
х> – 2/3
Множество чисел х, удовлетворяющих конечному неравенству, на числовой оси изображается лучом, а точка х = –2/3 не принадлежит этому лучу (отмечается не закрашенной точкой на числовом луче), сам луч изображен штриховкой.
Ответ: х∈(– 23 ;+∞).
Слайд 13Решить графически неравенство
Решить графически неравенство х²+5х-6≤0
Решение: рассмотрим у = х²+5х-6,
это квадратичная функция, графиком является парабола, т.к. а=1, то ветви направлены вверх.
у
+ +
-6 1 x
Ответ: [-6;1]
Слайд 14Решение неравенств методом интервалов
1. (x – 6)(x + 3) ≥ 0
1.
Найдем корни уравнения (x – 6)(x + 3) = 0
x – 6 = 0 или x + 3 = 0
x = 6 x = - 3
2. Отметим корни на числовой оси.
+ - +
-3 6 х
Неравенству соответствуют промежутки со знаком «+»
3. Ответ: (–∞; –3] U [6; +∞).
x – 6 = 0 или x + 3 = 0
x = 6 x = - 3
2. Отметим корни на числовой оси.
+ - +
-3 6 х
Неравенству соответствуют промежутки со знаком «+»
3. Ответ: (–∞; –3] U [6; +∞).
Слайд 16Заключение
Я рассмотрела способы решения неравенств линейных и квадратных.
Научилась решать квадратные
неравенства графическим способом и методом интервалов, а также записывать решение неравенства с помощью числовых промежутков.
Я проанализировала как используются неравенства, и какое применение находят в нашей жизни.
Поняла, что неравенства играют важную роль: каждый день мы что-то сравниваем, определяем форму необходимых нам предметов, приборов и механизмов. Неравенства просто необходимы при проектировании зданий, прокладывании дорог, они помогают в построении планов и схем, делают наш быт и повседневность проще, легче и удобней.
Неравенства – это интересно!
Я проанализировала как используются неравенства, и какое применение находят в нашей жизни.
Поняла, что неравенства играют важную роль: каждый день мы что-то сравниваем, определяем форму необходимых нам предметов, приборов и механизмов. Неравенства просто необходимы при проектировании зданий, прокладывании дорог, они помогают в построении планов и схем, делают наш быт и повседневность проще, легче и удобней.
Неравенства – это интересно!