2017 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему:Первообразная и интеграл (1 курс)
Содержание
- 1. Презентация по математике на тему:Первообразная и интеграл (1 курс)
- 2. По заданным производным найдите исходные функциидифференцированиеинтегрирование
- 3. Обозначения: f(x)-функция;
- 4. Найдите производные функций:совокупность первообразных
- 5. Совокупность всех первообразных F(x)+c для функции f(x)
- 6. Свойства неопределенного интеграла1)2)
- 7. Определение:Пусть дана положительная функция f(x), определенная на
- 8. Обозначение:«интеграл от a до bэф от икс дэ икс»
- 9. Формула Ньютона - Лейбница
- 10. Слайд 10
- 11. Слайд 11
- 12. Пример 1.Вычислить определённый интеграл:=Решение:
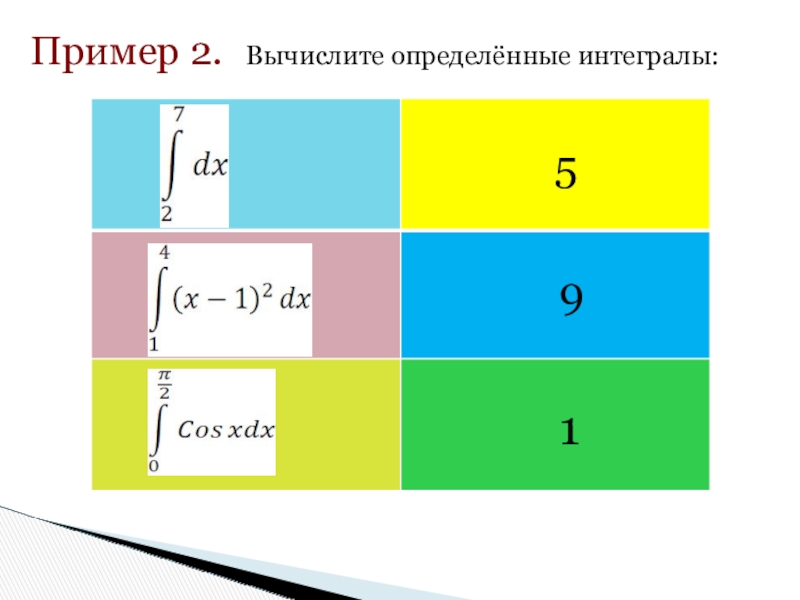
- 13. Пример 2.Вычислите определённые интегралы:591
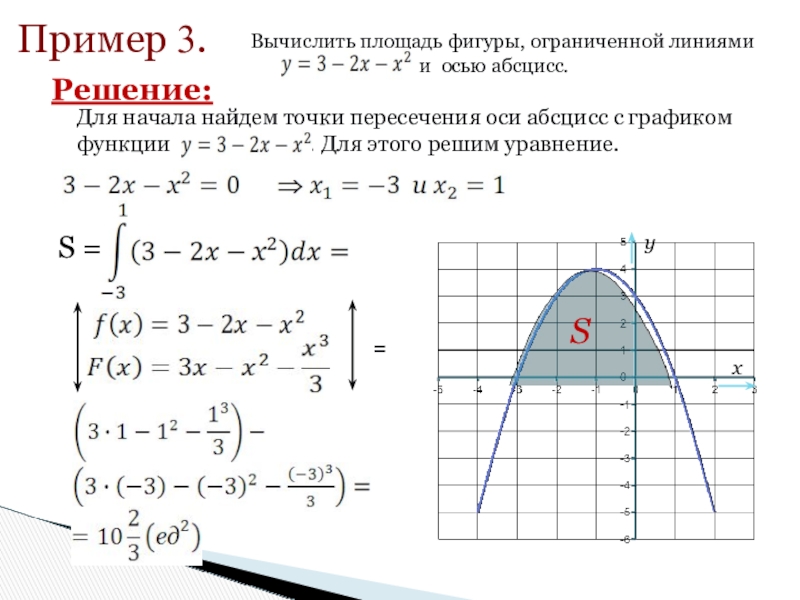
- 14. Пример 3. =Решение: S =
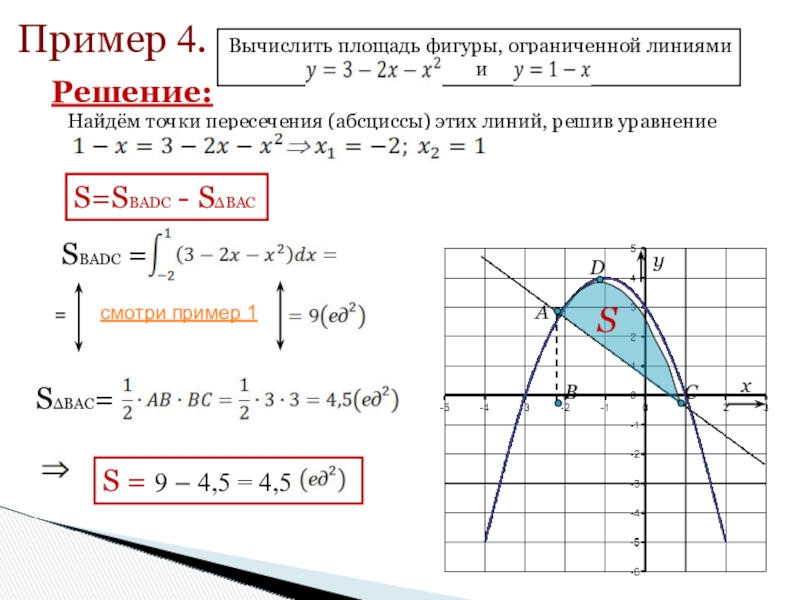
- 15. Пример 4.Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=SBADC - SΔBACSBADC == SΔBAC=Решение:
- 16. Пример 1.Вычислить определённый интеграл:=Решение: пример 4
- 17. Немного истории «Интеграл» - латинское слово integro
- 18. Немного истории Знак ∫ - стилизованная буква
- 19. Лейбниц Готфрид Вильгельм (1646-1716) « Общее
- 20. Исаак Ньютон (1643-1727)Разумом он превосходил род человеческий.
- 21. Применение интеграла Площадь фигурыОбъем тела вращенияРабота электрического зарядаРабота переменной силыЦентр массФормула энергии заряженного конденсатора
- 22. Спасибо за урок!!!Что быстрее всего ? –
По заданным производным найдите исходные функциидифференцированиеинтегрирование
Слайд 1ПЕРВООБРАЗНАЯ.
ИНТЕГРАЛ.
Преподаватель:
Косян Анаит Георгиевна
ГБПОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ГУМАНИТАРНЫЙ КОЛЛЕДЖ»
Богучар –
Слайд 3Обозначения: f(x)-функция;
F(x)-первообразная
ПЕРВООБРАЗНАЯ
Функция F называется первообразной для функции f, если выполняется условие
Слайд 5Совокупность всех первообразных F(x)+c
для функции f(x) называется неопределенным интегралом и
обозначается
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
где f(x) – подинтегральная функция,
f(x)dx – подинтегральное выражение,
с – постоянная интегрирования.
Слайд 7
Определение:
Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b].
Интегралом от
функции f(x) на [a;b] называется площадь её криволинейной трапеции.
![Определение:Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b].Интегралом от функции f(x) на [a;b] называется площадь](/img/thumbs/027ee16246e6bf7e97dbc7fb24d03a3d-800x.jpg "Презентация по математике на тему:Первообразная и интеграл (1 курс) Определение:Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b].Интегралом от")
Слайд 15
Пример 4.
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC -
SΔBAC
SBADC =
=
SΔBAC=
Решение:
Слайд 17Немного истории
«Интеграл» - латинское слово integro – “восстанавливать” или integer –
“целый”.
Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным.
Впервые это слово употребил в печати швецкий ученый Я. Бернулли (1690 г.).
Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным.
Впервые это слово употребил в печати швецкий ученый Я. Бернулли (1690 г.).
Слайд 18Немного истории
Знак ∫ - стилизованная буква S от латинского слова summa
– “сумма”. Впервые появился у Г.В. Лейбница в 1686 году.
Слайд 19Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков представляет чудесное пособие,
так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»
Лейбниц
Лейбниц
Слайд 21Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Центр масс
Формула
энергии заряженного конденсатора
Слайд 22Спасибо за урок!!!
Что быстрее всего ? – Ум.
Что мудрее всего ?
– Время.
Что приятнее всего ? –
Достичь желаемого. Фалес Милетский
Что приятнее всего ? –
Достичь желаемого. Фалес Милетский
