Мария Сергеевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему:Метод интервалов (8 класс)
Содержание
- 1. Презентация по математике на тему:Метод интервалов (8 класс)
- 2. Методическая разработка урока Цели урока:-
- 3. Ход урокаI.Организационный моментII. Устная работаIII. Изучение нового материалаIѴ. Закрепление материалаѴ. Рефлексия.ѴI. Итог урока, домашнее задание.
- 4. Устная работаПовторение свойств функций : y=f(x).2.
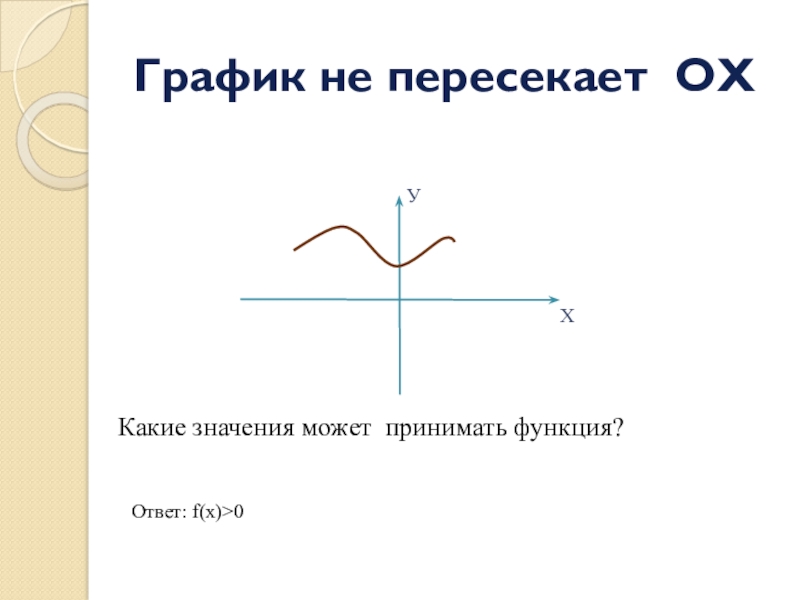
- 5. Ответ: f(x)>0График не пересекает ОХКакие значения может принимать функция? ХУ
- 6. График функции y=f(x) пересекает ОХ Какие
- 7. График функции y=f(x) пересекает ось
- 8. Линия подошла к ОХ, стала на неё
- 9. Линия разорвалась в Х4 и появилась в нижней полуплоскостиВопрос: Назвать интервалы знакопостоянстваОтвет:f(x)>0 при X
- 10. Вопрос: Когда происходит смена знака функции?Ответ: Если
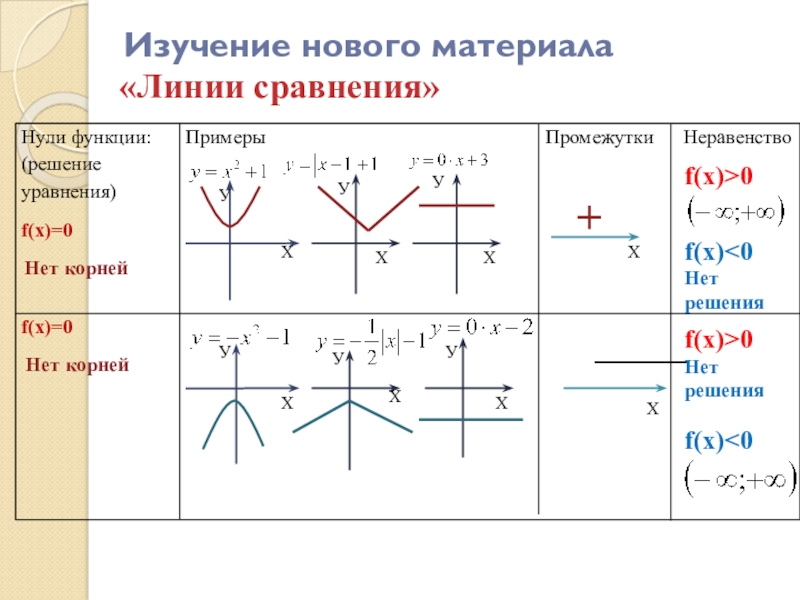
- 11. Изучение нового материала «Линии сравнения»УХУХХУУУУХХХ +ХХf(x)>0f(x)>0f(x)
- 12. 2)Нули функции: (решение уравнения) f(x)=0Один корень Х=Х1+Х1Х1ХУУУУХХХХ1Х1Х1Х1+++f(x)>0f(x)
- 13. 2)Нули функции: (решение уравнения) f(x)=0Два корня Х=Х1 Х= Х2+Х1Х1ХУУХХХ1Х1+f(x)>0f(x)
- 14. 2)Нули функции: (решение уравнения) f(x)=0
- 15. 2. Сформулировать алгоритм решения неравенств методом интервалов,
- 16. 3. Образец решения неравенств методом интервалов:-2
- 17. Рефлексия, итог урока.Обучающая самостоятельная работа.Что мы
- 18. Обучающая самостоятельная работа II Вариант1.2.3.4.5.1.2.3.4.5.I Вариант
- 19. Итог урока, домашнее задание:Д/З П.42№№ 675—677 (2, 4)
Методическая разработка урока Цели урока:- Содействовать формированию интеллектуальной, исследовательской , культуры учащихся (умению анализировать ,конкретизировать ,творческимыслить ,обобщать полученные знания ,размышлять и рассуждать ) .- Развивать коммуникативные способности учащихся.Задачи урока :- Повторить свойства функций их
Слайд 1Тема урока
Метод интервалов
8 класс . Государственное общеобразовательное
учреждение школа № 457.
Железова
Слайд 2Методическая разработка урока
Цели урока:
- Содействовать формированию интеллектуальной, исследовательской
,
культуры учащихся (умению анализировать ,конкретизировать ,творчески
мыслить ,обобщать полученные знания ,размышлять и рассуждать ) .
- Развивать коммуникативные способности учащихся.
Задачи урока :
- Повторить свойства функций их графики
- Выработать алгоритм решения неравенства методом интервалов
Слайд 3Ход урока
I.Организационный момент
II. Устная работа
III. Изучение нового материала
IѴ. Закрепление материала
Ѵ. Рефлексия.
ѴI.
Итог урока, домашнее задание.
Слайд 4Устная работа
Повторение свойств функций : y=f(x).
2. Слайд –шоу “Путешествие линии
y=f(x)
в прямоугольной системе координат “
в прямоугольной системе координат “
Слайд 6График функции y=f(x)
пересекает ОХ
Какие значения принимает функция слева (справа)
от точки пересечения графика с осью ОХ?
Ответ: f(x)>0 при х X1 У Х
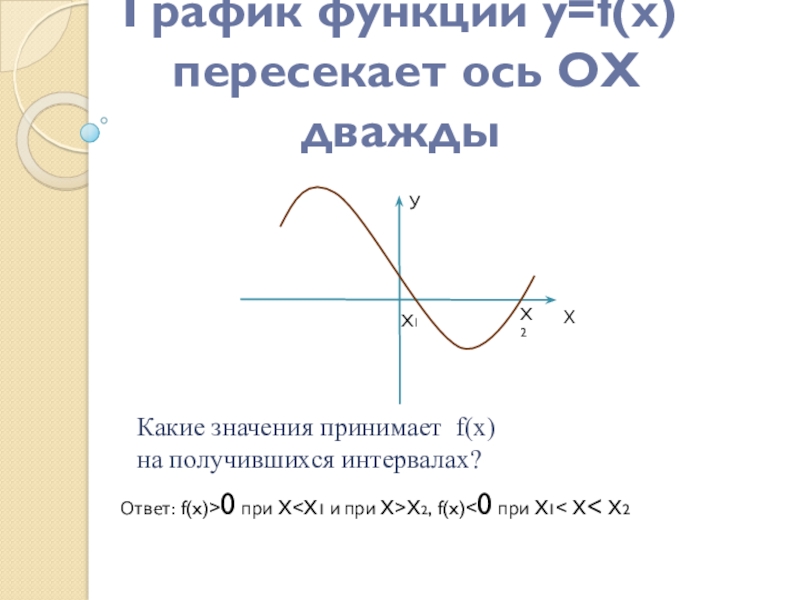
Слайд 7График функции y=f(x)
пересекает ось ОХ дважды
X1
X2
Какие значения принимает f(x)
на получившихся интервалах?
Ответ: f(x)>0 при х У Х
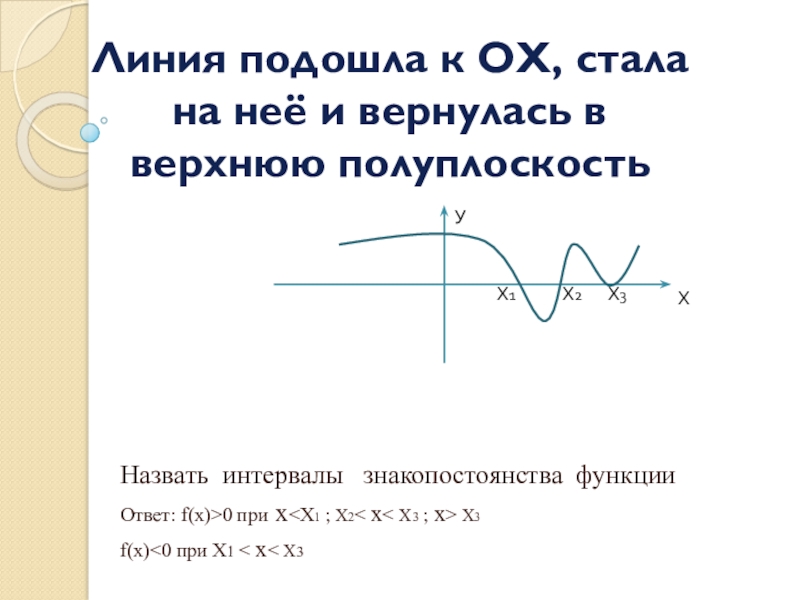
Слайд 8Линия подошла к ОХ, стала на неё и вернулась в верхнюю
полуплоскость
Назвать интервалы знакопостоянства функции
Ответ: f(x)>0 при х<Х1 ; Х2< x< Х3 ; x> Х3
f(x)<0 при Х1 < x< Х3
Х1
Х2
Х3
Х
У
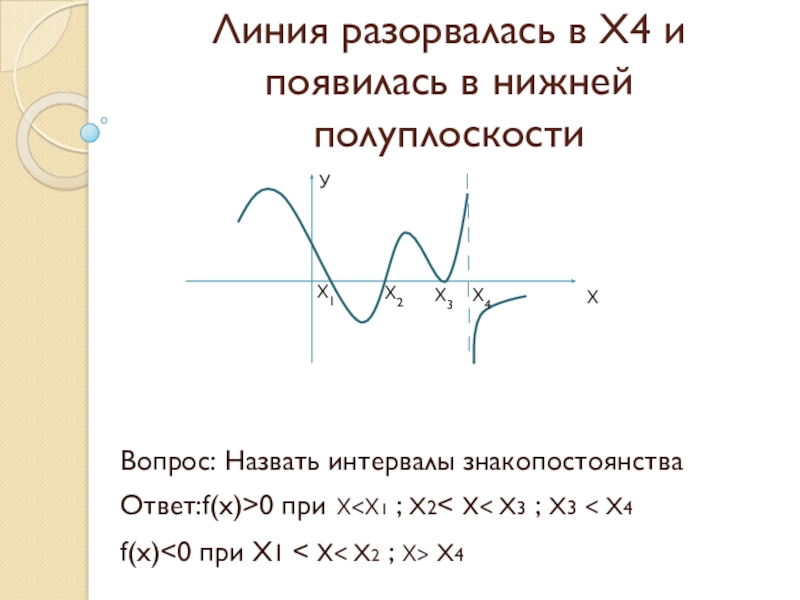
Слайд 9Линия разорвалась в Х4 и появилась в нижней полуплоскости
Вопрос: Назвать интервалы
знакопостоянства
Ответ:f(x)>0 при X<Х1 ; Х2< x< Х3 ; Х3 < Х4
f(x)<0 при Х1 < x< Х2 ; X> Х4
Ответ:f(x)>0 при X<Х1 ; Х2< x< Х3 ; Х3 < Х4
f(x)<0 при Х1 < x< Х2 ; X> Х4
Х1
Х2
Х3
Х4
У
Х
Слайд 10Вопрос: Когда происходит смена знака функции?
Ответ: Если функция пересечет ось ОХ
и перейдет из одной полуплоскости в другую.
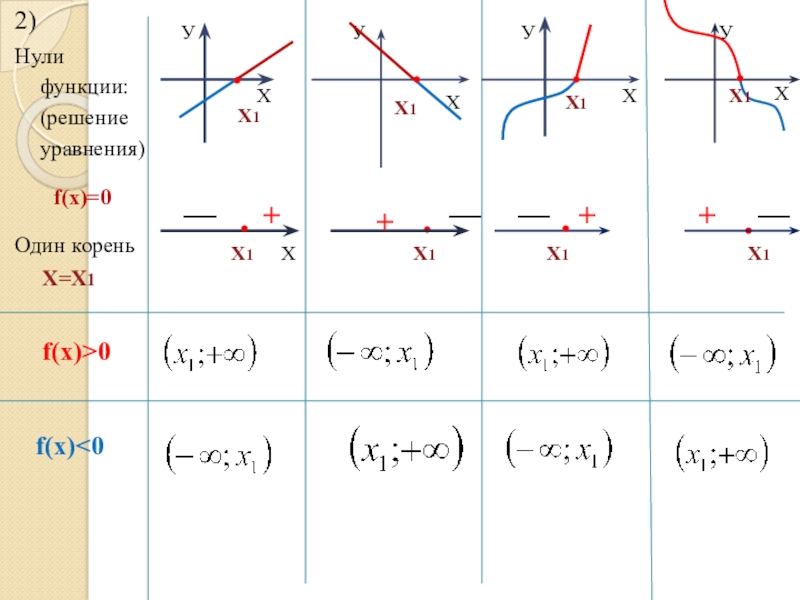
Слайд 122)
Нули функции: (решение уравнения)
f(x)=0
Один корень
Х=Х1
+
Х1
Х1
Х
У
У
У
У
Х
Х
Х
Х1
Х1
Х1
Х1
+
+
+
f(x)>0
f(x)<0
Х1
Х1
Х
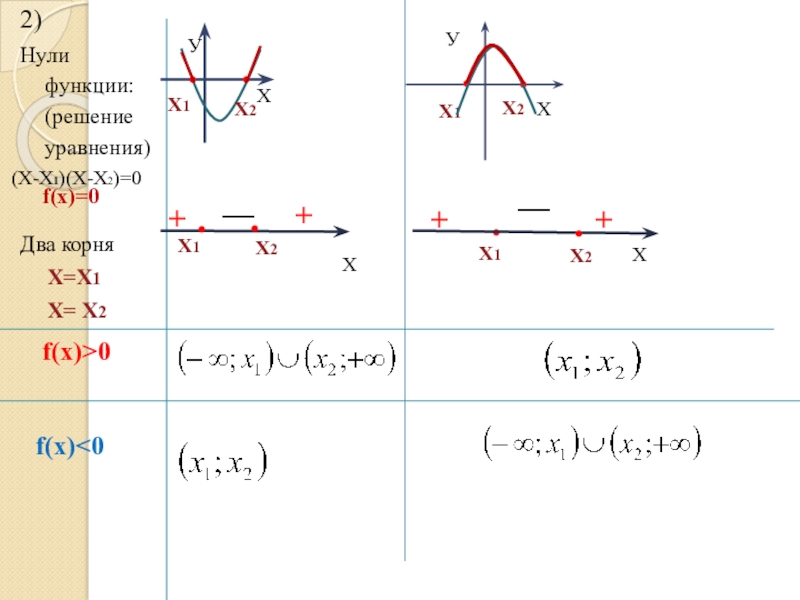
Слайд 132)
Нули функции: (решение уравнения)
f(x)=0
Два корня
Х=Х1
Х= Х2
+
Х1
Х1
Х
У
У
Х
Х
Х1
Х1
+
f(x)>0
f(x)<0
+
Х2
Х2
Х
+
(Х-Х1)(Х-Х2)=0
Х2
Х2
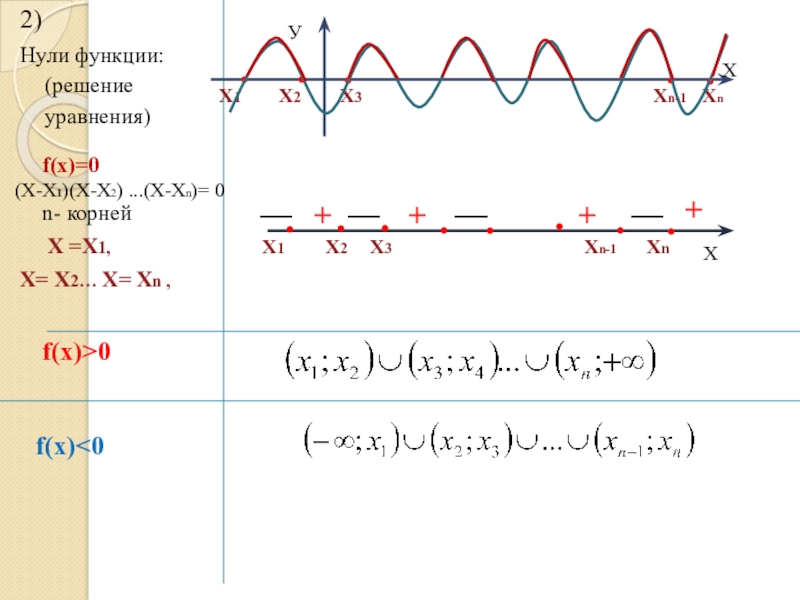
Слайд 142)
Нули функции: (решение уравнения)
f(x)=0
n- корней
Х =Х1,
Х= Х2… Х= Хn ,
Х= Х2… Х= Хn ,
+
Х1
Х3
Х
У
Х1
Х3
+
f(x)>0
f(x)<0
Х2
Хn
Х
+
(Х-Х1)(Х-Х2) ...(Х-Хn)= 0
Х2
Хn
Хn-1
Хn-1
+
Слайд 152. Сформулировать алгоритм решения неравенств методом интервалов, если f(x) - многочлен
А)
Решить уравнение f(x)=0
Б) Найденные корни разместить на ось Х
В) Определить знаки интервалов
Г) Выбрать необходимые интервалы и записать ответ
Б) Найденные корни разместить на ось Х
В) Определить знаки интервалов
Г) Выбрать необходимые интервалы и записать ответ
Слайд 163. Образец решения неравенств методом интервалов:
-2
2 х
.
.
Г)
В) f(3) = 9-4=5>0 f(0) = 0-4= -4<0 f(-3) = 9-4=5>0
А)
Б)
+ +
_
Ответ:
Слайд 17 Рефлексия, итог урока.
Обучающая самостоятельная работа.
Что мы изучали сегодня на уроке?
Что
называется решением системы неравенств?
Что значит решить систему неравенств?
Какие числовые промежутки вы знаете?
Какую оценку ты бы поставил …за работу на уроке?
Что значит решить систему неравенств?
Какие числовые промежутки вы знаете?
Какую оценку ты бы поставил …за работу на уроке?
