- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
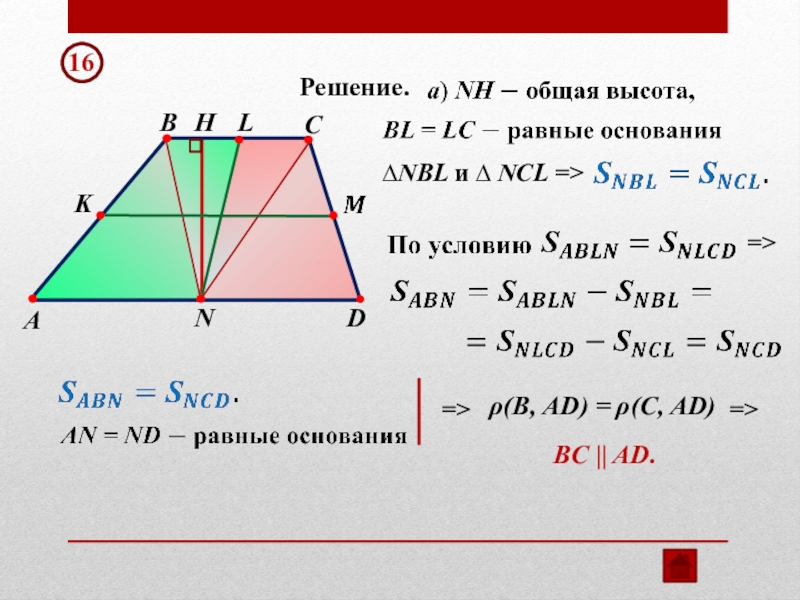
- ОБЖ
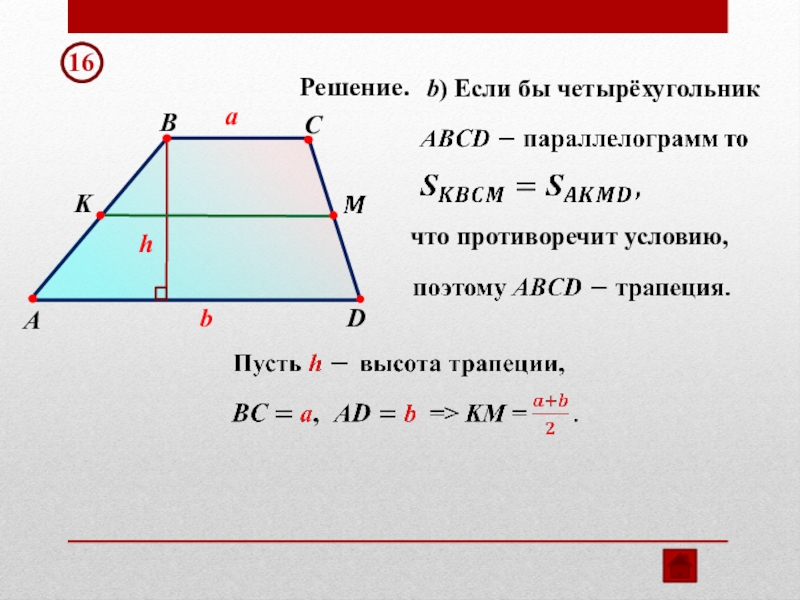
- Обществознание
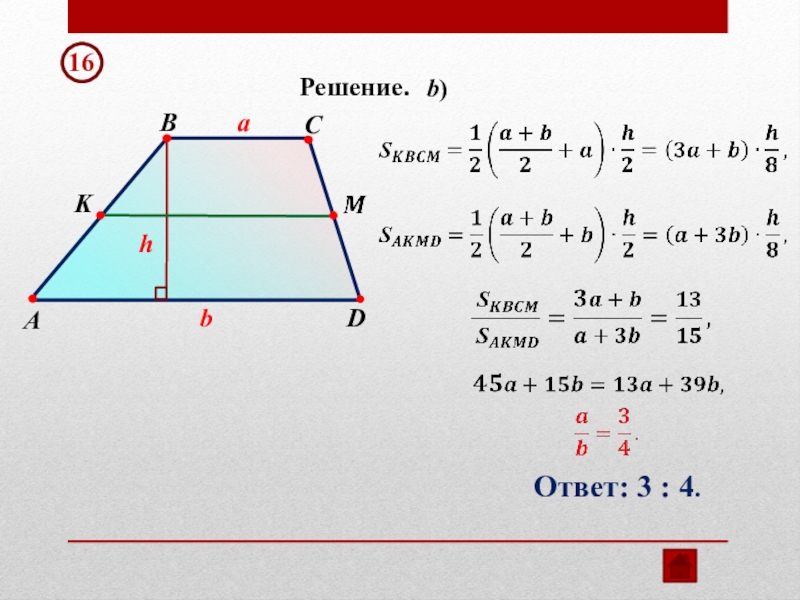
- Окружающий мир
- Педагогика
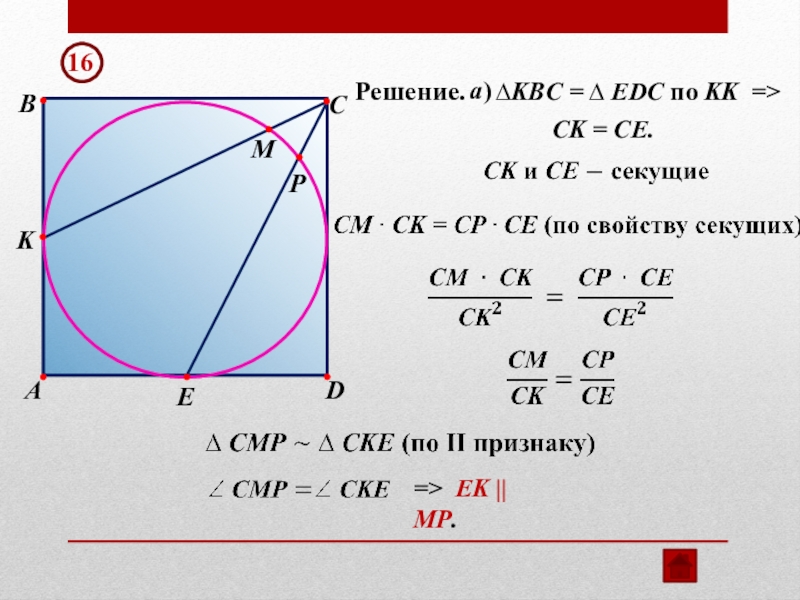
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задания ЕГЭ 2016 года (11 класс)
Содержание
- 1. Презентация по математике на тему Задания ЕГЭ 2016 года (11 класс)
- 2. Содержание
- 3. 13
- 4. Решение. 13
- 5. 13
- 6. Решение. 13
- 7. 13
- 8. Типичные ошибки, допущенные учащимися в заданиях 13:при
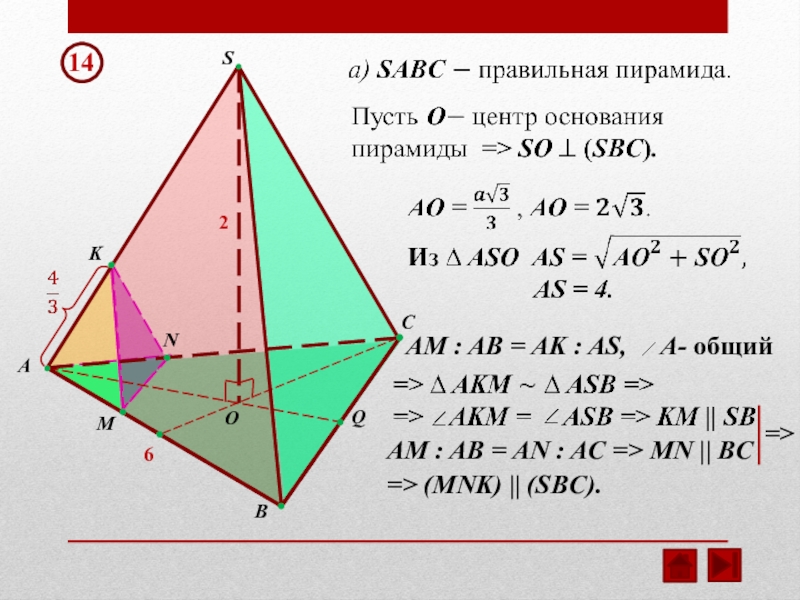
- 9. 14
- 10. NMSСAВKQO26AM : AB = AN : AC => MN || BC=> (MNK) || (SBC). 14
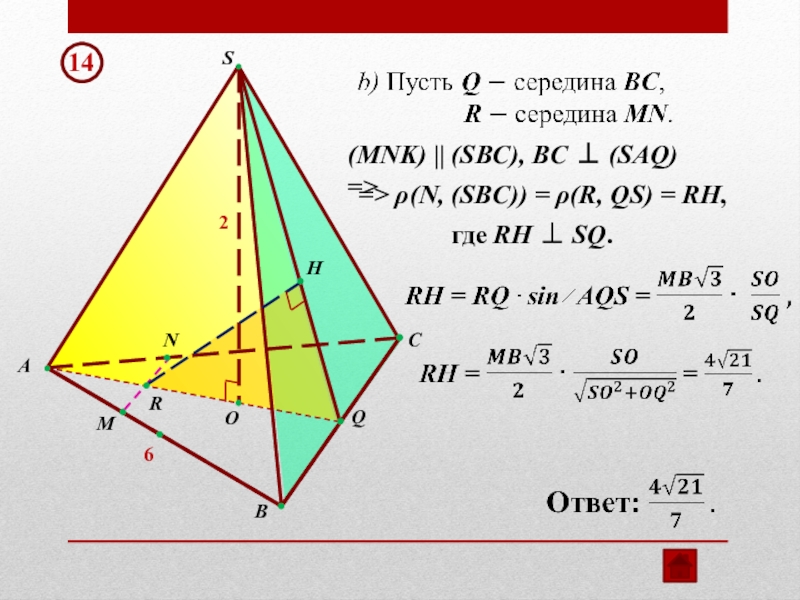
- 11. HNMRSСAВQO26(MNK) || (SBC), BC (SAQ) =>=>
- 12. 14
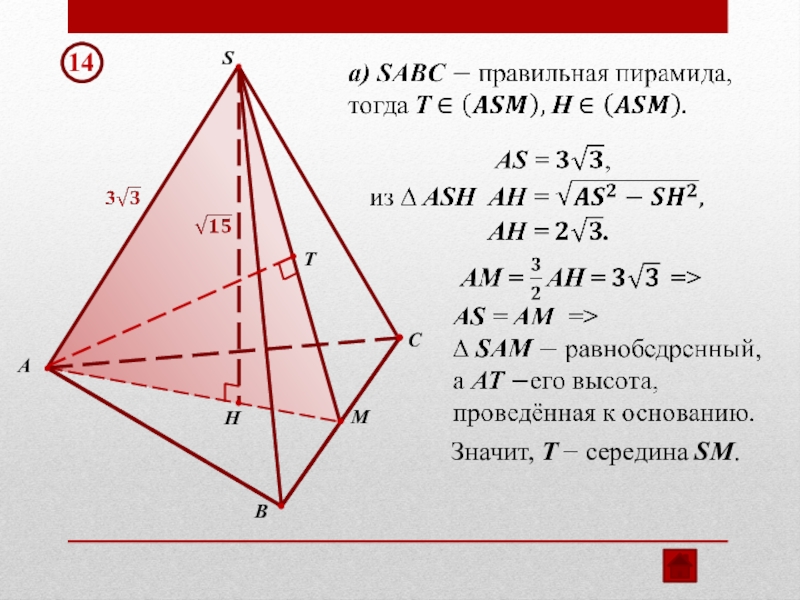
- 13. TSСAВMHЗначит, T − середина SM.14
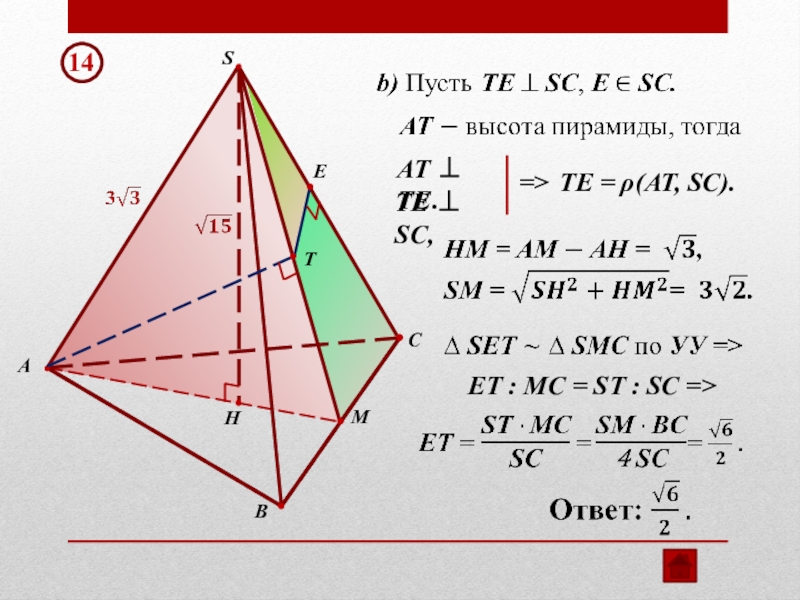
- 14. SСAВMHTEAT TE. TE SC, =>
- 15. 14
- 16. С этими заданиями в 2016 году
- 17. 15
- 18. 15
- 19. 15
- 20. 15Решение.
- 21. Типичные ошибки учащихся, допущенные в заданиях 15:при
- 22. 16
- 23. ABCDKLNHBC || AD. 16
- 24. ABCDKb) Если бы четырёхугольникРешение.hчто противоречит условию,ab16
- 25. ABCDKb)Решение.habОтвет: 3 : 4.16
- 26. 16
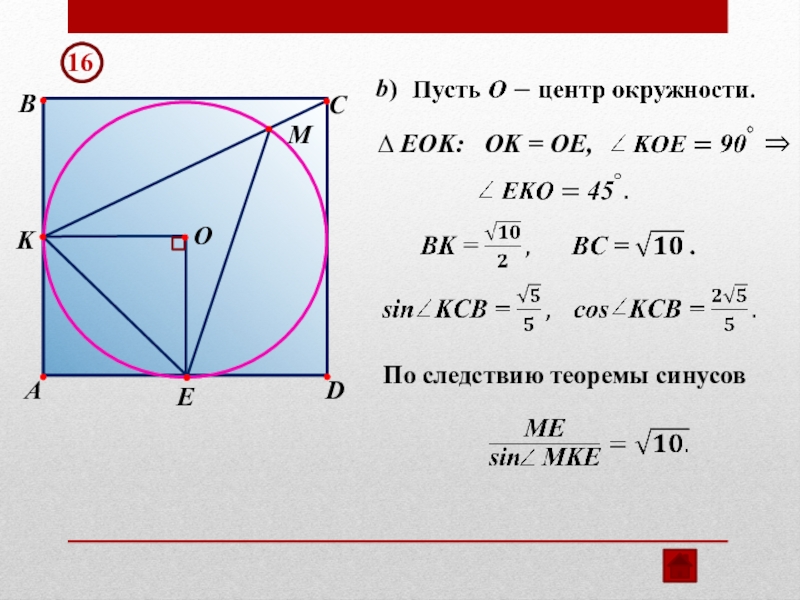
- 27. EKA16 BCMDPCK = CE.
- 28. EKABCMDOПо следствию теоремы синусов16
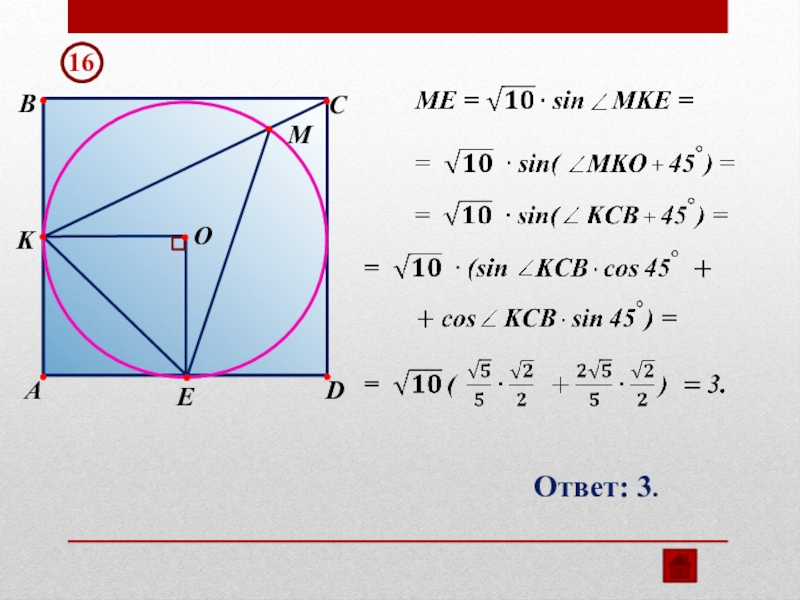
- 29. OEKABCMDОтвет: 3.16
- 30. 16
- 31. Типичные ошибки учащихся, допущенные в заданиях 16:при
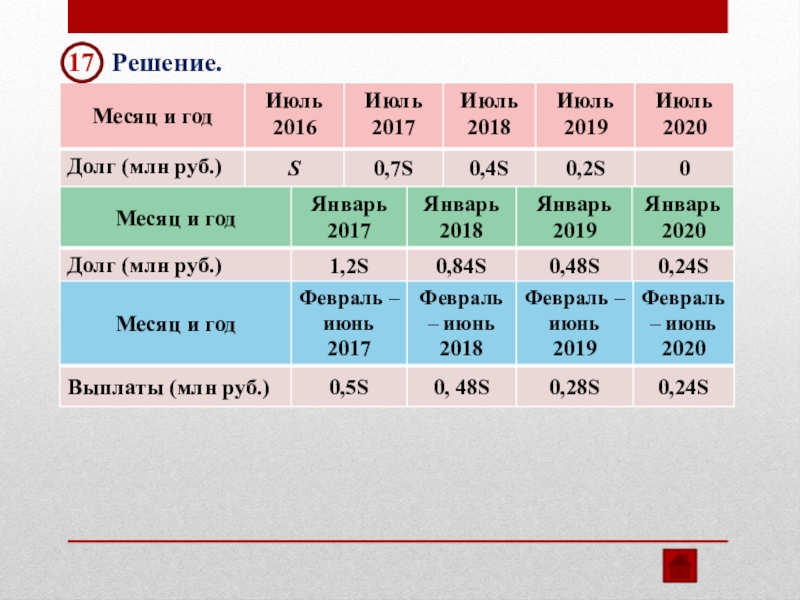
- 32. 17 Найдите
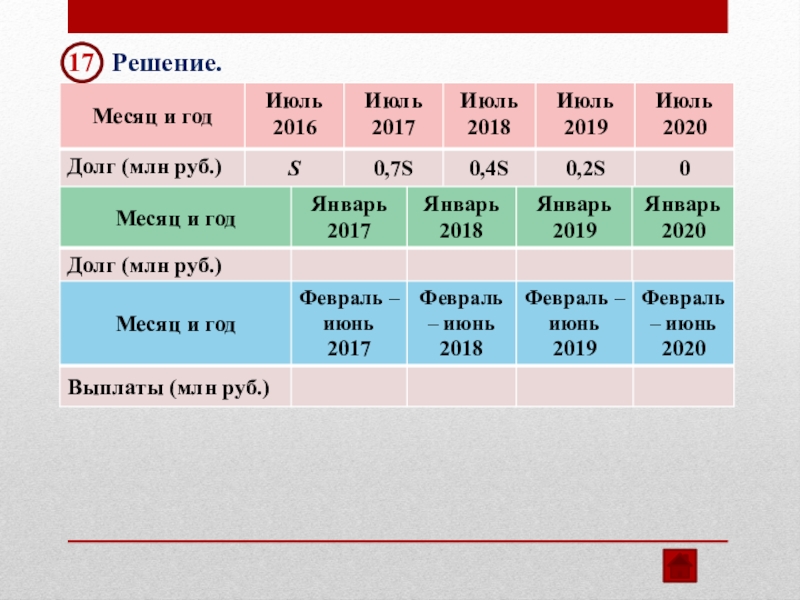
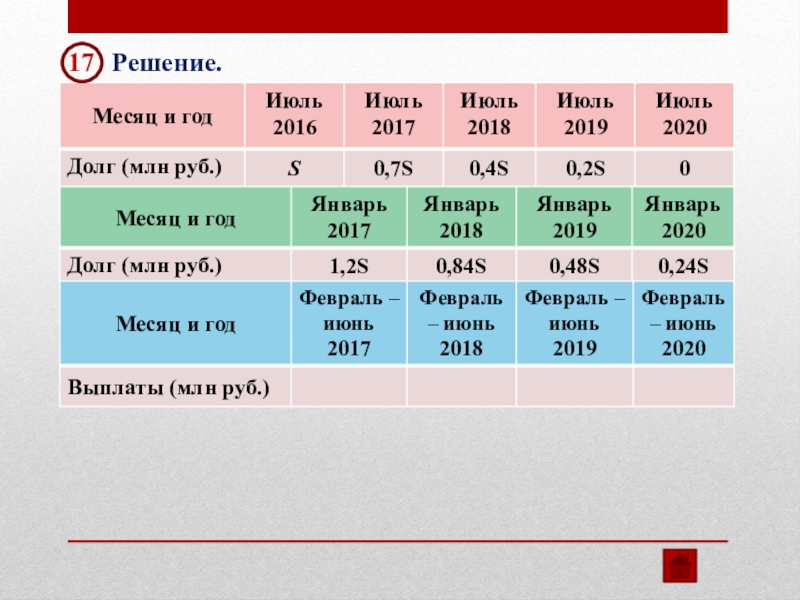
- 33. 17 Решение.
- 34. 17 Решение.
- 35. 17 Решение.
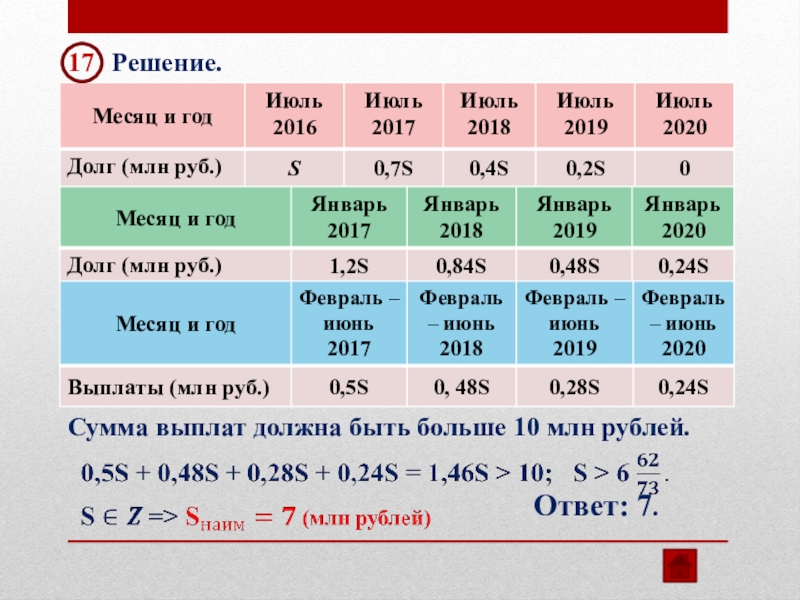
- 36. 17 Решение. Сумма выплат должна быть больше 10 млн рублей.Ответ: 7.
- 37. 17
- 38. 17 Решение.
- 39. 17 Решение.
- 40. 17 Решение.
- 41. 17 Решение.
- 42. 17 Решение.
- 43. 17 Решение.
- 44. 17 Решение.
- 45. 17 Решение.
- 46. 17
- 47. Типичные ошибки учащихся, допущенные в заданиях 17:при
- 48. 18 Решение. Преобразуем исходное уравнение:
- 49. 18
- 50. 18 Имеем:
- 51. 18 Исходное уравнение имеет ровно один корень при
- 52. 18
- 53. 18
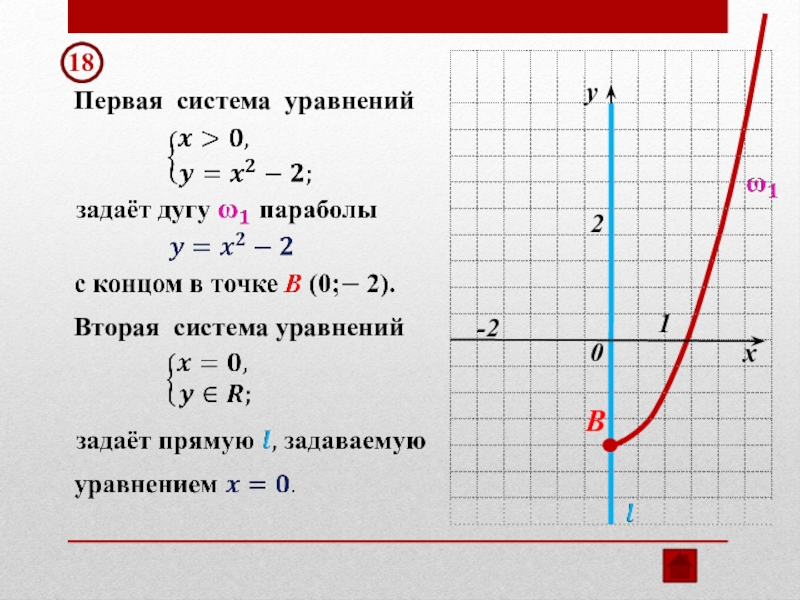
- 54. 18 Первая система уравненийВторая система уравнений y12-2B
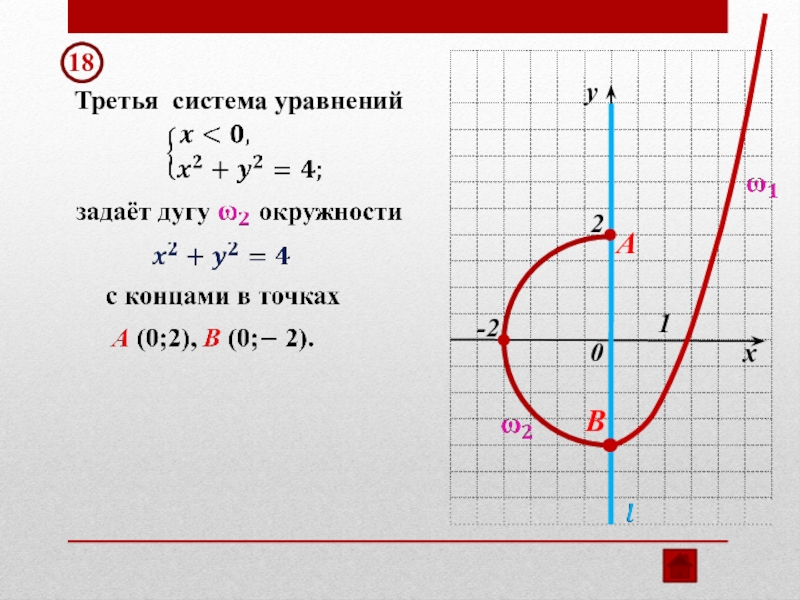
- 55. Третья система уравнений18 y12-2BA
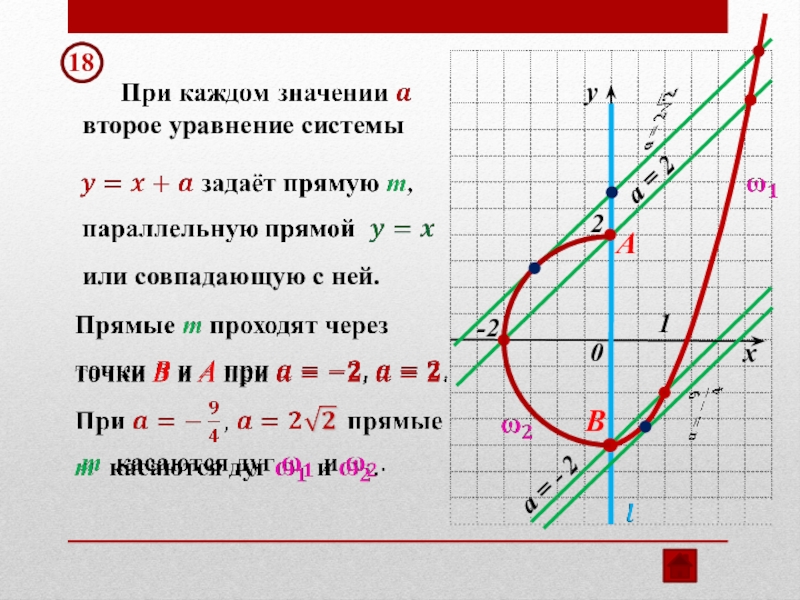
- 56. 18 y12-2BAвторое уравнение системыили совпадающую с ней.
- 57. y12-2BAa = 2a = - 218
- 58. 18 Исходная система имеет ровно три решения при
- 59. 18
- 60. Типичные ошибки учащихся, допущенные в заданиях 18:при
- 61. Слайд 61
- 62. Слайд 62
- 63. 19 Решение.b) Может ли в такой
- 64. Найдите наибольшее возможное значение среднего арифметического всех членов такой последовательности. 19 Решение.с)
- 65. 19 Последовательность 10, 12, 13, 15, 25,
- 66. 19
- 67. Типичные ошибки учащихся, допущенные в заданиях 19:отсутствие
- 68. 19
- 69. 19 Приведите пример такой последовательности, состоящей из четырёх членов, сумма которых равна 45.
- 70. b) Может ли в такая последовательность состоять
- 71. c) Какое наименьшее значение может принимать сумма
- 72. 19
- 73. 19
- 74. 19
- 75. Таким образом, последовательность с минимальной суммой чисел
- 76. Слайд 76
Слайд 8Типичные ошибки, допущенные учащимися в заданиях 13:
при применении формул приведения;
при решении
при нахождении корней данного уравнения, принадлежащих заданному отрезку;
потеря корней при решении уравнения разложением на множители;
вычислительные ошибки.
С этими заданиями в 2016 году справились
19,45% учащихся (2 балла),
5,94% учащихся (1 балл).
Слайд 16 С этими заданиями в 2016 году справились
1,03% учащихся (2
5.95% учащихся (1 балл).
Типичные ошибки, допущенные учащимися в заданиях 14:
при доказательстве параллельности плоскостей;
при проецировании точек на плоскость;
при решении простейшей планиметрической задачи;
при определении координат точек и векторов;
при вычислении искомых величин.
Слайд 21Типичные ошибки учащихся, допущенные в заданиях 15:
при выполнении преобразований неравенств;
при нахождении
при решении показательного неравенства;
вычислительные ошибки.
С этими заданиями в 2016 году справились
3,41% учащихся (2 балла),
2.09% учащихся (1 балл).
Слайд 31Типичные ошибки учащихся, допущенные в заданиях 16:
при доказательстве параллельности прямых;
при
вычислительные ошибки.
С этими заданиями в 2016 году справились
0,2% учащихся (3 балла),
0,32% учащихся (2 балла),
1,39% учащихся (1 балл).
Слайд 32
17
Найдите наименьшее значение S, при
Сумма выплат будет больше 10 млн рублей.
Слайд 45
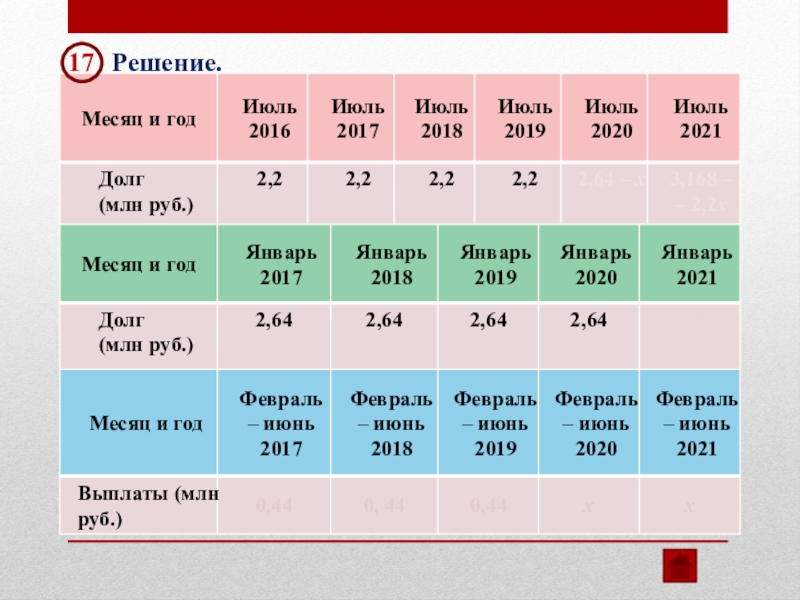
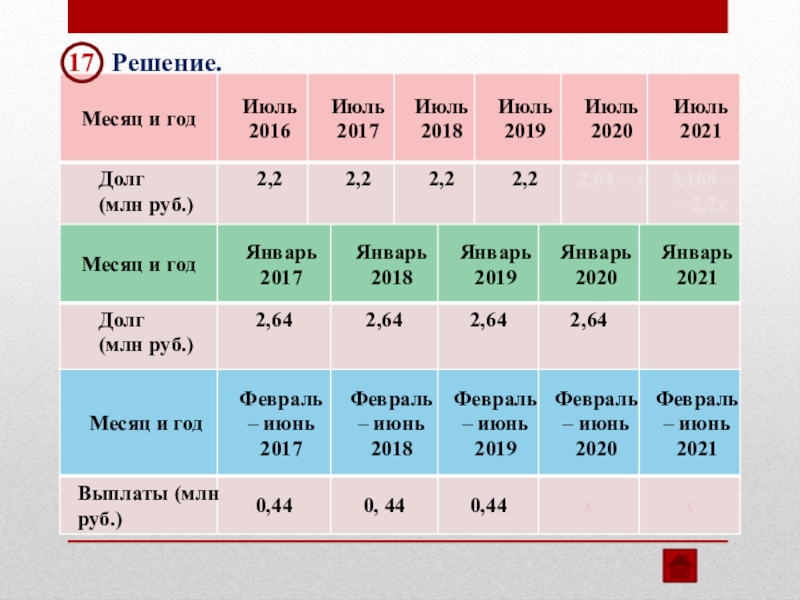
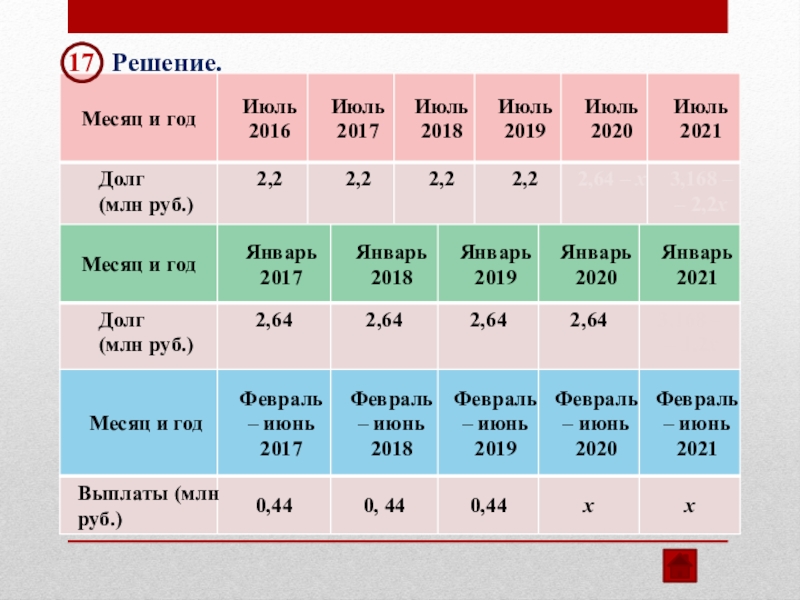
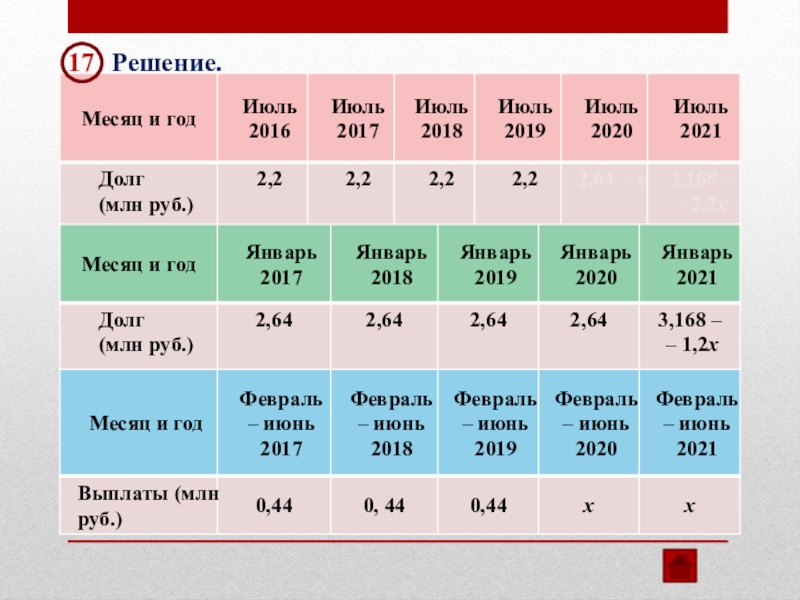
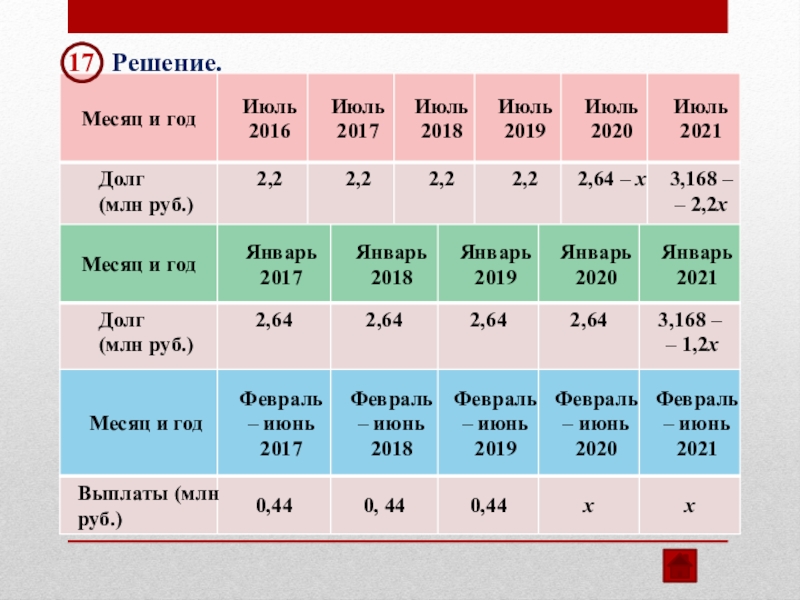
17
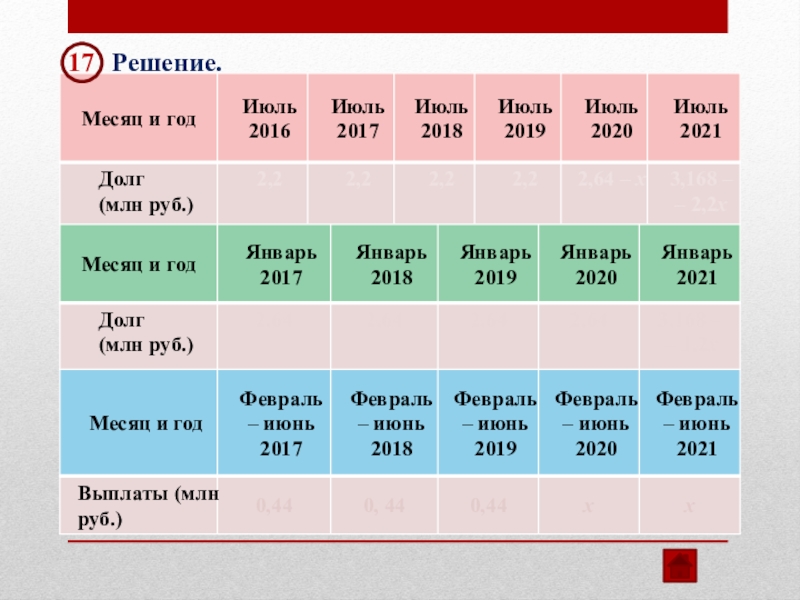
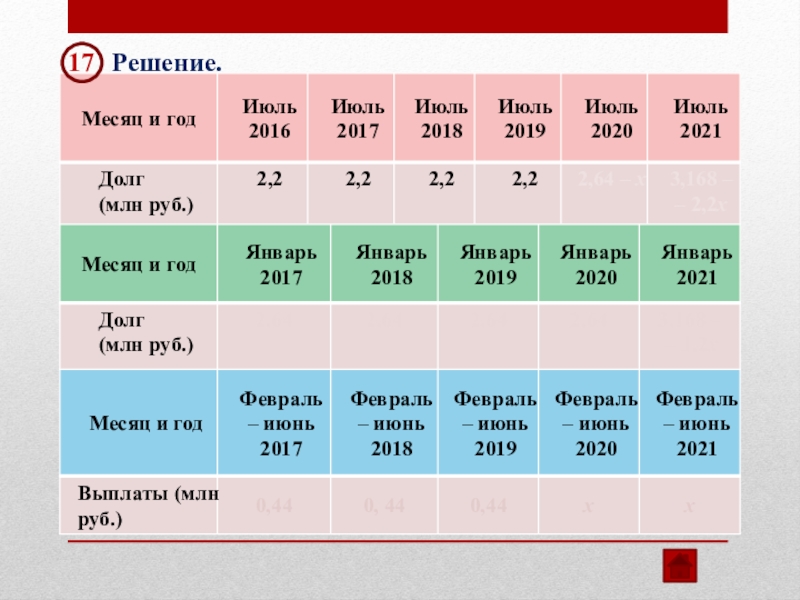
Решение.
В июле 2021 долг
Ответ: 1 млн рублей.
3,168 – 2,2х = 0
х = 1,44
Первая выплата составляет 0,44 млн рублей,
а последняя выплата 1,44 млн рублей.
Последняя выплата больше первой на 1 млн рублей.
Слайд 47Типичные ошибки учащихся, допущенные в заданиях 17:
при построении математической модели;
при
вычислительные ошибки.
С этими заданиями в 2016 году справились
6,0% учащихся (3 балла),
3,57% учащихся (2 балла),
1,6% учащихся (1 балл).
Слайд 60Типичные ошибки учащихся, допущенные в заданиях 18:
при составлении условий на параметр
были приобретены посторонние значения,
либо часть верных значений была потеряна;
при исследовании квадратных уравнений;
вычислительные ошибки
С этими заданиями в 2016 году справились
0,21% учащихся (4 балла),
0,08% учащихся (3 балла),
0,41% учащихся (2 балла),
7,16% учащихся (1 балл).
Слайд 61 Про
Приведите пример такой последовательности, для которой среднее арифметическое четырёх первых членов равно 11.
Может ли в такой последовательности среднее арифметическое четырёх первых членов быть равно 14?
Найдите наибольшее возможное значение среднего арифметического всех членов такой последовательности.
19
Слайд 62
Приведите
19
Слайд 6319
Решение.
b) Может ли в такой последовательности среднее
Значит, среднее арифметическое четырёх первых членов такой последовательности не может быть равно 14.
Слайд 64Найдите наибольшее возможное значение среднего арифметического всех членов такой последовательности.
19
Решение.
с)
Слайд 6519
Последовательность 10, 12, 13, 15, 25, 35, 45, 55, 65,
удовлетворяет условию задачи, а среднее арифметическое всех десяти её членов равно 35.
Ответ: а) 1, 10, 12, 21, 31, 35, 45, 55, 65, 69; b) нет; с) 35.
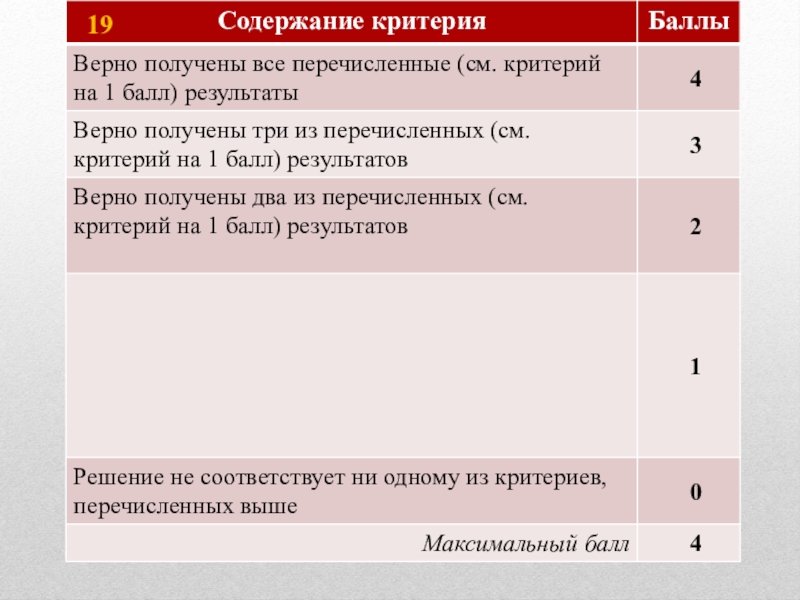
Слайд 67Типичные ошибки учащихся, допущенные в заданиях 19:
отсутствие обоснованного решения в пункте
доказательство того факта, что в наборе нет чисел, меньших 17, в п. в;
вычислительные ошибки.
С этими заданиями в 2016 году справились
0,32% учащихся (4 балла),
0,32% учащихся (3 балла),
3,49% учащихся (2 балла),
4,79% учащихся (1 балл).
Слайд 6919
Приведите пример такой последовательности, состоящей из четырёх членов, сумма которых
Слайд 70b) Может ли в такая последовательность состоять
из шести членов и
Например, последовательность
31, 10, 1, 1, 10, 31
удовлетворяет условию задачи.
19
Решение.
Слайд 71c) Какое наименьшее значение может принимать сумма членов такой последовательности при
19
Решение.
То есть последовательность разностей соседних
членов последовательности возрастает.
Слайд 75Таким образом, последовательность с минимальной суммой чисел содержится в последовательности
…;
1; 2; 4; 7; 11; 16; 22; 29; 37; 46; 56; …
Наименьшей суммой , равной 50, обладает последовательность, состоящая из 10 наименьших чисел этой последовательности:
11; 7; 4; 2; 1; 1; 2; 4; 7; 11.
19
Ответ: а) 1, 3, 10, 31; b) да; с) 50.