- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задание №5 ГИА Графики функций
Содержание
- 1. Презентация по математике на тему Задание №5 ГИА Графики функций
- 2. Линейная функция Общий вид у=кх+в, графиком является
- 3. Функция обратной пропорциональности Графиком функции вида
- 4. Квадратичная функцияОбщий вид Графиком является парабола. Направление
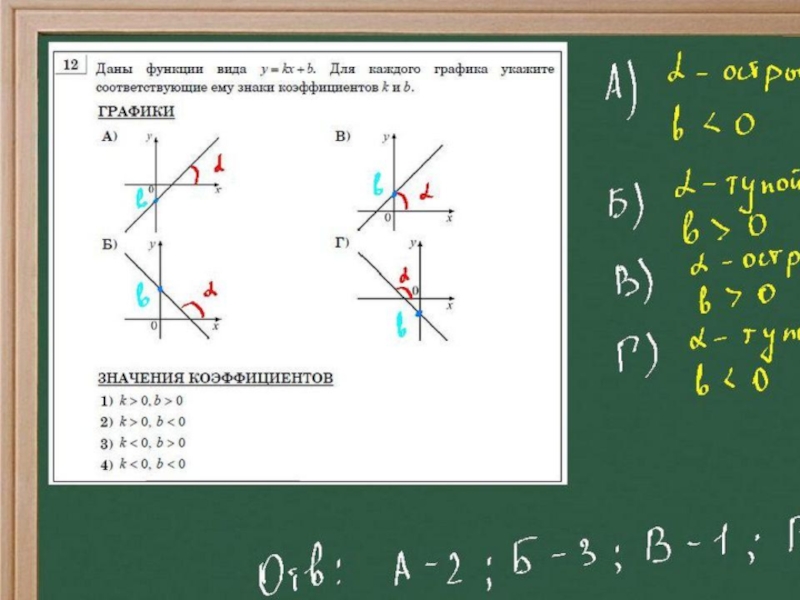
- 5. Даны функции вида у=кх+в. Для каждого графика укажите соотвеиствующие ему знаки коэффициентов к и в
- 6. Слайд 6
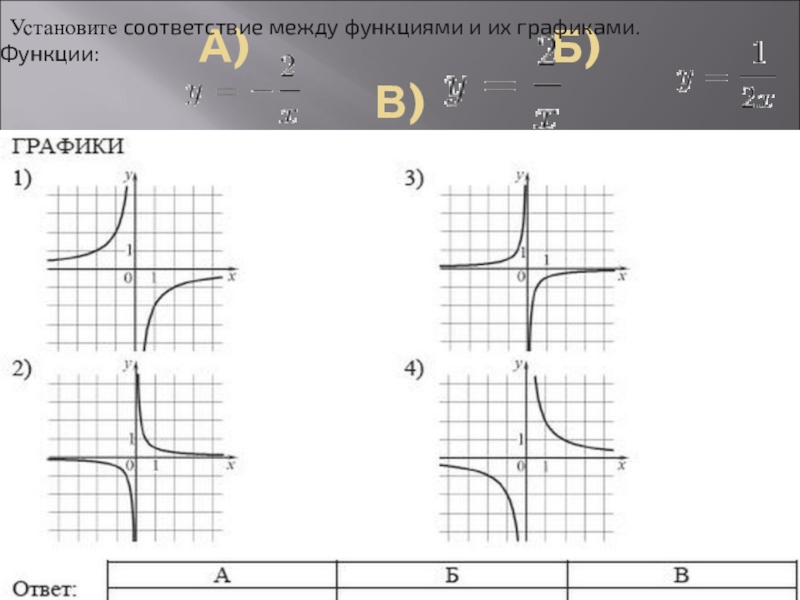
- 7. А)
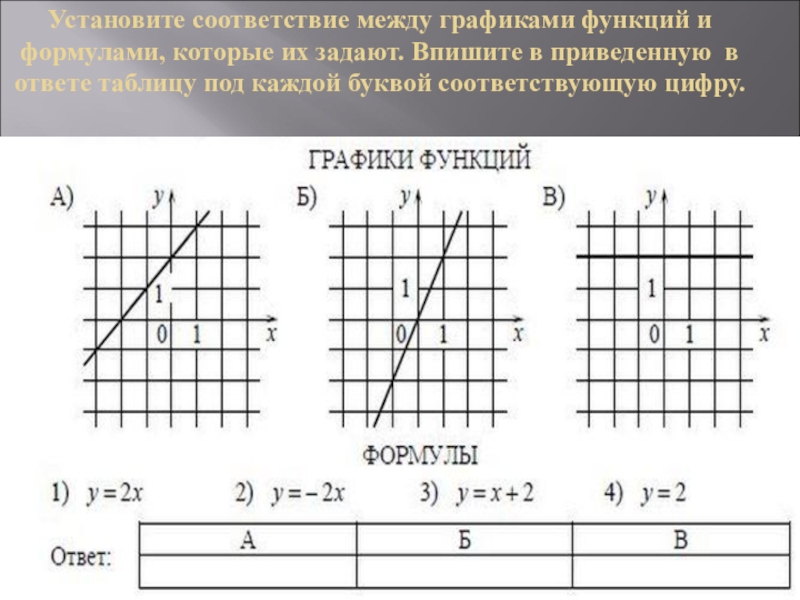
- 8. Установите соответствие между графиками функций и формулами,
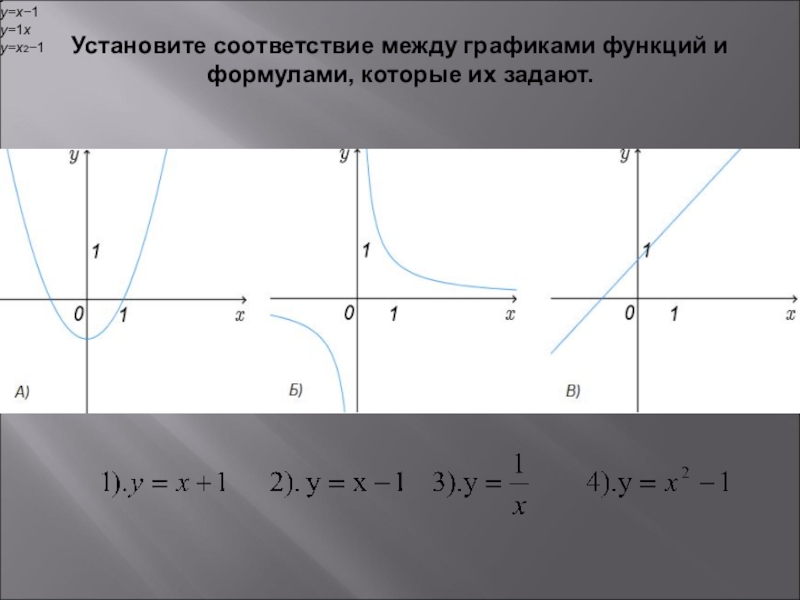
- 9. Установите соответствие между графиками функций и формулами, которые их задают. y=x+1y=x−1y=1xy=x2−1
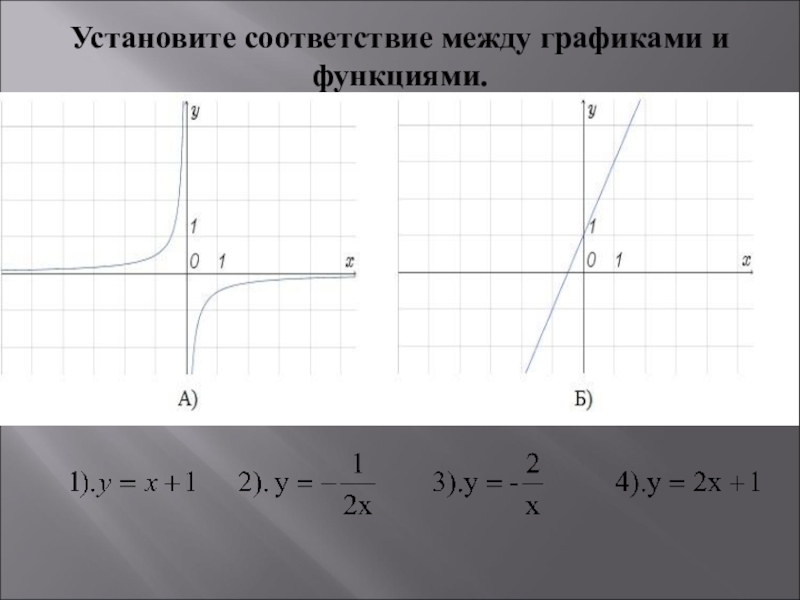
- 10. Установите соответствие между графиками и функциями.
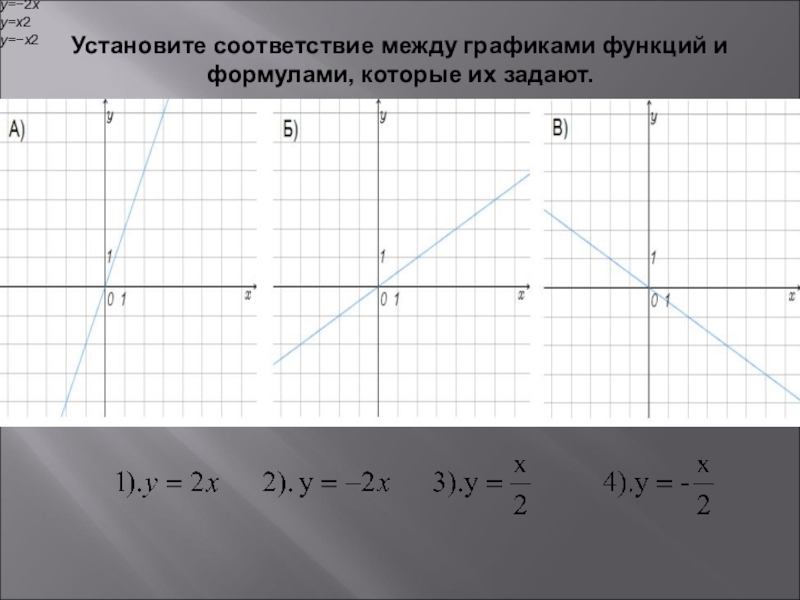
- 11. Установите соответствие между графиками функций и формулами, которые их задают. y=2xy=−2xy=x2y=−x2
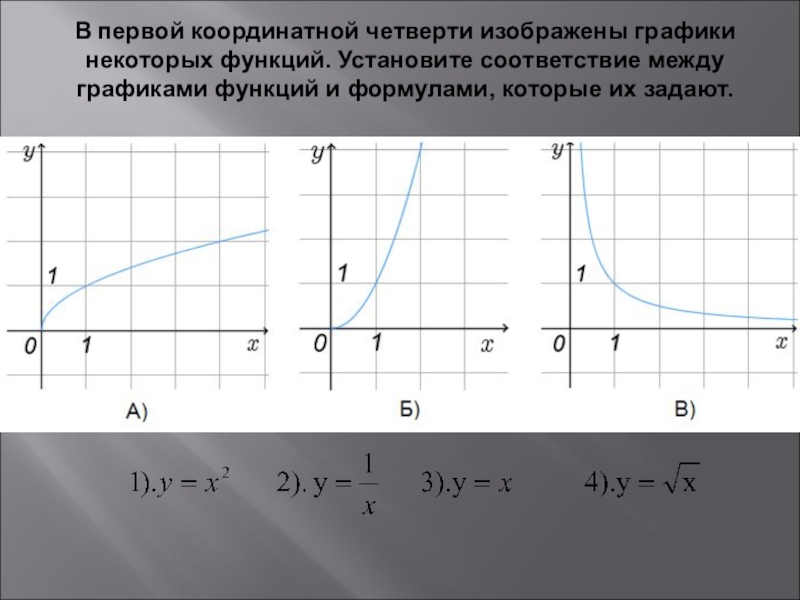
- 12. В первой координатной четверти изображены графики некоторых
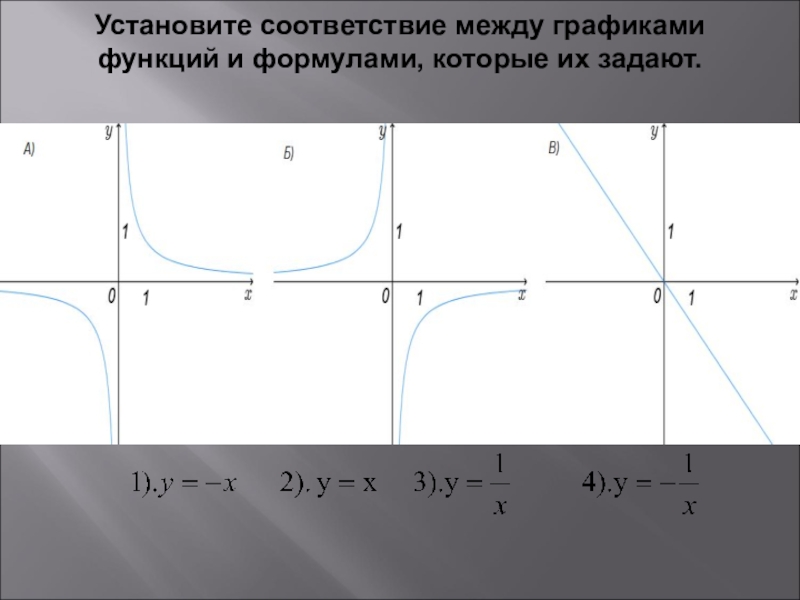
- 13. Установите соответствие между графиками функций и формулами, которые их задают.
- 14. «Число, положение
- 15. Слайд 15
- 16. Комбинаторика – самостоятельнаяветвь математической науки
- 17. КОМБИНАТОРИКА - это раздел математики, в
- 18. Разделы
- 19. «Вперед поедешь –
- 20. Слайд 20
- 21. n-факториал- это произведение всех натуральных чисел
- 22. ЗадачаКвартетПроказница МартышкаОсёл,Козёл,Да косолапый МишкаЗатеяли играть квартет…Стой, братцы
- 23. Решение:Здесь n=4, поэтому способов «усесться чинно в
- 24. Размещения – соединения,
- 25. Задача В группе ТД – 21
- 26. Решение задачи: Ответ:
- 27. Сочетания– соединения, содержащие по m предметов
- 28. Задача Студентам дали список из 10 учебников,
- 29. Решение задачи: Ответ: число
- 30. Библиографическая
- 31. Особая примета
- 32. Слайд 32
- 33. Исторические сведения Комбинаторика как наука стала развиваться
- 34. Исторические сведенияДата рождения: 1 июля 1646 г.
- 35. Связь комбинаторики с другими областями математики:
- 36. Фигурные числа .
- 37. Фигурные числа В древности вычислители
- 38. Комбинаторика в различных областяхжизнедеятельности человека.ЛитератураБылиныСказки_Басни__
- 39. Электротехника В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
- 40. Государственная
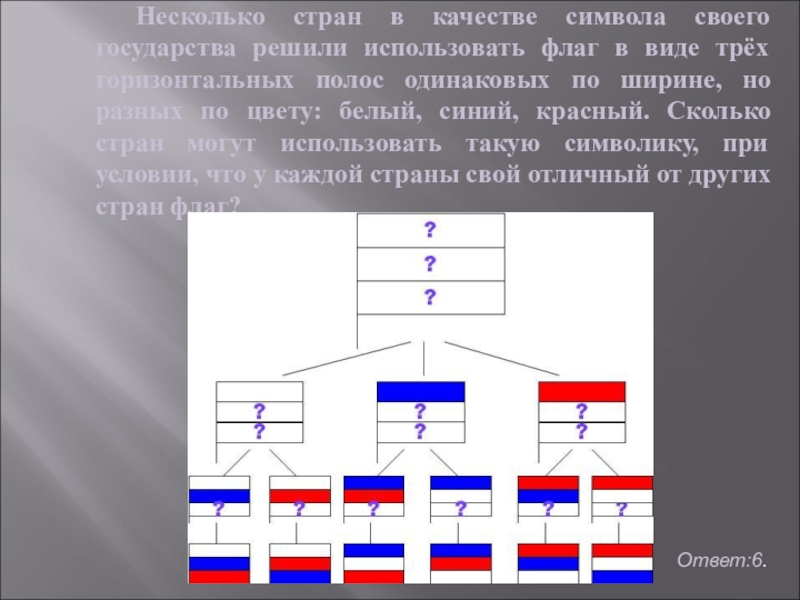
- 41. Несколько стран в качестве символа своего государства
- 42. Игра ШахматыВыдающиеся шахматисты Клод Шеннон и Михаил
- 43. Игра Кубик Рубика Необыкновенно популярной головоломкой
- 44. Меню на завтракНа завтрак Вова может выбрать:
- 45. ГИПОТЕЗАКомбинаторика интересна и имеет широкий спектр практической направленности.
- 46. ВЫВОД Комбинаторика имеет огромное значение в различных
- 47. ВЫВОДУсиление интереса к комбинаторике в последнее время
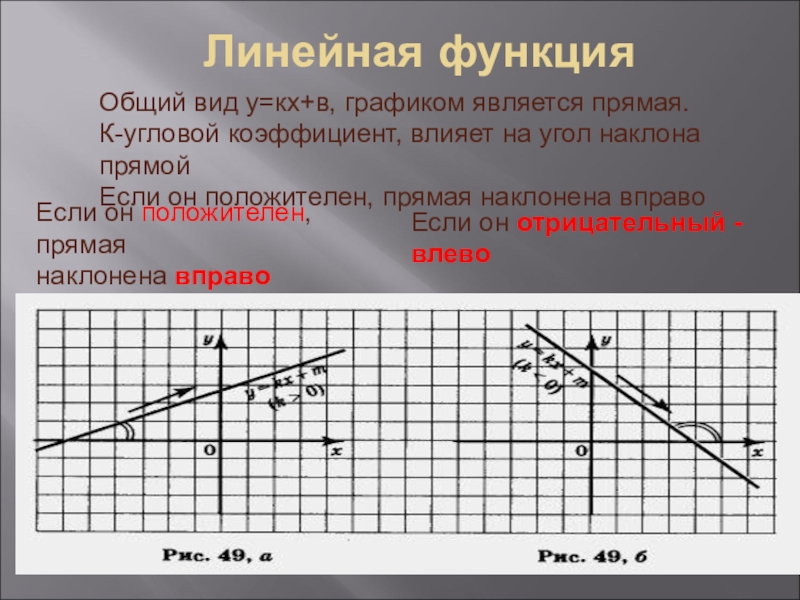
Слайд 2Линейная функция
Общий вид у=кх+в, графиком является прямая.
К-угловой коэффициент, влияет на
Если он положителен, прямая наклонена вправо
Если он отрицательный -влево
Если он положителен, прямая
наклонена вправо
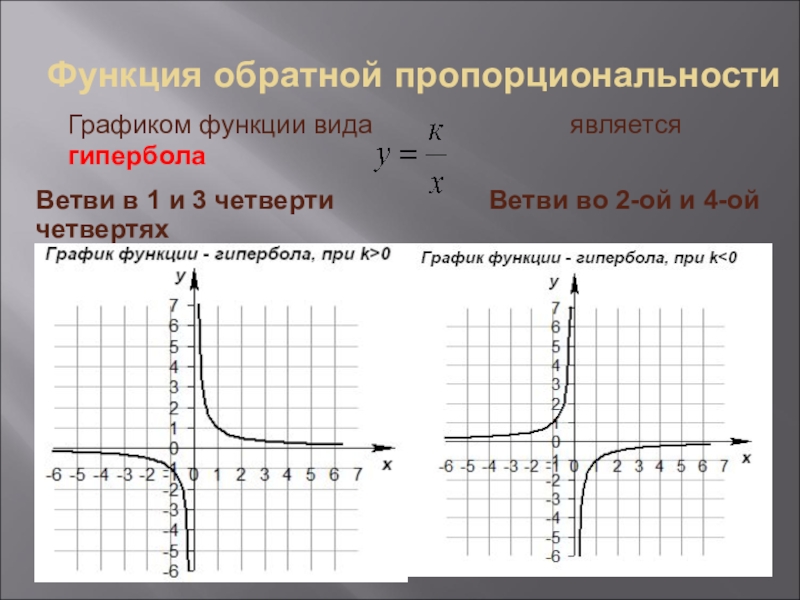
Слайд 3Функция обратной пропорциональности
Графиком функции вида
Ветви в 1 и 3 четверти Ветви во 2-ой и 4-ой четвертях
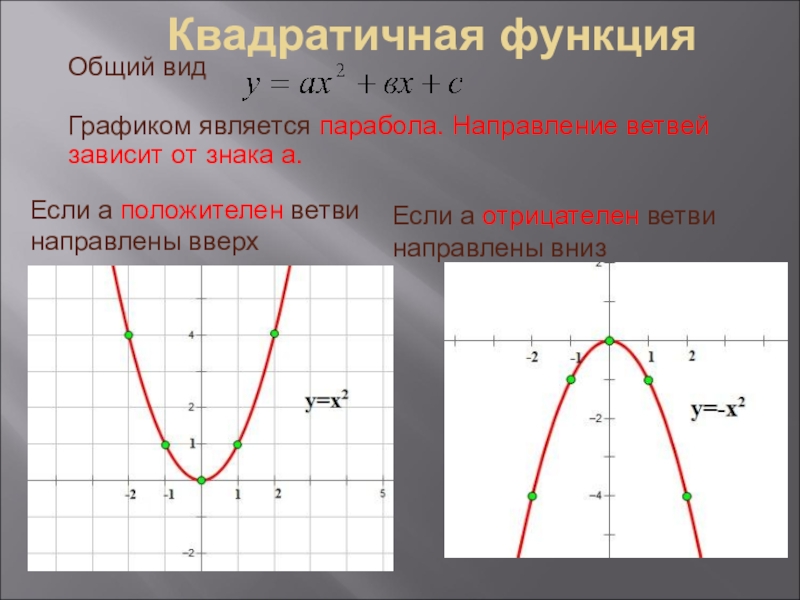
Слайд 4Квадратичная функция
Общий вид
Графиком является парабола. Направление ветвей зависит от знака
Если а положителен ветви направлены вверх
Если а отрицателен ветви направлены вниз
Слайд 5Даны функции вида у=кх+в. Для каждого графика укажите соотвеиствующие ему знаки
Слайд 8Установите соответствие между графиками функций и формулами, которые их задают. Впишите
Слайд 9Установите соответствие между графиками функций и формулами, которые их задают.
y=x+1
y=x−1
y=1x
y=x2−1
Слайд 11Установите соответствие между графиками функций и формулами, которые их задают.
y=2x
y=−2x
y=x2
y=−x2
Слайд 12В первой координатной четверти изображены графики некоторых функций. Установите соответствие между
Слайд 14 «Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к
Слайд 17КОМБИНАТОРИКА
- это раздел математики, в котором изучаются простейшие «соединения»:
(Большой Энциклопедический Словарь)
- происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Слайд 19 «Вперед поедешь – голову сложишь, направо
Слайд 20 Перестановки – соединения, которые
Слайд 21 n-факториал- это произведение всех натуральных чисел от до единицы до n, обозначают
Слайд 22Задача
Квартет
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка,
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Сколькими способами можно рассадить четырех музыкантов?
Слайд 23Решение:
Здесь n=4, поэтому способов «усесться чинно в ряд» имеется
P =
Слайд 24 Размещения – соединения, содержащие по m предметов из числа n данных,
Слайд 25Задача
В группе ТД – 21 обучается
24 студента.
Сколькими способами можно
Слайд 26 Решение задачи: Ответ: число способов равно числу размещений из 24 по 3,
Слайд 27 Сочетания– соединения, содержащие по m предметов из n, различающихся друг от
Слайд 28Задача
Студентам дали список из 10 учебников,
которые рекомендуется использовать для подготовки
Сколькими способами студент может выбрать из них 3 книги?
Слайд 30Библиографическая
Слайд 31 Особая примета комбинаторных задач -
Слайд 32 Решение
Слайд 33Исторические сведения
Комбинаторика как наука стала развиваться в XIII в. параллельно
Первые научные исследования по этой теме принадлежат итальянским ученым Дж. Кардано, Н. Чарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б.Пискамо (1623-1662) и П. Ферма.
Комбинаторику, как самостоятельный раздел математики, первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».
Слайд 34Исторические сведения
Дата рождения: 1 июля 1646 г.
Место рождения: Лейпциг, Германия
Дата
Место смерти: Ганновер, Германия
Школа/традиция: рационализм
Направление: Европейская философия
Основные интересы: Метафизика, эпистемология, наука, математика.
Лейбниц Готфрид Вильгельм
Слайд 35Связь комбинаторики с другими областями математики: Имеет широкий спектр применения в информатике и
алгебра,
геометрия,
теория вероятностей.
Слайд 36Фигурные числа
.
Солдаты стоят правильными рядами,
Слайд 37 Фигурные числа
В древности вычислители часто считали с помощью
Слайд 39Электротехника
В коридоре висят три
лампочки. Сколько имеется
различных способов освещения коридора?
Слайд 41 Несколько стран в качестве символа своего государства решили использовать флаг в
Ответ:6.
Слайд 42Игра Шахматы
Выдающиеся шахматисты Клод Шеннон и Михаил Ботвинник внесли огромный вклад
Компьютерные шахматы — едва ли не самый убедительный пример за полвека развития информационных технологий, когда именно в интеллектуальной деятельности автомат успешно соперничает с человеком.
Слайд 43Игра Кубик Рубика
Необыкновенно популярной головоломкой стал кубик Рубика, изобретенный
Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды.
Кубик Рубика служит не только развлечением, но и прекрасным наглядным пособием по комбинаторике.
Слайд 44Меню на завтрак
На завтрак Вова может выбрать: плюшку, бутерброд, пряник, или
Слайд 46ВЫВОД
Комбинаторика имеет огромное значение в различных областях науки и производственной
С комбинаторными величинами приходится иметь дело представителям многих специальностей: ученому – химику, биологу, конструктору, диспетчеру и т.п.
Комбинаторика используется в литературе, математике, музыке, в различных играх (нарды, шашки, шахматы). В каждой из этих игр приходится рассматривать различные сочетания фигур, и выигрывает тот, кто их лучше изучает, знает выигрышные комбинации и умеет избегать проигрышных.
Слайд 47ВЫВОД
Усиление интереса к комбинаторике в последнее время обуславливается бурным развитием кибернетики
Комбинаторика помогает развивать математические способности, сообразительность, логическое мышление, укрепляют память.
Таким образом, мы не только подтвердили гипотезу, что комбинаторика – это раздел математики, имеющий широкий спектр практической направленности, но и расширили диапазон своих знаний.