(навстречу и вдогонку)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи на движение по прямой
Содержание
- 1. Презентация по математике на тему Задачи на движение по прямой
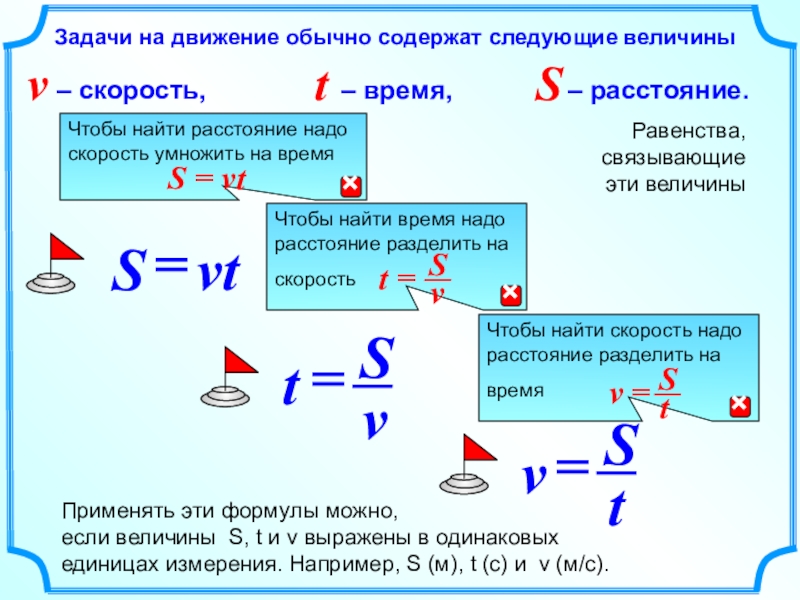
- 2. Задачи на движение обычно содержат следующие величиныРавенства,
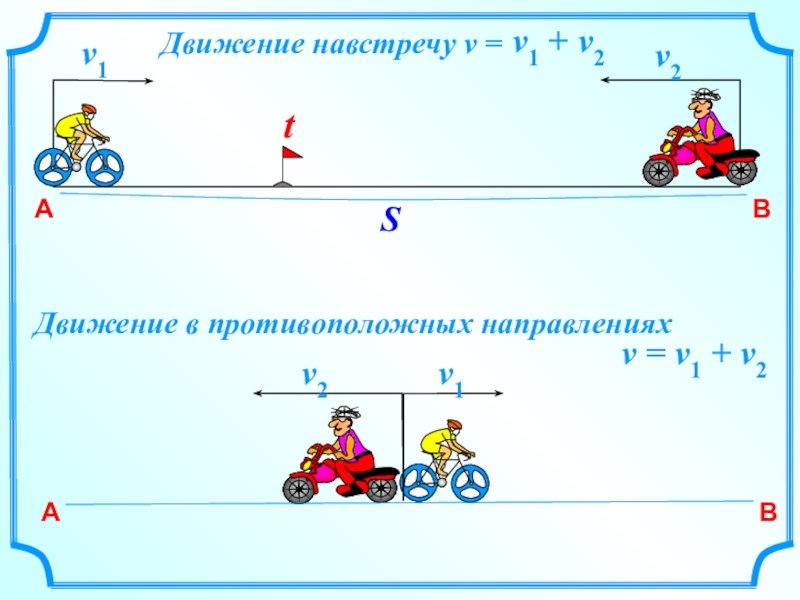
- 3. АBSv1v2Движение навстречу v = v1 + v2v = v1 + v2
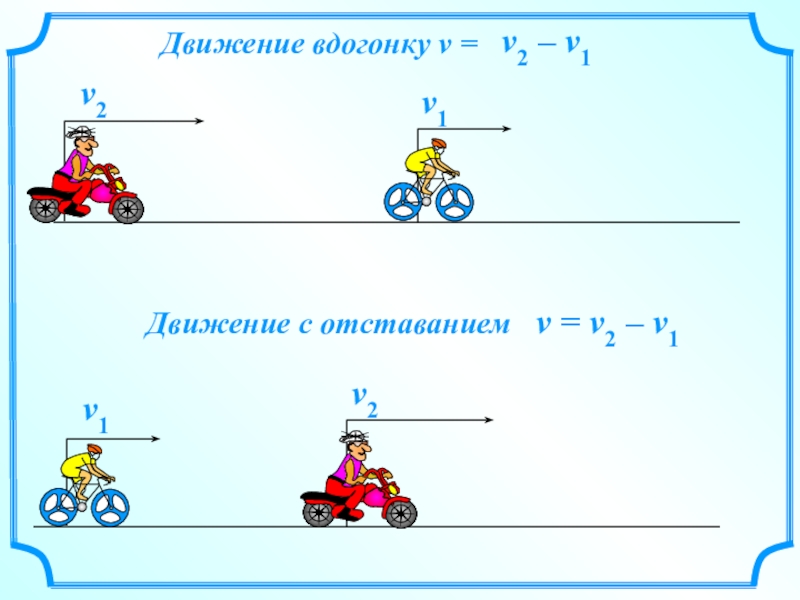
- 4. v1v2Движение вдогонку v = v2 – v1v = v2 – v1
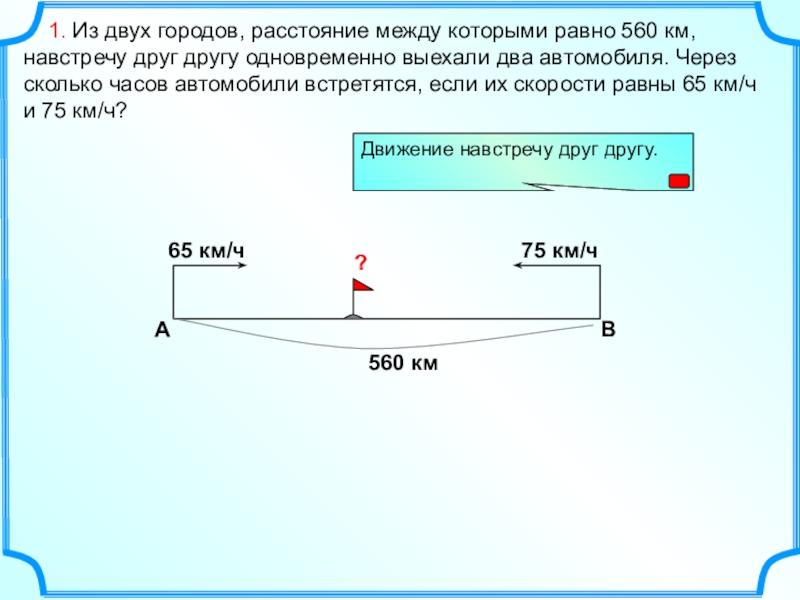
- 5. 1. Из двух городов, расстояние
- 6. Слайд 6
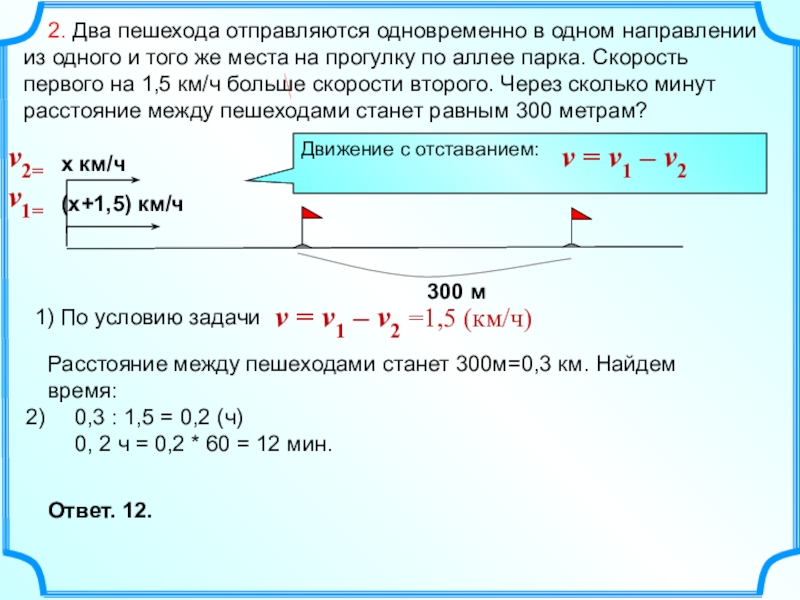
- 7. 2. Два пешехода отправляются одновременно
- 8. Слайд 8
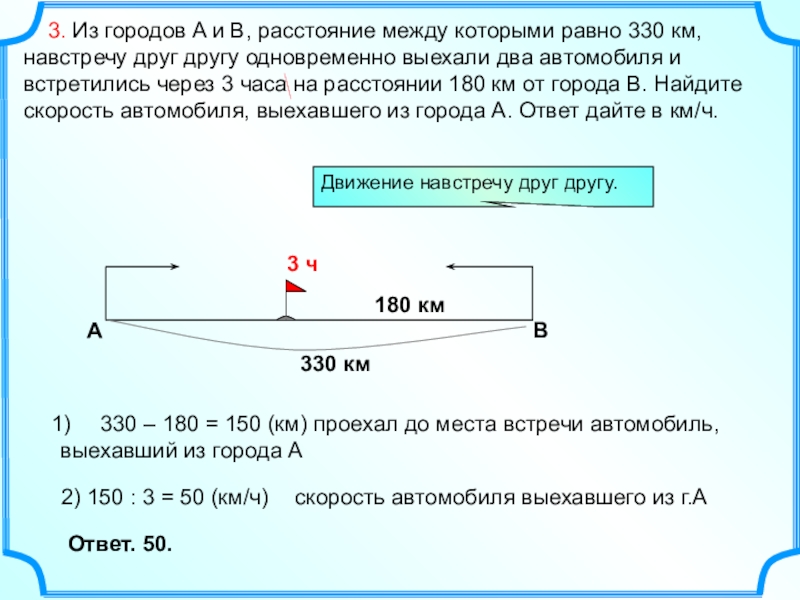
- 9. 3. Из городов A и
- 10. Слайд 10
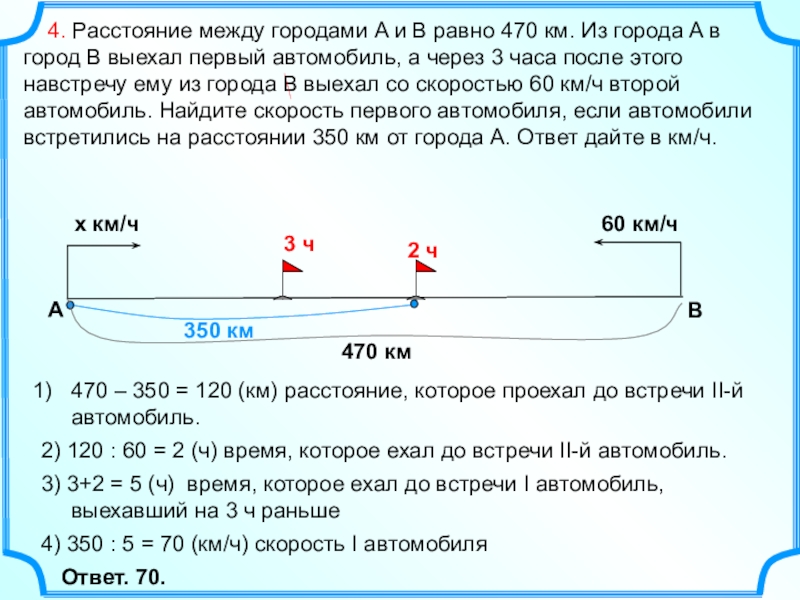
- 11. 470 – 350 = 120 (км) расстояние,
- 12. Слайд 12
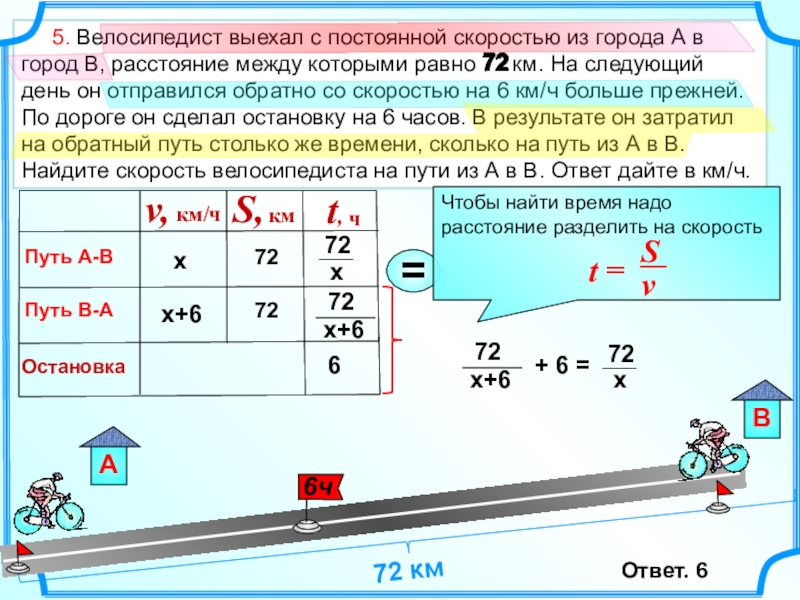
- 13. 5. Велосипедист выехал с
- 14. Ответ. 6
- 15. 6. Два велосипедиста одновременно отправились
- 16. Ответ. 8
- 17. Средняя скорость
- 18. Задача №1 Первую половину времени, затраченного на все
- 19. Решение.Ответ. 5.Пусть на весь путь турист затратил t часов.
- 20. Задача №2 Путешественник переплыл море на корабле со
- 21. Решение. Обозначим буквой S
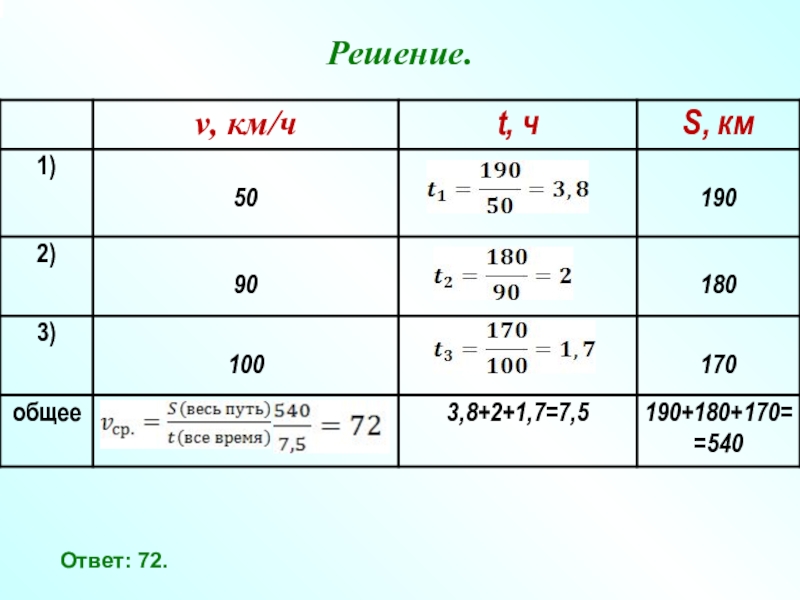
- 22. Задача №3 Первые 190 км грузовик ехал со скоростью
- 23. Решение. Ответ: 72.
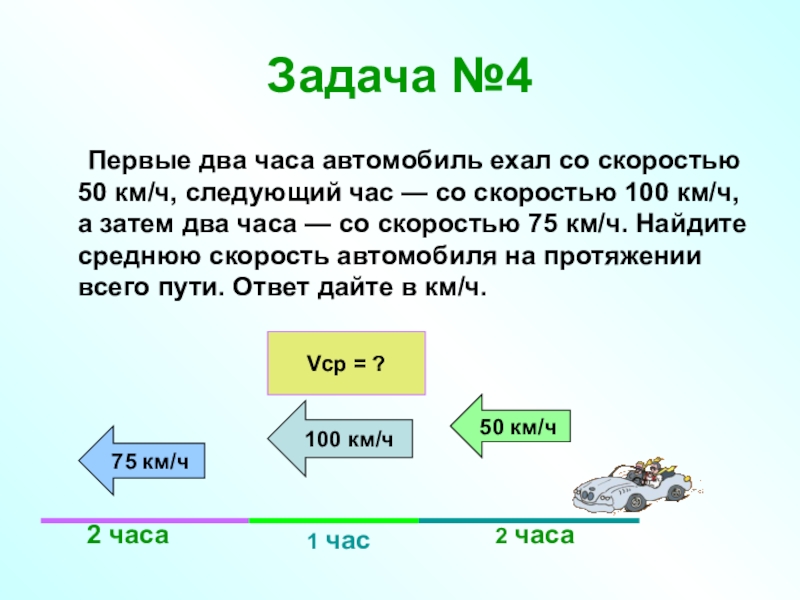
- 24. Задача №4 Первые два часа автомобиль ехал со
- 25. Решение: Составим выражение. В числителе определим весь путь, в знаменателе все время. Ответ: 70
- 26. Задача №5 Первую треть трассы автомобиль ехал со
- 27. Решение. Обозначим буквой S треть трассы. Ответ: 85,7
Задачи на движение обычно содержат следующие величиныРавенства, связывающие эти величиныПрименять эти формулы можно, если величины S, t и v выражены в одинаковых единицах измерения. Например, S (м), t (с) и v (м/с).
Слайд 2Задачи на движение обычно содержат следующие величины
Равенства, связывающие
эти величины
Применять эти
формулы можно,
если величины S, t и v выражены в одинаковых
единицах измерения. Например, S (м), t (с) и v (м/с).
если величины S, t и v выражены в одинаковых
единицах измерения. Например, S (м), t (с) и v (м/с).
Слайд 5 1. Из двух городов, расстояние между которыми равно 560
км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
А
B
65 км/ч
75 км/ч
Слайд 7 2. Два пешехода отправляются одновременно в одном направлении из
одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
1) По условию задачи
Расстояние между пешеходами станет 300м=0,3 км. Найдем время:
0,3 : 1,5 = 0,2 (ч)
0, 2 ч = 0,2 * 60 = 12 мин.
Ответ. 12.
v = v1 – v2
v1=
v2=
v = v1 – v2 =1,5 (км/ч)
Слайд 9 3. Из городов A и B, расстояние между которыми
равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
А
B
180 км
330 – 180 = 150 (км) проехал до места встречи автомобиль,
выехавший из города А
Движение навстречу друг другу.
Ответ. 50.
скорость автомобиля выехавшего из г.А
2) 150 : 3 = 50 (км/ч)
Слайд 11470 – 350 = 120 (км) расстояние, которое проехал до встречи
II-й автомобиль.
4. Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
А
B
2) 120 : 60 = 2 (ч) время, которое ехал до встречи II-й автомобиль.
3) 3+2 = 5 (ч) время, которое ехал до встречи I автомобиль, выехавший на 3 ч раньше
Ответ. 70.
2 ч
х км/ч
4) 350 : 5 = 70 (км/ч) скорость I автомобиля
Слайд 13 5. Велосипедист выехал с постоянной скоростью из города
А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Путь В-А
х
72
х+6
72
72 км
Ответ. 6
72
72
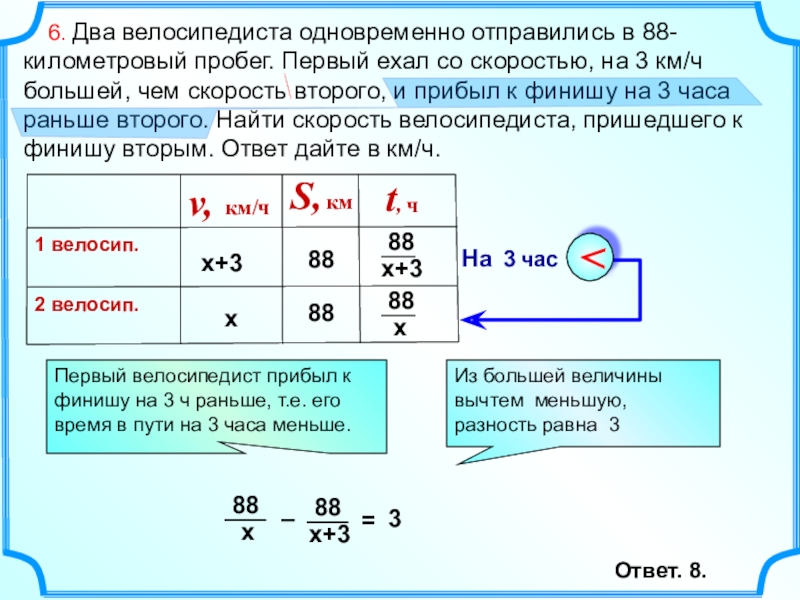
Слайд 15 6. Два велосипедиста одновременно отправились в 88-километровый пробег. Первый
ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
х
88
88
Первый велосипедист прибыл к финишу на 3 ч раньше, т.е. его время в пути на 3 часа меньше.
Ответ. 8.
Из большей величины вычтем меньшую,
разность равна 3
Слайд 18Задача №1
Первую половину времени, затраченного на все путешествие, турист двигался со
скоростью 4 км/ч, а вторую половину времени - со скоростью 6 км/ч. Какова средняя скорость движения туриста на протяжении всего путешествия?
4 км/ч
6 км/ч
Vср = ?
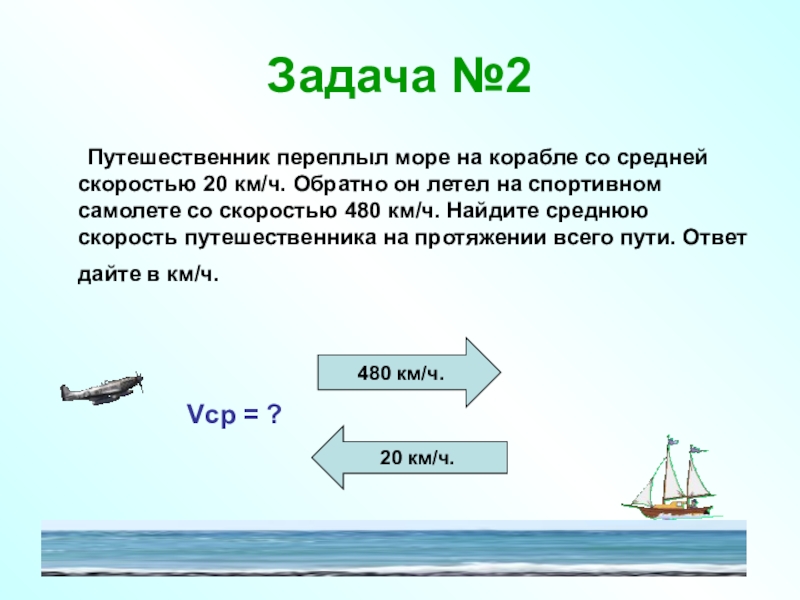
Слайд 20Задача №2
Путешественник переплыл море на корабле со средней скоростью 20 км/ч.
Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
20 км/ч.
480 км/ч.
Vср = ?
Слайд 21Решение.
Обозначим буквой S путь в один конец,
тогда весь путь туда и обратно будет 2S.
2S - это весь путь. Разделим весь путь на все время
2S - это весь путь. Разделим весь путь на все время
Ответ: 38,4
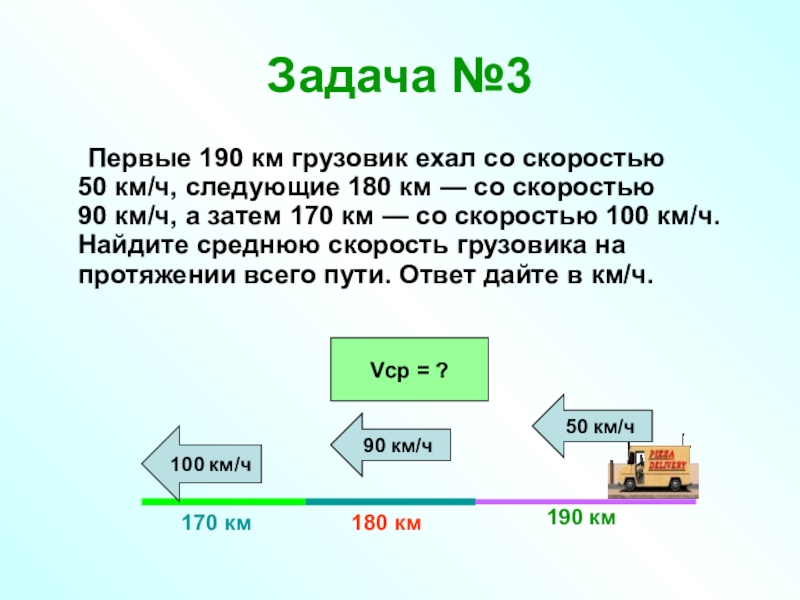
Слайд 22Задача №3
Первые 190 км грузовик ехал со скоростью 50 км/ч, следующие 180 км — со
скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость грузовика на протяжении всего пути. Ответ дайте в км/ч.
190 км
50 км/ч
180 км
90 км/ч
170 км
100 км/ч
Vср = ?
Слайд 24Задача №4
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий
час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2 часа
50 км/ч
1 час
100 км/ч
2 часа
75 км/ч
Vср = ?
Слайд 25Решение:
Составим выражение. В числителе определим весь путь, в знаменателе все время.
Ответ: 70
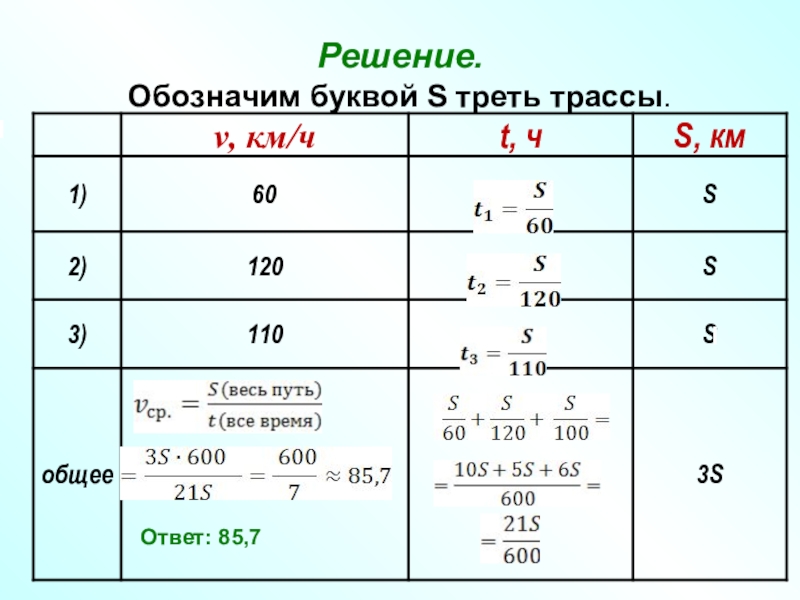
Слайд 26Задача №5
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую
треть — со скоростью 120 км/ч, а последнюю — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
60 км/ч
120 км/ч
110 км/ч
Vср = ?
