- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи на оптимизацию
Содержание
- 1. Презентация по математике на тему Задачи на оптимизацию
- 2. Легенда о финикийской царице ДидонеВ древности на
- 3. Легенда о финикийской царице ДидонеКорабли принцессы подплыли
- 4. Переформулируем задачу Дидоны: Огородить участок наибольшей площади
- 5. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 6. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 7. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 8. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 9. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 10. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 11. Задача:Периметр прямоугольника равен 40 см. Какую длину
- 12. Задачи для самостоятельного решения:1) Число 24 представьте
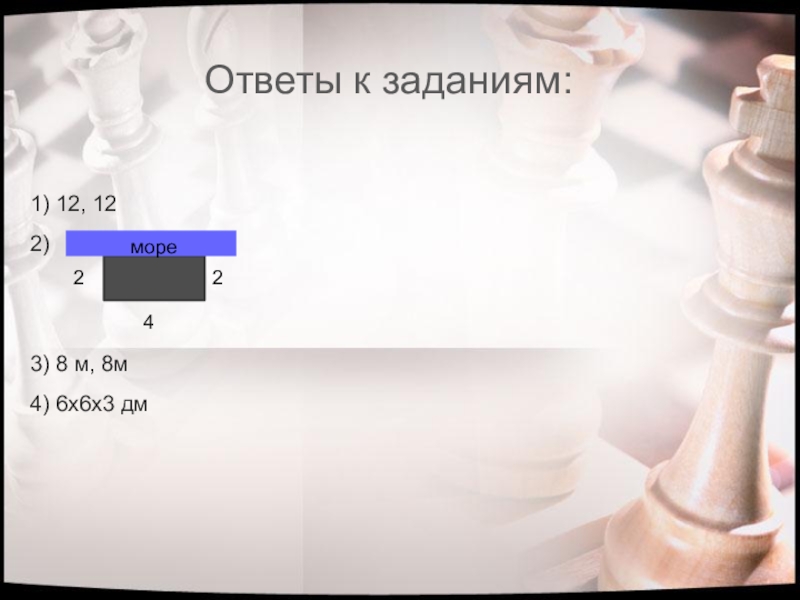
- 13. Ответы к заданиям:1) 12, 122) 3) 8 м, 8м4) 6х6х3 дмморе224
- 14. Использованные ресурсы:Мордкович А.Г. Алгебра и начала математического
Слайд 2Легенда о финикийской царице Дидоне
В древности на территории нынешнего Ливана был
Но по факту государством правил муж Дидоны Сихей. Повзрослевший Пигмалион приказал убить правителя, а его сестра Дидона, опасаясь участи мужа, бежала из Тира.
Слайд 3Легенда о финикийской царице Дидоне
Корабли принцессы подплыли к берегам Северной Африки,
Но Дидона его перехитрила! Она велела разрезать шкуру на шнуры, растянула их и огородила огромную территорию. Так был основан город Карфаген.
Слайд 4Переформулируем задачу Дидоны: Огородить участок наибольшей площади при фиксированной длине веревки
-
Задачи на оптимизацию
Слайд 5Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
15 см
5 см
5 см
15 см
S = 15·5 = 75 см2
Р = 40 см
10 см
10 см
10 см
10 см
S = 10·10 = 100 см2
Р = 40 см
Попробуем представить некоторые варианты решения
Какой из этих вариантов лучше?
Слайд 6Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
х см
у см
у см
х см
Р = 40 см
Решение:
Составим математическую модель задачи: введём две переменные,
если на них есть ограничения, то укажем их.
х > 0
у > 0
Слайд 7Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
х см
у см
у см
х см
Р = 40 см
Решение:
2. Воспользуемся известными данными и выразим одну переменную через другую
х > 0
у > 0
Р = х + у + х + у = 2х + 2у = 40
2х + 2у = 40
х + у = 20
у = 20 - х
Слайд 8Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
х см
у см
у см
х см
Р = 40 см
Решение:
3. Составим функцию для исследования (по условию задачи она должна принимать наименьшее или наибольшее значение)
х > 0
у > 0
S = х·у
у = 20 - х
S = х·(20 – x)
S = 20x – x2
Слайд 9Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
х см
у см
у см
х см
Р = 40 см
Решение:
4. Исследуем функцию на экстремум.
х > 0
у > 0
у = 20 - х
S = 20x – x2
S΄ = 20 – 2x
S΄ = 0
20 – 2x = 0
– 2x = -20
x = 10
0
10
S΄
x
+
-
т. max
x = 10
Слайд 10Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
х см
у см
у см
х см
Р = 40 см
Решение:
5. Вычислим значение введённых переменных.
х > 0
у > 0
у = 20 - х
x = 10
у = 20 - 10
у = 10
Слайд 11Задача:
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
10 см
10 см
10 см
10 см
Р = 40 см
Ответ:
стороны прямоугольника должны быть 10 см и 10 см, чтобы при периметре 40 см площадь прямоугольника была наибольшей
Слайд 12Задачи для самостоятельного решения:
1) Число 24 представьте в виде суммы двух
2) Дидона разрезала воловью шкуру. У неё получилась верёвка длиной 8 км. Она решила огородить участок суши прямоугольной формы, прилегающий к морю. Найдите, при каких размерах участок будет иметь наибольшую площадь.
3) Площадь прямоугольного земельного участка 64 м2. Какие должны быть длины сторон, чтобы оградить участок наименьшим количеством материала?
4) Стальной бак без верхней крышки должен иметь форму прямоугольного параллелепипеда с квадратным основанием и объемом 108 дм3. При каких размерах бака на его изготовление пойдет наименьшее количество стали?
Слайд 14Использованные ресурсы:
Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. Базовый
https://yandex.ru/images/search?text=легенда%20о%20Дидоне%20и%20Карфагене&img_url=https%3A%2F%2Fcs4.pikabu.ru%2Fpost_img%2F2016%2F06%2F29%2F9%2F1467215075116533880.jpg&pos=7&rpt=simage
https://happytravel.ru/blog/istoriya-i-legendy-karfagena/