- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи ЕГЭ: производная
Содержание
- 1. Презентация по математике на тему Задачи ЕГЭ: производная
- 2. Геометрический смысл производнойПроизводная в точке x 0
- 3. №1723 стр. 261№1728
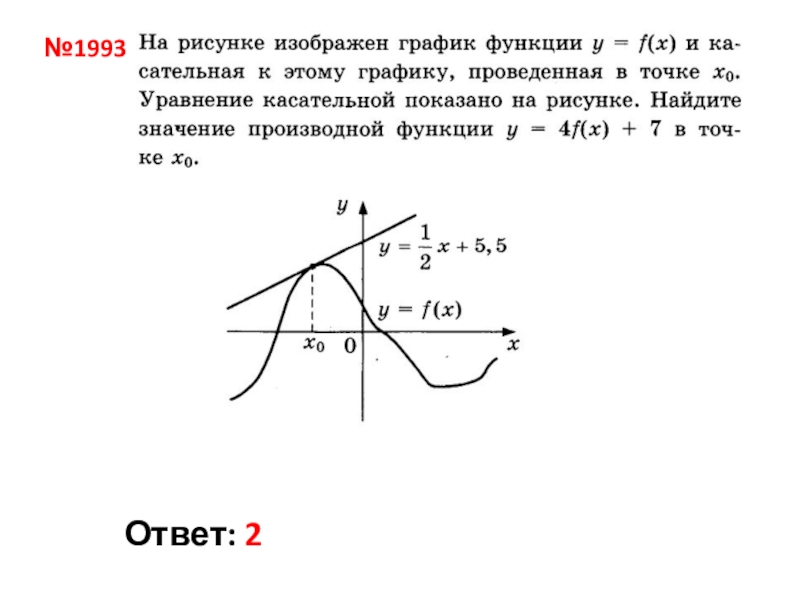
- 4. №1993Ответ: 2
- 5. №1729Т. к. касательная к графику функции параллельна
- 6. Ответ: 4
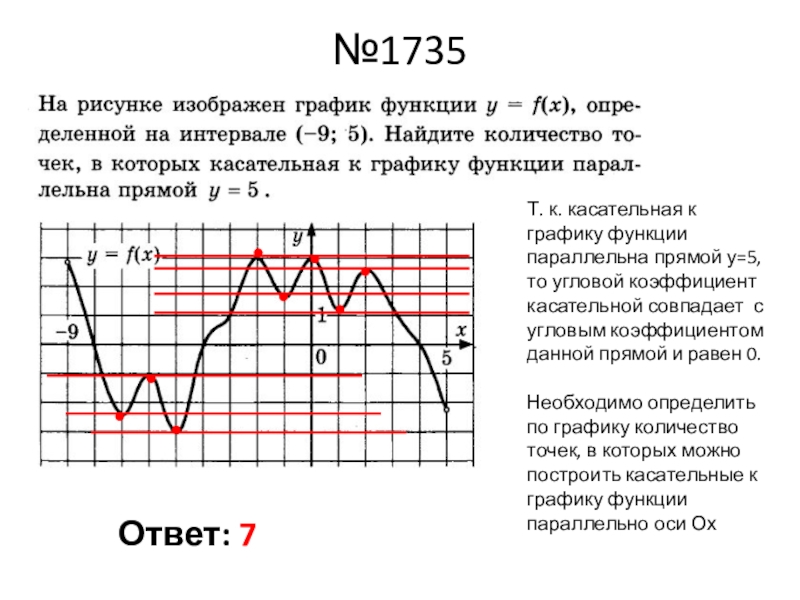
- 7. №1735Т. к. касательная к графику функции параллельна
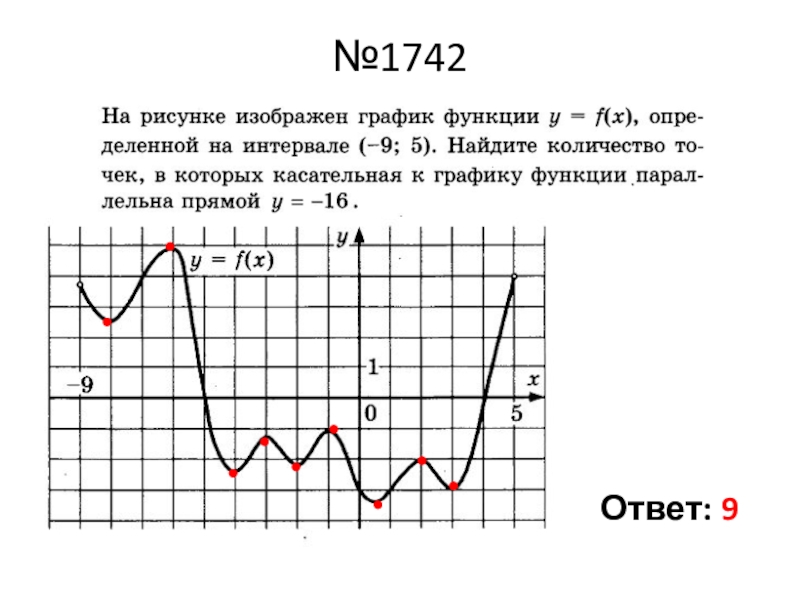
- 8. №1742Ответ: 9
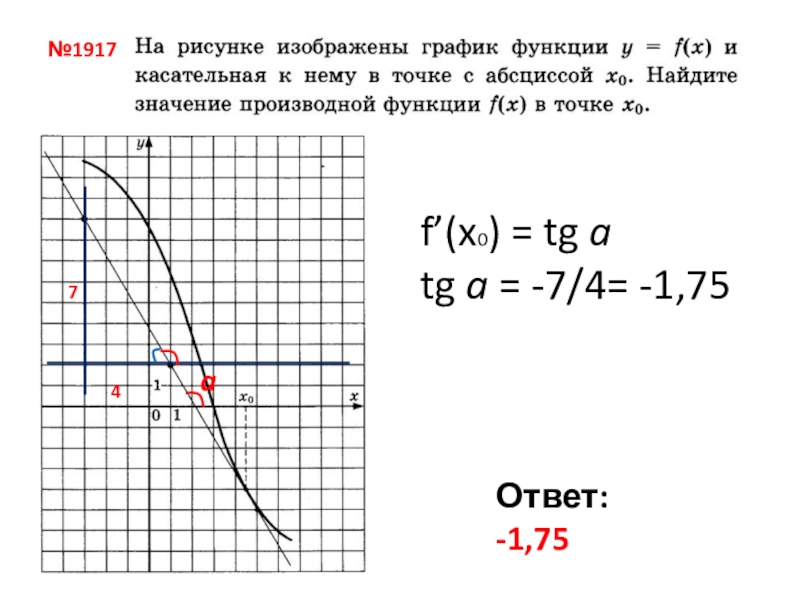
- 9. №1917f’(x0) = tg atg a = -7/4= -1,7574aОтвет: -1,75
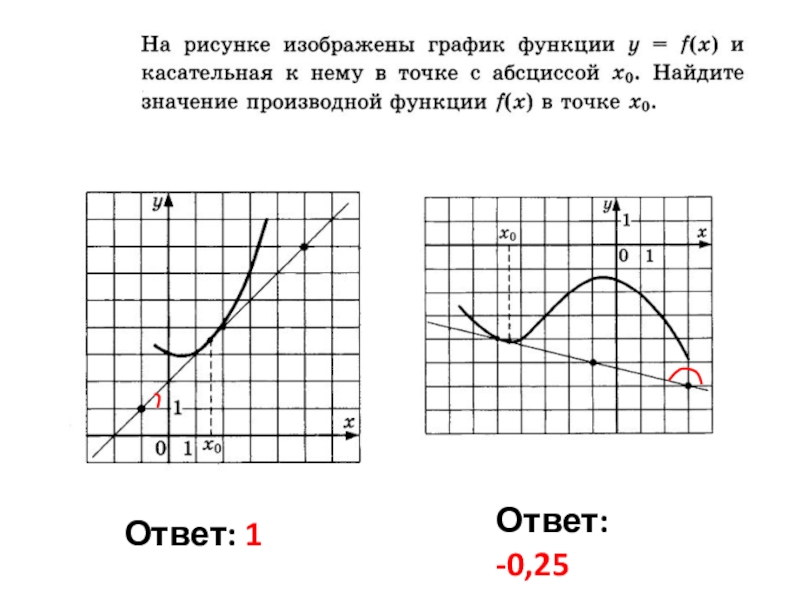
- 10. Ответ: 1Ответ: -0,25
- 11. Монотонность функцииДостаточные признаки монотонности функции. Если f
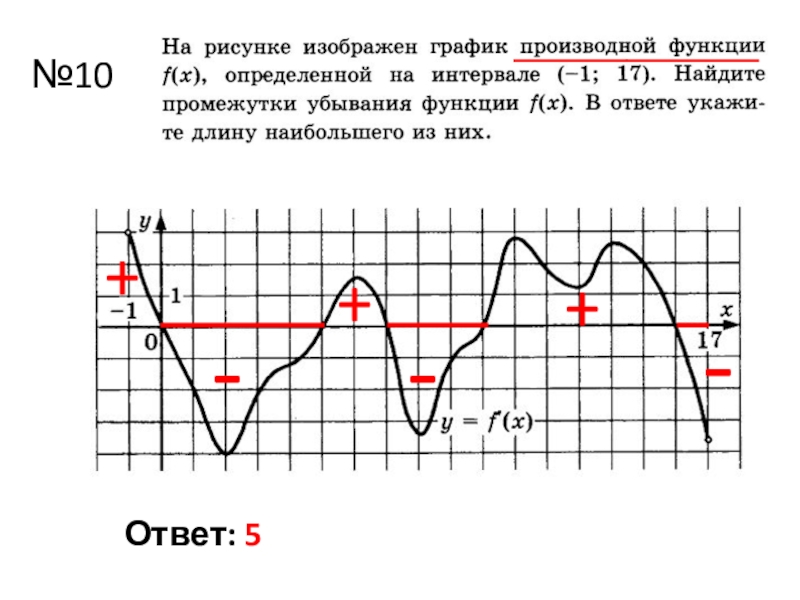
- 12. №10Ответ: 5
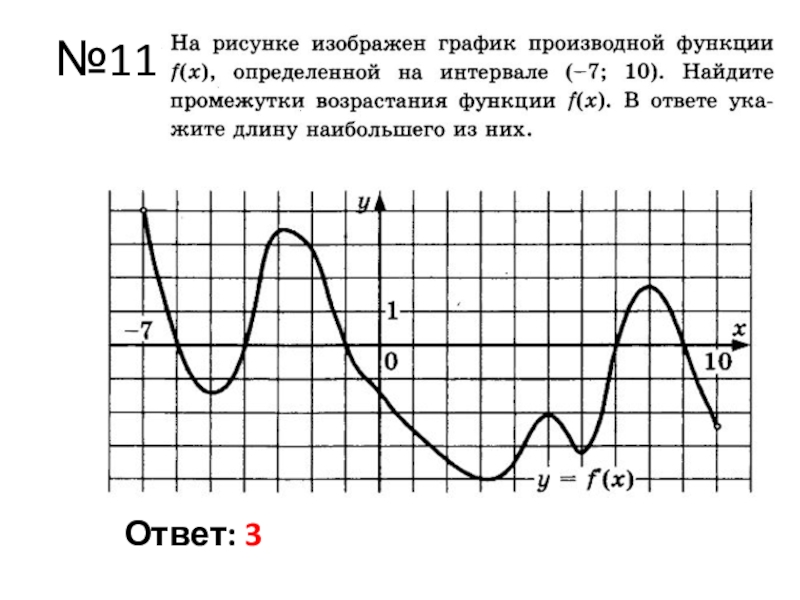
- 13. №11Ответ: 3
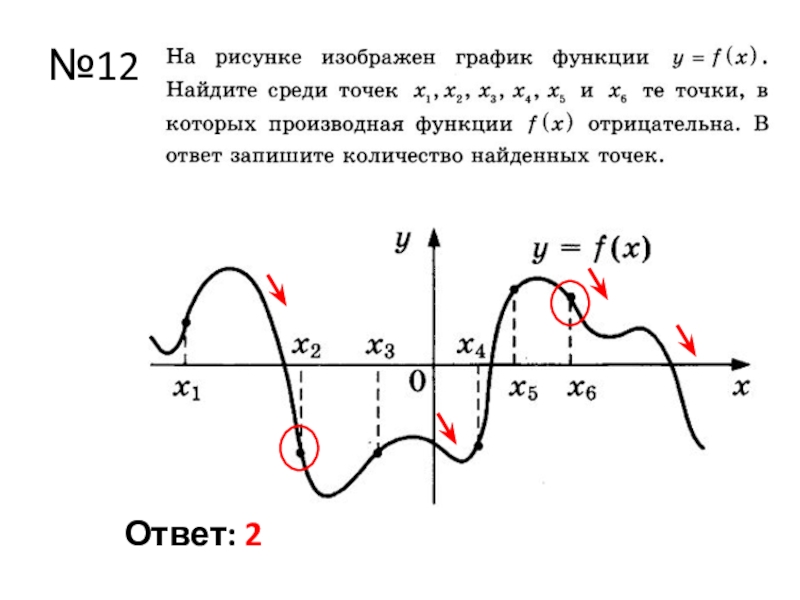
- 14. №12Ответ: 2
- 15. Точки экстремумаТочки минимума и максимума называются точками
- 16. Свойство точек экстремумаВ точках экстремума происходит изменение характера монотонности функции.В точках экстремума производная функции равна нулю.
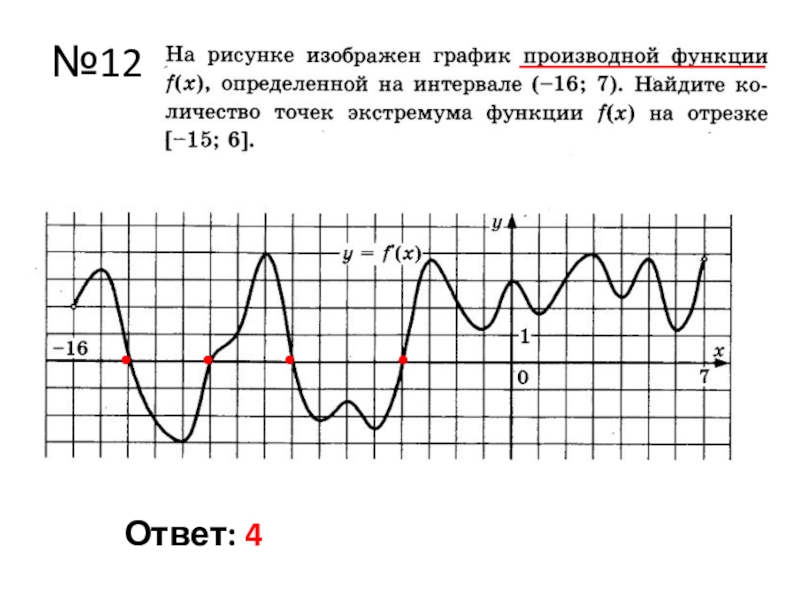
- 17. №12Ответ: 4
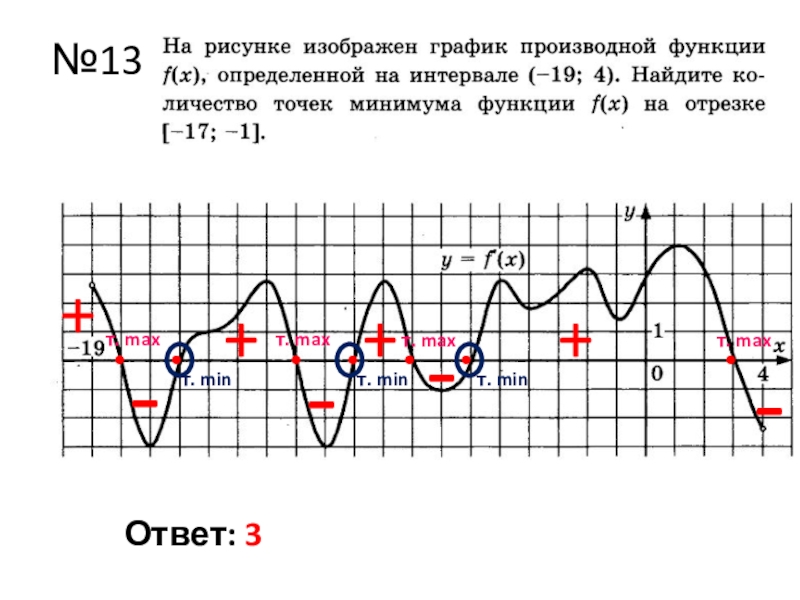
- 18. №13т. minт. minт. minОтвет: 3
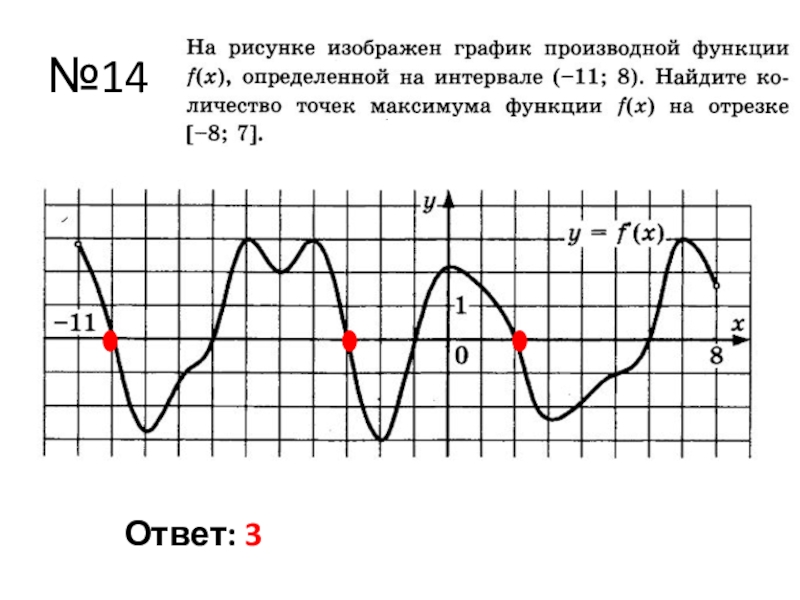
- 19. №14Ответ: 3
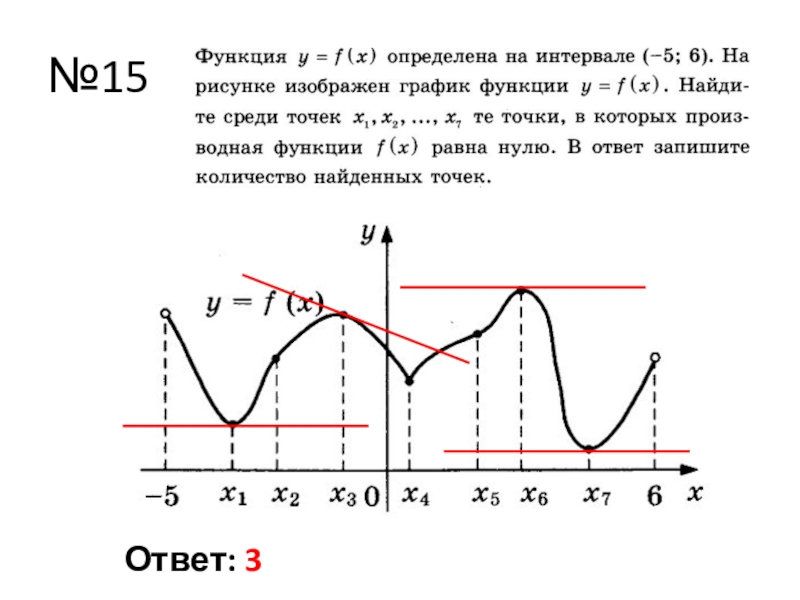
- 20. №15Ответ: 3
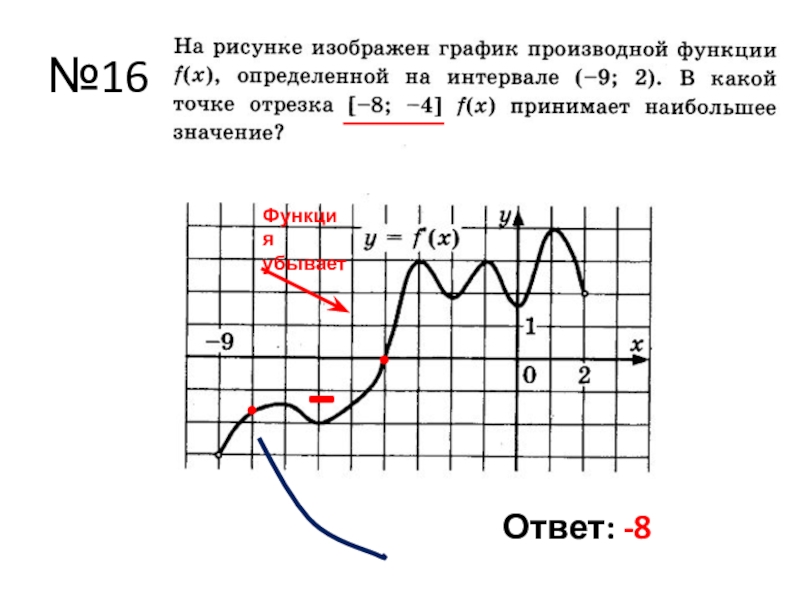
- 21. №16 - ФункцияубываетОтвет: -8
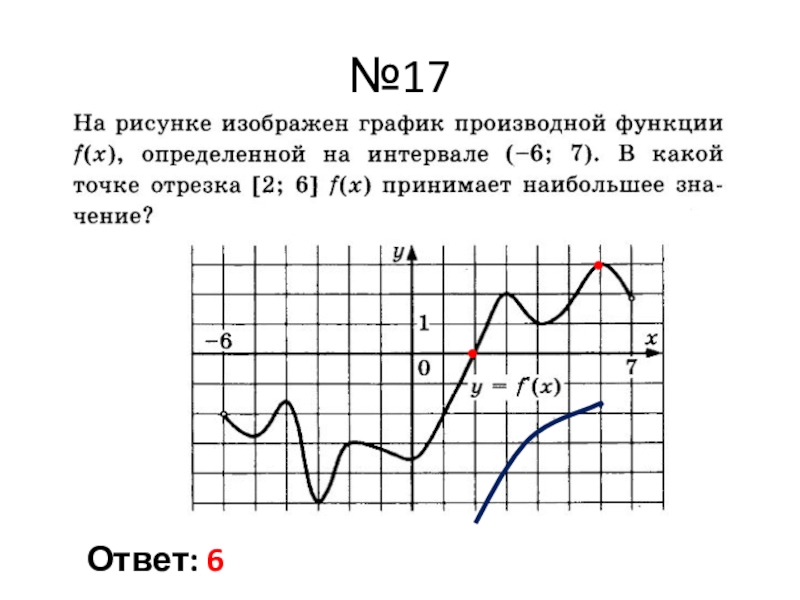
- 22. №17Ответ: 6
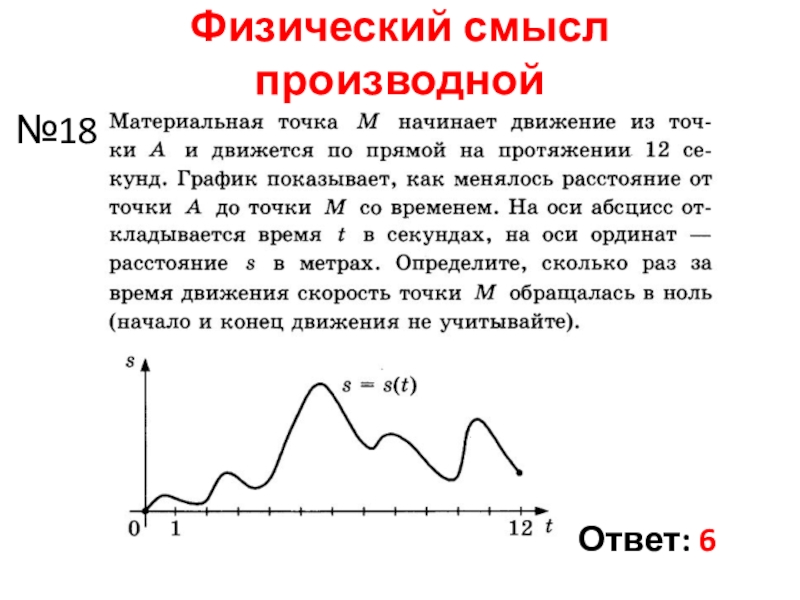
- 23. Физический смысл производнойОтвет: 6№18
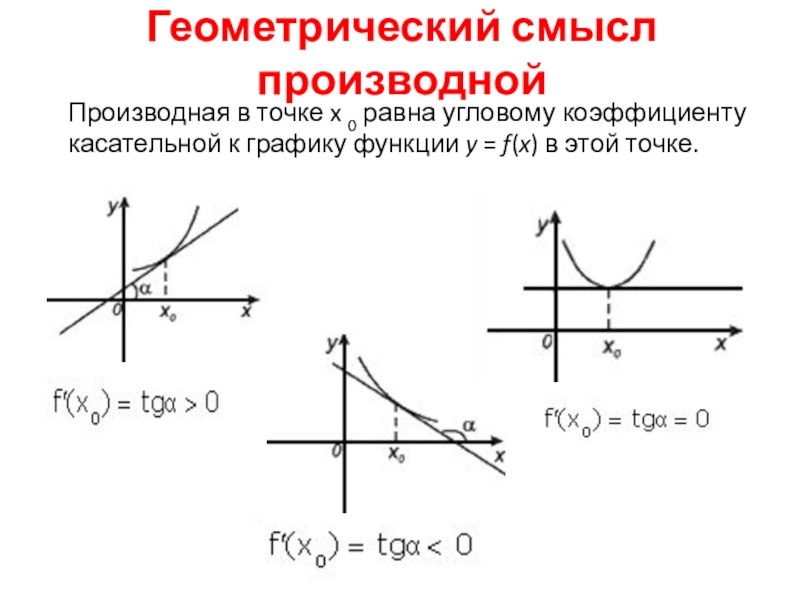
Геометрический смысл производнойПроизводная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Слайд 2Геометрический смысл производной
Производная в точке x 0 равна угловому коэффициенту касательной
к графику функции y = f(x) в этой точке.
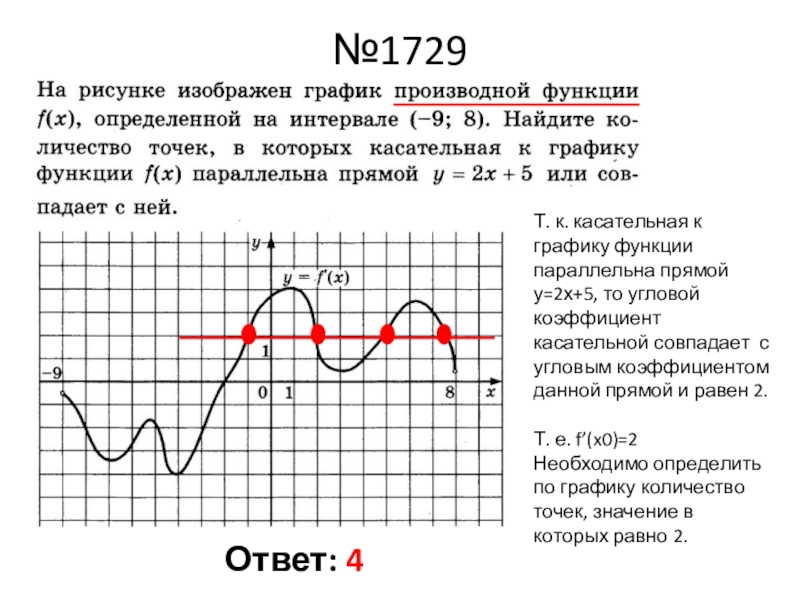
Слайд 5№1729
Т. к. касательная к графику функции параллельна прямой у=2х+5, то угловой
коэффициент касательной совпадает с угловым коэффициентом данной прямой и равен 2.
Т. е. f’(x0)=2
Необходимо определить по графику количество точек, значение в которых равно 2.
Т. е. f’(x0)=2
Необходимо определить по графику количество точек, значение в которых равно 2.
Ответ: 4
Слайд 7№1735
Т. к. касательная к графику функции параллельна прямой у=5, то угловой
коэффициент касательной совпадает с угловым коэффициентом данной прямой и равен 0.
Необходимо определить по графику количество точек, в которых можно построить касательные к графику функции параллельно оси Ох
Необходимо определить по графику количество точек, в которых можно построить касательные к графику функции параллельно оси Ох
Ответ: 7
Слайд 11Монотонность функции
Достаточные признаки монотонности функции.
Если f ’( x ) >
0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Слайд 15Точки экстремума
Точки минимума и максимума называются точками экстремума.
Значение функции в точке
экстремума называется экстремумом функции.
Экстремумом функции называют наибольшее или наименьшее значение функции (еще одно название – максимум или минимум функции)
Экстремумом функции называют наибольшее или наименьшее значение функции (еще одно название – максимум или минимум функции)
Слайд 16Свойство точек экстремума
В точках экстремума происходит изменение характера монотонности функции.
В точках
экстремума производная функции равна нулю.