- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи с параметрами
Содержание
- 1. Презентация по математике на тему Задачи с параметрами
- 2. Некоторые методы решения задач с параметрами1.Аналитический метод.2.Функциональный
- 3. 1. Аналитический метод. Является не
- 4. В аналитическом методе решения задач чаще всего
- 5. Функциональный метод решения задач с параметрамиСвойства функций,
- 6. Графический метод решения задач с параметрами Любая
- 7. Метод заменыМетод замены заключается в формулировке исходного
- 8. Метод изменения ролей переменныхДостаточно часто бывает необходимым
- 9. Метод перехода от общего к частномуЕсли какое-либо
- 10. Метод свободных ассоциацийМетод свободных ассоциаций основан на
- 11. Метод обратного ходаНедостаток условий, выражающийся в том,
- 12. Комбинированные методыКомбинированные методы основаны, как правило, на
- 13. Определение.Решить уравнение или неравенство с параметрами –
- 14. Решить уравнение ах = 3 при всех
- 15. Решить уравнение ах – а2=4-2х.Выполним равносильные преобразования,
- 16. Решить неравенствоДопустимые значения параметра m ≠ 0.Данное неравенство равносильно неравенствам
- 17. 1) Если m=1/2, неравенство примет вид 0∙х>2/3.
- 18. Найти значение параметра а, при которых система
- 19. При каких значениях параметра а уравнение х2
- 20. Решить уравнение x2-4abx – (a2 +
- 21. Найти все значения параметра, при каждом из
- 22. Найти все значения а, при каждом из
- 23. Решить уравнение При х≥0, а ≥1 исходное
- 24. Решить неравенствоПри а≤0 неравенство не имеет решений.При
- 25. Решить неравенство
- 26. Слайд 26
- 27. Решить уравнение 9x+9a(1-a) 3x-2 – a3=0Пусть 3х=t,
- 28. Найти все значения а, при которых уравнение
- 29. Найти все значения а, при которых имеет
- 30. Найти все значения а, при которых имеет
- 31. Решение уравнений с параметром координатным методомПусть
- 32. 2) Параметр а есть функция координаты х:
- 33. Решить уравнение (а2-1)х = 2а2+а-3
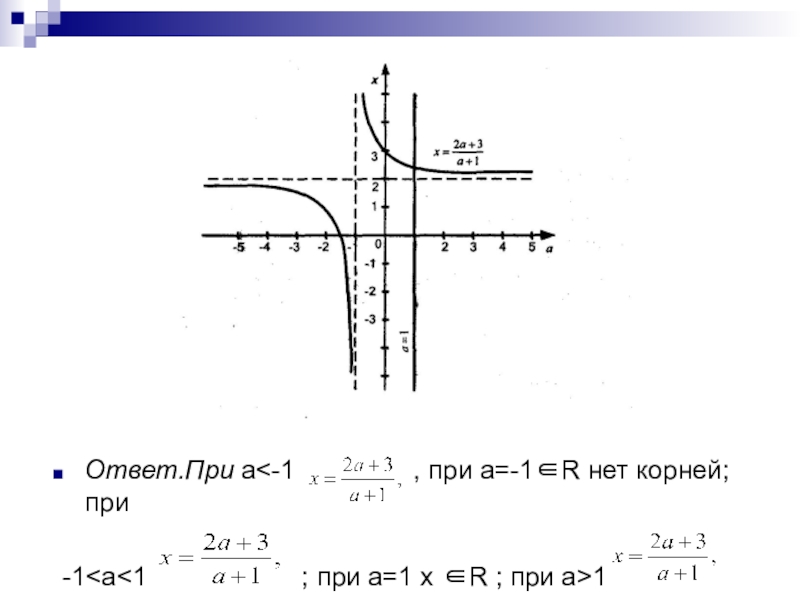
- 34. Ответ.При а
- 35. Найти все значения параметра а, при которых
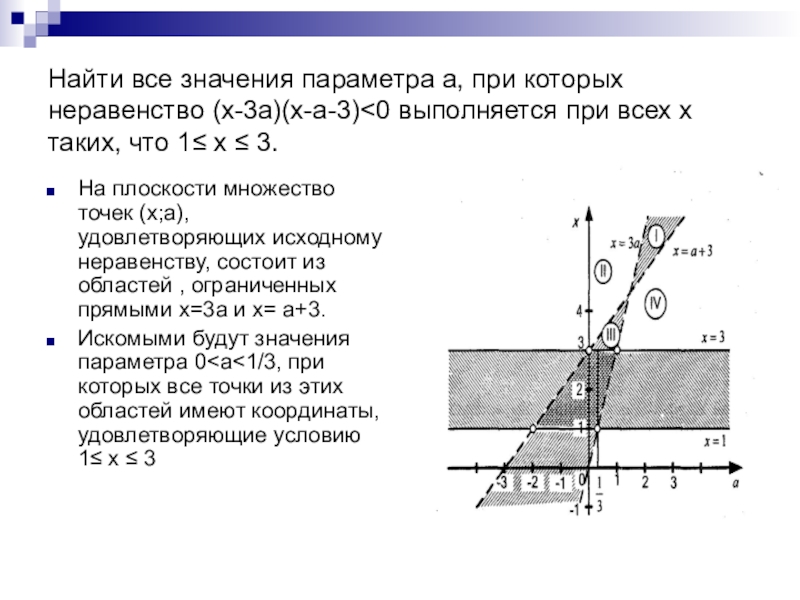
- 36. Найти все значения параметра а, при которых неравенство (х-3а)(х-а-3)
Слайд 2Некоторые методы решения задач с параметрами
1.Аналитический метод.
2.Функциональный метод.
3.Графический метод.
4.Метод замены.
5.Метод изменения
6.Метод перехода от общего к частному.
7.Метод свободных ассоциаций.
8.Метод «обратного хода».
9.Комбинированные методы.
Слайд 31. Аналитический метод.
Является не только самостоятельным методом решения
Слайд 4
В аналитическом методе решения задач чаще всего используется прием дробления —
Так, условие задачи, содержащее выражения, стоящее под знаками модуля, обычно разделяют на совокупность более простых условий, не содержащих модуль.
Слайд 5Функциональный метод решения задач с параметрами
Свойства функций, наиболее часто используемые при
1. кусочная монотонность большинства алгебраических и элементарных трансцендентных функций;
2. свойства четности и нечетности, периодичность функции;
3. свойства ограниченности области определения или области значения функции;
4. при неявном задания функции используются свойства симметрии графика соответствия относительно осей координат или начала координат и т.д.;
5. наиболее часто при решении задач этим методом применяются методы математического анализа: использование непрерывности, дифференцируемости, монотонности, устанавливаемой с помощью тех же методов.
Слайд 6Графический метод решения задач с параметрами
Любая задача с параметрами есть задача
Координатно-графический метод представляет искомые решения в виде геометрического места точек на координатной плоскости, где в качестве одной из координат выступает параметр, а в качестве другой — искомая переменная. Решение задачи в этом случае рассматривается как значение координаты, соответствующей искомой переменной, принадлежащей линии или области, задаваемой условием.
Слайд 7Метод замены
Метод замены заключается в формулировке исходного условия задачи в терминах
Чаще всего метод замены используется при решении тригонометрических уравнений или неравенств. Он позволяет сводить их к алгебраическим уравнениям и неравенствам, анализ которых проще. Однако существуют алгебраические задачи, решение которых становится более простым после получения их тригонометрического эквивалента.
Слайд 8Метод изменения ролей переменных
Достаточно часто бывает необходимым поменять роли искомой переменной
Достаточно часто бывает, что степень искомой переменной гораздо выше, чем степень входящего в условие параметра. Изменение ролей в этом случае приводит к реальному упрощению процесса решения.
Слайд 9Метод перехода от общего к частному
Если какое-либо утверждение в условии задачи
Слайд 10Метод свободных ассоциаций
Метод свободных ассоциаций основан на представлении условия задачи в
В процессе зарождения ассоциаций устанавливаются неординарные взаимосвязи между компонентами решаемой проблемы и элементами внешнего мира. В результате процесса зарождения новых ассоциативных связей и возникают творческие идеи решения проблемы.
Часто используют прием аналогии — поиск аналога и использование всех процедур решения по аналогии, использование результатов аналогичных задач как некоторой базы для решения данной задачи.
Слайд 11Метод обратного хода
Недостаток условий, выражающийся в том, что уравнений или неравенств
Слайд 12Комбинированные методы
Комбинированные методы основаны, как правило, на особых свойствах той или
Слайд 13Определение.
Решить уравнение или неравенство с параметрами – это значит определить ,
1) имеет решение,
2) не имеет решения,
3) установить количество решений,
4) найти вид каждого решения при соответствующих ему значениях параметров.
Слайд 14Решить уравнение ах = 3 при всех значениях параметра а.
Схема анализа
1.Уравнение имеет смысл при любых значениях параметра.
2.Если а≠0, то уравнение имеет единственное решение х= 3/a.
3. Если а=0, то равенство 0∙х=3 невозможно ни при каких значениях переменной х, следовательно, уравнение решений не имеет.
Ответ. При а≠0 решением является число 3/а.
При а=0 уравнение решений не имеет.
Слайд 15Решить уравнение ах – а2=4-2х.
Выполним равносильные преобразования, получим ах – а2=4-2х
1.Если а+2 ≠0, а ≠-2, то , х=2-а.
2. Если а=-2, то уравнение обращается в равенство 0∙ х=0, где х- любое действительное число.
Ответ. Если а ≠-2, то х=2-а.
Если а=0, то решение - любое действительное число.
Слайд 16Решить неравенство
Допустимые значения параметра m ≠ 0.
Данное неравенство равносильно неравенствам
Слайд 17
1) Если m=1/2, неравенство примет вид 0∙х>2/3. Его решением не может
2) Если , т.е. 0 < m <1/2, получим, что
3) Если , что равносильно тому что ,
то
Ответ. При m=1/2 решений нет.
При 0< m <1/2
При m < 0 и m > 1/2
Слайд 18Найти значение параметра а, при которых система
Искомые значение параметра
задаются неравенством 6а2-1≠0. Следовательно,
Ответ. При любом а ≠
Слайд 19При каких значениях параметра а уравнение х2 + ах + 1
Уравнение имеет единственное решение, если дискриминант равен 0.
Следовательно, искомое значение параметра а задается уравнением
а2-4=0, т.е. а = ± 2.
Ответ. -2, 2.
Слайд 20Решить уравнение x2-4abx – (a2 + b2)2=0
1) Здесь D/4 =
2) Если а2≠b2, то D < 0, и уравнение решения не имеет.
3) Если а2=b2, т.е. а = ± b, то уравнение имеет решение , но при этом D = 0, и поэтому единственное значение переменной х, удовлетворяющее уравнению, определяется по формулу х = 2ab.
Ответ.1) Если а2≠b2, то уравнение не имеет корней.
2) Если а2=b2 , то единственный корень х = 2ab.
Слайд 21Найти все значения параметра, при каждом из которых уравнение х2+(3-2а)х -3а+2
По условию, если х1, х2 –корни уравнения, то x1
Получим
Ответ.
Слайд 22Найти все значения а, при каждом из которых неравенство
Х2-х+1 >0 при любых значениях х. Следовательно, 2-ах-х2≤ 3х2-3х+3 ⇔ 4х2+ (а-3)х+1≥ 0.
Так как старший коэффициент положителен, то этот трехчлен будет принимать неотрицательные значения тогда и только тогда, когда D ≤ 0.
D = (а-3)2-16 = (а-7)(а+1).
(а-7)(а+1) ≤ 0 ⇔ -1 ≤ а ≤ 7.
Ответ. [-1;7].
Слайд 23Решить уравнение
При х≥0, а ≥1 исходное уравнение равносильно следующему х2+2х-(а-1)2=0.
Отсюда
где х1< x2.
Ответ.
При а ≥1 уравнение имеет корень х2=-1+
При а<0 корней нет.
Слайд 24Решить неравенство
При а≤0 неравенство не имеет решений.
При а>0 исходное неравенство равносильно
Откуда имеем а ≤ х < a2+a.
Ответ. При а≤0 решений нет;
при а>0 x∈[a;a²+a).
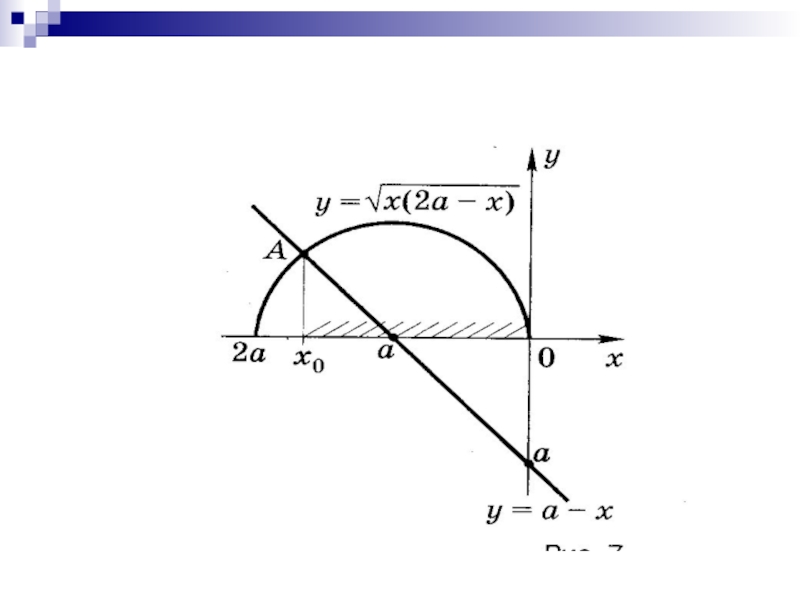
Слайд 25Решить неравенство
Построим эскизы графиков функций
и у=а-х, где а<0 (при а=0 неравенство имеет единственное решение х=0).
Точка пересечения графиков имеет абсциссу – корень уравнения 2ах-х2=(а-х)2 такой, что 2a
Корни
Тогда х0 =х2, а множество решений неравенства - отрезок
Слайд 27Решить уравнение 9x+9a(1-a) 3x-2 – a3=0
Пусть 3х=t, тогда t2+a(1-a)t-a3=0, откуда
Если а=0,
Если а≠0, то t1=a2, t2=-a,
3x=a2, 3x=-a.
Если а>0, то x=log3a2 (3x=-a при а>0 не имеет корней).
Если а=-1, то t=1, т.е. 3х=1 и х=0.
Пусть а<0 и a ≠-1, тогда t1=a2, t2=-a и x1 =log3a2 , х2=log3(-a).
Ответ. При а=0 корней нет.
При а>0 x=log3a2 ;
при а<0 и a ≠-1 x1 =log3a2,х2=log3(-a);
при а=-1 х=0.
Слайд 28Найти все значения а, при которых уравнение
Исходное уравнение равносильно каждой из следующих систем:
Квадратное уравнение системы х2+(2-а)х+1=0 имеет единственный корень, если : 1) D=0, откуда а=0 и а=4, но системе удовлетворяет а=4;
2) D>0 при a<0, a>4, и только один из корней удовлетворяет системе; это верно при a<0.
Ответ. При а=4 и а<0
Слайд 29Найти все значения а, при которых имеет решение уравнение a sinx+(1+a)cosx=
Применим метод вспомогательного угла.
Обозначим
Разделим обе части на b≠0, получим
или
Уравнение имеет решение тогда и только тогда, когда
Ответ. При а≤ -2 , а ≥ 1.
Слайд 30Найти все значения а, при которых имеет корни уравнение sin6x +
Преобразуем левую часть исходного уравнения, получим
Ответ. ¼ ≤ a≤ 1.
Слайд 31Решение уравнений с параметром координатным методом
Пусть F(x,a)=0 некоторая функция переменной
Зададим координатную плоскость хОа. Отметим два частных случая.
1) Координата х есть функция параметра а: x= f(a).
На координатной плоскости хОа горизонтальная ось Оа соответствует значениям параметра а.
Точки (а;х) удовлетворяют уравнению F(x,a)=0 и множество этих точек представляет график функции x= f(a), где роль аргумента играет параметр.
Слайд 32
2) Параметр а есть функция координаты х: а = ϕ (х),
Можно рассматривать плоскость хОа с вертикальной параметрической осью Оа.
Множество всех точек, значения координаты и параметры каждой из которых удовлетворяют уравнению F(x,a)=0 можно интерпретировать как график функции а = ϕ (х), где роль аргумента функции играет координата х.
Центральное место в этом методе занимает нахождение множества всех точек плоскости, определяемых уравнением F(x,a)=0.
Слайд 33Решить уравнение (а2-1)х = 2а2+а-3 относительно х
Данное уравнение
(а-1)(а+1)х = (а-1)(2а+3), и х можно выразить так при условии, что а ≠ 1, а ≠ -1.
Если а=-1, то уравнение корней не имеет.
Если а = 1, то корнем уравнения может быть любое действительное число.
На плоскости хОа множество точек, значения координаты и параметра которых удовлетворяют исходному уравнению, состоит
из гиперболы или и прямой а = 1.
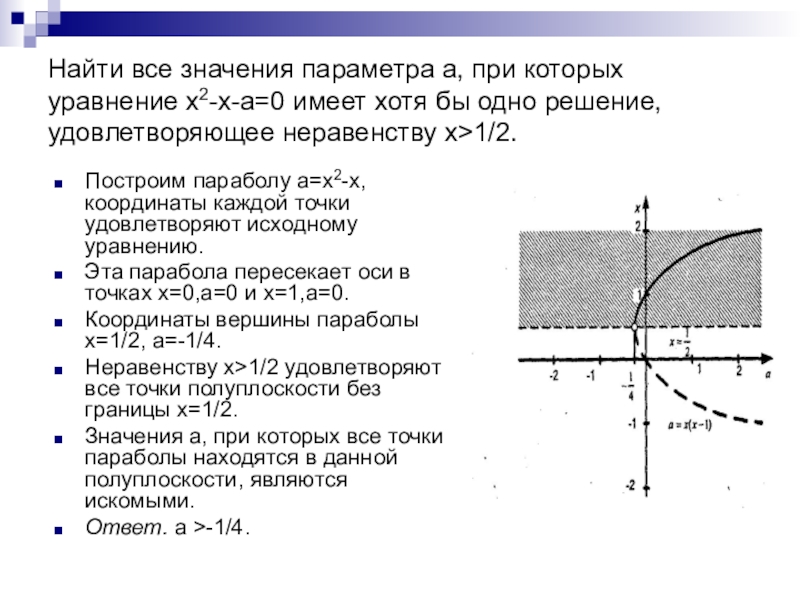
Слайд 35Найти все значения параметра а, при которых уравнение х2-х-а=0 имеет хотя
Построим параболу а=х2-х, координаты каждой точки удовлетворяют исходному уравнению.
Эта парабола пересекает оси в точках х=0,а=0 и х=1,а=0.
Координаты вершины параболы х=1/2, a=-1/4.
Неравенству х>1/2 удовлетворяют все точки полуплоскости без границы х=1/2.
Значения а, при которых все точки параболы находятся в данной полуплоскости, являются искомыми.
Ответ. a >-1/4.
Слайд 36Найти все значения параметра а, при которых неравенство (х-3а)(х-а-3)
На плоскости множество точек (х;а), удовлетворяющих исходному неравенству, состоит из областей , ограниченных прямыми х=3а и х= а+3.
Искомыми будут значения параметра 0