- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Вероятность события
Содержание
- 1. Презентация по математике на тему: Вероятность события
- 2. ЦЕЛИ: разобрать основополагающее понятие теории вероятности;
- 3. СОБЫТИЕ Под СОБЫТИЕМ понимается
- 4. Подбрасывание кубика. Испытание – подбрасывание
- 5. Выбор перчаток. В коробке лежат
- 6. Типы событийДОСТОВЕРНОЕНЕВОЗМОЖНОЕСЛУЧАЙНОЕ
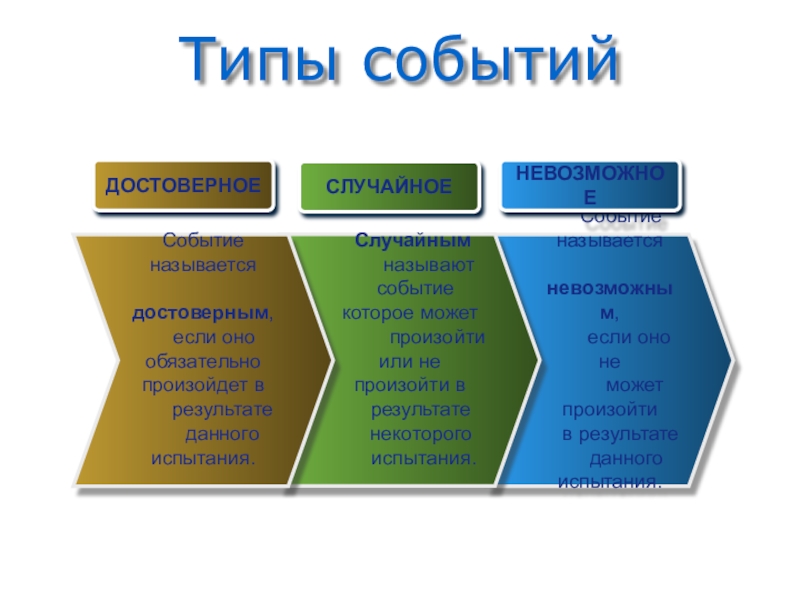
- 7. Типы событий Событие называется
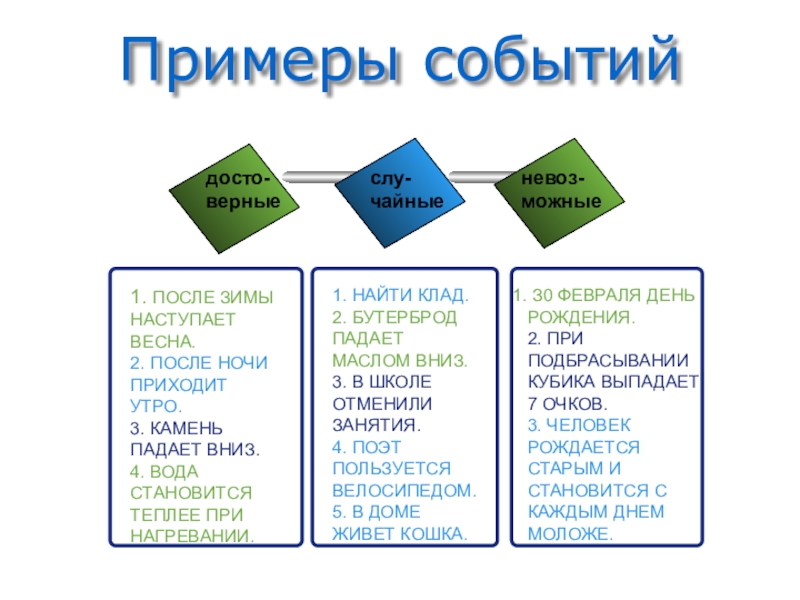
- 8. Примеры событийдосто-верныеслу-чайныеневоз-можные1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.2. ПОСЛЕ
- 9. Охарактеризуйте события, о которых идет речь в
- 10. ИСХОД ИСХОДОМ (или элементарным исходом,
- 11. Число возможных исходов в каждом из рассмотренных
- 12. Запишите множество исходов для следующего испытания.В урне
- 13. Типы событий
- 14. Типы событий
- 15. Действия над событиями
- 16. Действия над событиями
- 17. Действия над событиями
- 18. В толковом словаре С.И. Ожегова и Н.Ю.
- 19. Вероятностью Р наступления случайного события
- 20. Пьер-Симо́н Лапла́с Классическое определение вероятности было впервые дано в работах французского математика Лапласа.
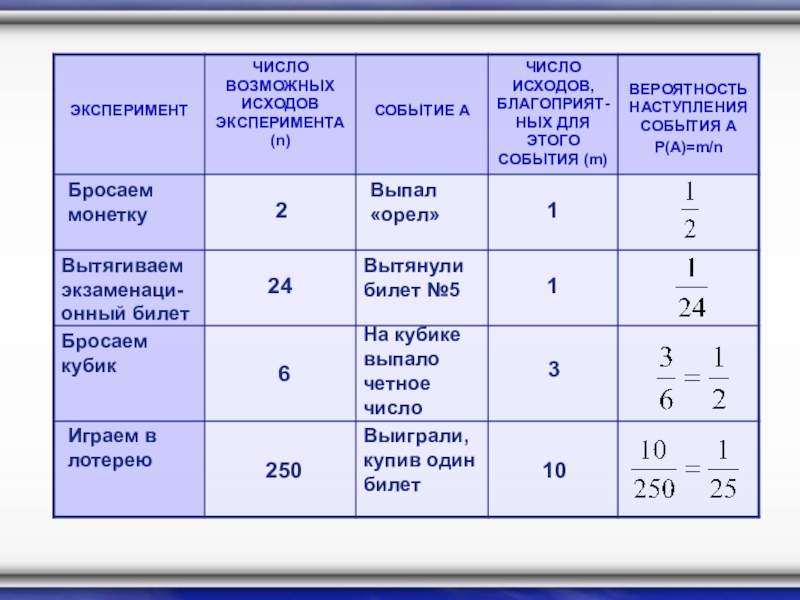
- 21. Бросаем монетку2Выпал «орел»1Вытягиваем экзаменаци- онный билетВытянули билет
- 22. Пример При игре в нарды бросают 2
- 23. Решение Составим следующую таблицуВероятность: P(A)=6/36= =1/6.
- 24. Пример Из карточек составили слово «статистика». Какую
- 25. Всего 10 букв.Буква «с» встречается 2 раза
- 26. Вероятность достоверного события равна Вероятность невозможного события
- 27. P(u) = 1 (u – достоверное событие);P(v)
- 28. Задача 1. В коробке 4 синих, 3
- 29. а) Мы имеем всевозможных случаев 9. Благоприятствующих
- 30. Задача 2. В коробке лежат 10 одинаковых
- 31. Всевозможных событий 6 (красный №1 - красный
- 32. Задача 1. В урне находятся 3 синих,
Слайд 1.
Преподаватель математики Курочкина В.М
Урок на тему:
«ВЕРОЯТНОСТЬ СОБЫТИЯ»
ГБПОУ РМ «Рузаевский
Слайд 2ЦЕЛИ:
разобрать основополагающее понятие теории вероятности;
рассмотреть примеры, поясняющие те или иные события. разобрать понятия классической вероятности;
- рассмотреть свойства вероятности
Слайд 3СОБЫТИЕ
Под СОБЫТИЕМ понимается явление, которое происходит в
ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.
✔
Слайд 4 Подбрасывание кубика.
Испытание – подбрасывание кубика; события – выпало
✔
Слайд 5 Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток.
«Завтра днем – ясная погода».
Здесь наступление дня – испытание, ясная погода – событие.
✔
✔
Слайд 7Типы событий
Событие называется
невозможным,
может произойти
в результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
Слайд 8Примеры событий
досто-
верные
слу-
чайные
невоз-
можные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
3. КАМЕНЬ
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ.
1. НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.
З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.
Слайд 9Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные,
Петя задумал натуральное число. Событие состоит в следующем:
а) задумано четное число;
б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
Задание 1
Слайд 10ИСХОД
ИСХОДОМ (или элементарным исходом, элементарным событием) называется один
✔
Слайд 11Число возможных исходов в каждом из рассмотренных выше опытах.
1. – 2
– 6 исходов: 1, 2, 3, 4, 5, 6.
– 3 исхода: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки».
✔
✔
✔
Слайд 12Запишите множество исходов для следующего испытания.
В урне четыре шара с номерами
.
Задание
Слайд 13Типы событий
||
Например, событие А – «выпало четное число очков» и B – «выпало нечетное число очков» при бросании игрального кубика – противоположные.
Придумайте два противоположных события.
Слайд 14Типы событий
||
Пример. А – «идет дождь», В – «на небе нет ни облачка» – несовместные.
Пример. Коля и Саша играют в шашки. А – «Коля проиграл», В – «Саша выиграл», С – «Витя наблюдал за игрой» – совместные.
Слайд 15Действия над событиями
называется событие, состоящие в
наступлении хотя бы одного из них в
результате испытания.( , )
Если события А и В совместны, то сумма А+В
означает, что наступает событие А, или событие
В, или оба события вместе.
Если события несовместны, то событие А+В
заключается в том, что должны наступить А или
В, тогда + заменяется словом «или». .
Слайд 16Действия над событиями
красные, белые и черные шары.
Вынимается один шар. Возможные
события: А – «вынут красный шар», В –
«вынут белый шар», С – « вынут
черный шар».
Тогда А+В означает, что произошло
событие «вынут не черный шар», В+С –
«вынут не красный шар».
Слайд 17Действия над событиями
называется событие, состоящие в
совместном наступлении всех этих событий в результате испытания.
( ).
Означает союз «и» (АВС, это означает, что
наступило событие А и В и С).
Пример. Пусть имеются следующие события: А – «из колоды карт вынута дама», В – «из колоды карт вынута карта пиковой масти». Значит, А*В означает «вынута дама пик».
Пример. Бросается игральный кубик. Рассмотрим следующие события: А – « число выпавших очков < 5», В – «число выпавших очков > 2», С – «число выпавших очков четное». Тогда А*В*С – «выпало 4 очка».
Слайд 18В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность – возможность исполнения,
Основатель современной теории вероятностей А.Н.Колмогоров:
«Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
Понятие вероятности
Слайд 19 Вероятностью Р наступления случайного события А называется отношение
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Слайд 20
Пьер-Симо́н Лапла́с
Классическое определение вероятности было впервые дано в работах французского
Слайд 21Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем кубик
На кубике выпало
6
3
Играем в лотерею
Выиграли, купив один билет
250
10
Слайд 22Пример
При игре в нарды бросают 2 игральных кубика. Какова вероятность
При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?
Слайд 24
Пример
Из карточек составили слово «статистика». Какую карточку с буквой вероятнее
с
т
а
т
и
с
т
и
к
а
Слайд 25Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10
буква «т» встречается 3 раза –
P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение
Слайд 26Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А
?
1
?
?
?
0
1
0
Свойства вероятности
Слайд 28
Задача 1.
В коробке 4 синих, 3 белых и 2 желтых
Самостоятельная работа
Слайд 29
а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:
P=3:9=1/3=0,33(3)
б)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
Решение
Слайд 30
Задача 2.
В коробке лежат 10 одинаковых шаров, на каждом из
Слайд 31
Всевозможных событий 6 (красный №1 - красный №2; красный №1 -
Решение
Слайд 32
Задача 1. В урне находятся 3 синих, 8 красных и 9
Задача 2. Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а Лена – билет, который участвует в розыгрыше трех призов на 70000. У кого больше шансов выиграть?
Домашнее задание